这是Lecture 10 – Convolutional Networks,Lecture 14 – Implementing Convolutions的笔记。
Convolutions in detail
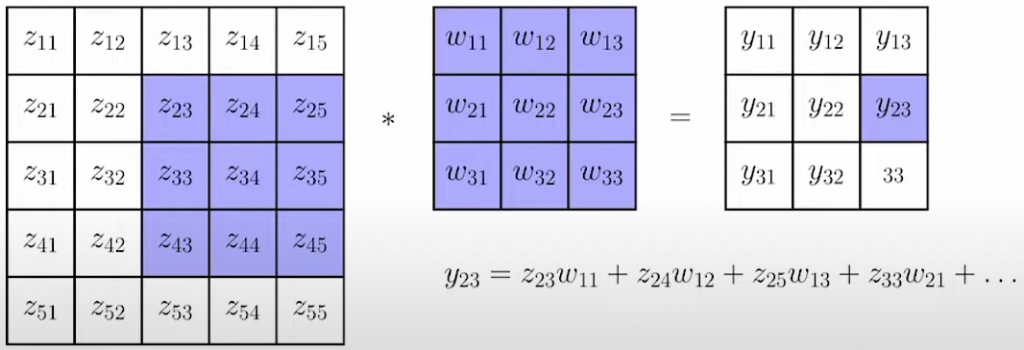
在DL中,卷积实际上就是指在原图 $z$ 上“滑动”一个卷积核 $w$,并进行逐元素乘法。如上图所示,即
$$
y = z * w
$$
DL中的卷积并不需要翻转卷积核,让卷积运算变成最常见的
$$
h_k=\sum_{i+j=k} f_i\cdot g_j
$$
形式。
Multi-channel convolutions
卷积最常见的应用场景就是二维图像提取特征图,但是二维图像往往不只有一个通道(e.g., RGB),因此卷积最常见的应用场景是多通道卷积,例如
- $x\in\mathbb R^{h\times w\times c_{in}}$
- $z\in\mathbb R^{h\times w\times c_{out}}$
- $W\in\mathbb R^{c_{in}\times c_{out}{\times} k\times k}$
这里 $x$ 表示输入图像,$c_{in}$ 表示输入通道数;$z$ 表示输出的特征图,$c_{out}$ 表示输出通道数;$W$ 表示多通道卷积核。
多通道卷积的运算公式如下(1-index)
$$
z[:,:,s] = \sum_{r=1}^{c_{in}} x[:,:,r] * W[r,s,:,:]
$$
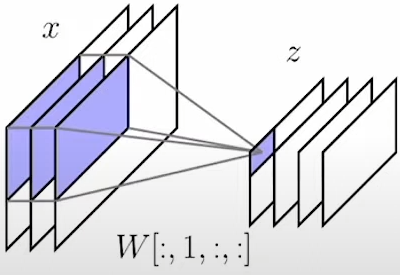
以上图为例,输出 $z$ 的第一个通道是由输入 $x$ 的所有通道分别与 $W[:,1,:,:]$ 中的卷积核点乘,然后加权得到的,也就是
$$
z[:,:,1] = x[:,:,1]*W[1,1,:,:] + x[:,:,2]*W[2,1,:,:] + x[:,:,3]*W[3,1,:,:]
$$
因此一个 $c_{in}$ 到 $c_{out}$ 的多通道卷积实际上有 $c_{in}\times c_{out}$ 个卷积核,总参数量为 ${c_{in}\times c_{out}{\times} k\times k}$。
思考多通道卷积更合理的思路是从向量的角度来看,对于输入 $x\in\mathbb R^{h\times w\times c_{in}}$,我们可以认为 $x$ 是由 $h\times w$ 个长度为 $c_{in}$ 的一维向量构成的,$z$ 是由 $h\times w$ 个长度为 $c_{out}$ 的向量构成的,也就是
$$
\begin{aligned}
\textbf{x}_{i,j}& = \pmatrix{x_{i,j,1} & x_{i,j,2} & \cdots & x_{i,j,c_{in}}}\\
\textbf{z}_{i,j}& = \pmatrix{z_{i,j,1} & z_{i,j,2} & \cdots & z_{i,j,c_{out}}}\\
\end{aligned}
$$
此时,卷积核 $W$ 应该被视作矩阵乘法运算,令输入的一维向量维度从 $c_{in}$ 变成 $c_{out}$,也就是说 $\textbf W\in\mathbb{V}^{k\times k}$,$\textbf{W}_{i,j}\in\mathbb R^{c_{in}\times c_{out}}$,(这里 $\mathbb V$ 表示二维向量空间,每个向量都是 $c_{in}\times c_{out}$ 的size)于是卷积就变成了矩阵向量积。相当于做了 $h\times w$ 次矩阵乘法,每次矩阵乘法是 $1\times c_{in}$ 和 $c_{in}\times c_{out}$ 两个矩阵相乘。

Implementation
torch
首先规定卷积 $z=\text{conv}(x,W)$ 代码实现的通道:
- $x$ 的shape为 $(N, H, W, C)$。这里 $N$ 表示batch size,$C$ 表示输入通道数。
- $W$ 的shape为 $(K,K,C_{in},C_{out})$。这里的 $C_{in}$ 和上面的 $C$ 是一样的。
但是,根据pytorch的通道定义,如果我们要调用torch的二维卷积api,就需要转换通道为
- $x:(N,C,H,W)$
- $W:(C_{out},C_{in},K,K)$
因此可以得到torch版本的卷积前向传播实现:
import torch
import torch.nn.functional as F
import numpy as np
def conv_conference(x, W):
x_torch = torch.from_numpy(x)
x_torch = x_torch.permute(0, 3, 1, 2) # NCinHW
W_torch = torch.from_numpy(W)
W_torch = W_torch.permute(3, 2, 0, 1) # OIKK
out = F.conv2d(x_torch, W_torch) # NCoutHW
return out.permute(0, 2, 3, 1).contiguous().numpy() # NHWCout
np.random.seed(58)
x = np.random.randn(10, 32, 32, 8) # N, H, W, C
W = np.random.randn(3, 3, 8, 16) # K, K, Cin, Cout
z1 = conv_conference(x, W)Naive
def conv_naive(x, weight):
N, H, W, Cin = x.shape
K, _, _, Cout = weight.shape
out = np.zeros((N, H - K + 1, W - K + 1, Cout))
for n in range(N):
for c_in in range(Cin):
for c_out in range(Cout):
for h in range(H - K + 1):
for w in range(W - K + 1):
for i in range(K):
for j in range(K):
out[n, h, w, c_out] += weight[i, j, c_in, c_out] * x[n, h + i, w + j, c_in]
return out
z2 = conv_naive(x, W)
print(np.linalg.norm(z1 - z2))最简单的卷积实现方法就是暴力for循环,也就是7个for loop。容易发现,这个代码跑得非常慢。
输出 1.2229212744312099e-12,属于精度误差。
Matrix-Vetor Product
更好一点的方法就是将卷积运算视作矩阵向量积,注意这里的代码相较于前文的描述多了一个通道(batch size),此外还需要额外处理二维卷积后缩水的 $h\times w$。
def conv_matmul(Z, weight):
N, H, W, Cin = Z.shape
K, _, _, Cout = weight.shape
out = np.zeros((N, H - K + 1, W - K + 1, Cout))
for i in range(K):
for j in range(K):
out += Z[:, i:i + H - K + 1, j:j + W - K + 1, :] @ weight[i, j] # 无padding的二维卷积
return out
z3 = conv_matmul(x, W)
print(np.linalg.norm(z3 - z1))Gradient
定义卷积运算为
$$
z = \text{conv}(x,W)
$$
我们怎么计算 $\frac{\partial z}{\partial x}, \frac{\partial z}{\partial W}$ 呢?
Review Linear Layer
我们已经知道,计算图本质上是在求雅可比向量积,对于最简单的无bias线性层 $z=Wx$,($x\in\mathbb R^{n},z\in\mathbb R^m,W\in\mathbb R^{n\times m}$)我们需要求出 $\frac{\partial z}{\partial W}$ 来更新参数 $W$,还需要求出 $\frac{\partial z}{\partial x}$ 来回传梯度,具体地
$$
\begin{aligned}
\frac{\partial \ell}{\partial W} &= \frac{\partial \ell}{\partial z}\frac{\partial z}{\partial W}\\
\frac{\partial \ell}{\partial x} &= \frac{\partial \ell}{\partial z}\frac{\partial z}{\partial x}\\
\end{aligned}
$$
而根据线性层的公式 $z=Wx$,很容易求出偏导关系 $z_x=W,z_W=x^T$。
因此这两个偏导数就是
$$
\begin{aligned}
\frac{\partial \ell}{\partial W} &= \frac{\partial \ell}{\partial z}x^T\\
\frac{\partial \ell}{\partial x} &= \frac{\partial \ell}{\partial z}W\\
\end{aligned}
$$
不过由于 $\frac{\partial \ell}{\partial z}$ 的维度通常表示为 $\mathbb R^{m\times 1}$,因此 $\frac{\partial \ell}{\partial x}$ 通常记作 $W^T\frac{\partial \ell}{\partial z}$。
更好的想法就是直接将卷积视作矩阵乘法,那么我们就可以直接用Linear Layer的结论求出梯度了。
举个例子,我们从一维卷积入手,假设输出 $z = \pmatrix{z_1 & z_2 & \cdots & z_5}$,输入 $x = \pmatrix{0 & x_1 & x_2 & \cdots & x_5 & 0}$,也就是进行了0-padding的向量,卷积核是 $w=\pmatrix{w_1&w_2&w_3}$,我们可以将这个卷积很直观地表示为矩阵乘法
$$
\pmatrix{z_1\\ z_2\\ z_3\\ z_4\\ z_5} = Wx=
\pmatrix{
w_2&w_3&0&0&0\\
w_1&w_2&w_3&0&0\\
0&w_1&w_2&w_3&0\\
0&0&w_1&w_2&w_3\\
0&0&0&w_1&w_2
}
\pmatrix{x_1\\ x_2\\x_3\\x_4\\x_5}
$$
于是就有
$$
W^T = \pmatrix{
w_2&w_3&0&0&0\\
w_1&w_2&w_3&0&0\\
0&w_1&w_2&w_3&0\\
0&0&w_1&w_2&w_3\\
0&0&0&w_1&w_2
}^T
$$
我们就把一维卷积用矩阵乘法表示,并用转置表示出了 $W$ 的梯度,即 $\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z}$。
此外,我们还可以改变矩阵乘法的顺序
$$
\pmatrix{z_1\ z_2\ z_3\ z_4\ z_5} = XW =
\pmatrix{
0&x_1&x_2\\
x_1&x_2&x_3\\
x_2&x_3&x_4\\
x_3&x_4&x_5\\
x_4&x_5&0
}
\pmatrix{w_1\ w_2\ w_3}
$$
于是 $\frac{\partial z}{\partial W} = X$,$\frac{\partial \ell}{\partial W} = \frac{\partial \ell}{\partial z}X$。
这个做法显然也可以拓展到二维情况,比如 $x=\pmatrix{x_{1,1}&x_{1,2}&x_{1,3}\\ x_{2,1}&x_{2,2}&x_{2,3}\\ x_{3,1}&x_{3,2}&x_{3,3}}, W=\pmatrix{w_{1,1}&w_{1,2}\ w_{2,1}&w_{2,2}}$,可以表示为
$$
z=\tilde{W}x =
\begin{bmatrix}
w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0&0&0&0\\
0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0&0&0\\
0&0&0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0\\
0&0&0&0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&\\
\end{bmatrix}
\begin{bmatrix}
x_{1,1}\\
x_{1,2}\\
x_{1,3}\\
x_{2,1}\\
x_{2,2}\\
x_{2,3}\\
x_{3,1}\\
x_{3,2}\\
x_{3,3}\\
\end{bmatrix}
$$
或者
$$
X = \begin{bmatrix}
x_{1,1} & x_{1,2} & x_{2,1} & x_{2,2} \\
x_{1,2} & x_{1,3} & x_{2,2} & x_{2,3} \\
x_{2,1} & x_{2,2} & x_{3,1} & x_{3,2} \\
x_{2,2} & x_{2,3} & x_{3,2} & x_{3,3}
\end{bmatrix}, \tilde{W} = \begin{bmatrix}
w_{1,1} \\
w_{1,2} \\
w_{2,1} \\
w_{2,2}
\end{bmatrix}, z = X \tilde{W}
$$
不难发现在卷积核通常较小的情况下,用 $z=XW$ 的形式复杂度较低。
Implementation
im2col
这是对二维卷积前向传播的补充,注意到反向传播中将卷积转化为矩阵乘法的技术实际上也可以应用到卷积的前向传播中,这种技术被称为是im2col(image to column),简单地说,就是将二维卷积核展平为一个列向量,比如上方例子中的 $W=\pmatrix{w_{1,1}&w_{1,2}\\ w_{2,1}&w_{2,2}}\to \tilde{W} = \begin{pmatrix}
w_{1,1} \\
w_{1,2} \\
w_{2,1} \\
w_{2,2}
\end{pmatrix}$。然后卷积就能够通过高效的矩阵乘法运算进行加速。因此,唯一剩下的问题就是怎么高效地将输入的二维图像 $x$ 转化为 $X$。
这里需要用到 as_strided 函数,注意到这里的 $X$ 矩阵中的元素全部来源于 $x$,我们实际上不需要把 $X$ 在内存中去建出来,只需要每次运算时取出所需元素。观察
$$
x=\pmatrix{x_{1,1}&x_{1,2}&x_{1,3}\\ x_{2,1}&x_{2,2}&x_{2,3}\\ x_{3,1}&x_{3,2}&x_{3,3}}, X = \begin{pmatrix}
x_{1,1} & x_{1,2} & x_{2,1} & x_{2,2} \\
x_{1,2} & x_{1,3} & x_{2,2} & x_{2,3} \\
x_{2,1} & x_{2,2} & x_{3,1} & x_{3,2} \\
x_{2,2} & x_{2,3} & x_{3,2} & x_{3,3}
\end{pmatrix}
$$
实际上 $X$ 的每一行就是一个 $2\times 2$ 的滑动窗口作用于 $x$:$\pmatrix{x_{1,1}&x_{1,2}\\ x_{2,1}&x_{2,2}}, \pmatrix{x_{1,2}&x_{1,3}\\ x_{2,2}&x_{2,3}},\pmatrix{x_{2,1}&x_{2,2}\\ x_{3,1}&x_{3,2}},\pmatrix{x_{2,2}&x_{2,3}\\ x_{3,2}&x_{3,3}}$;
而 as_strided 函数的作用就是基于原有的数组,通过shape和stride新建一个视图,比如
a = np.arange(0, 8).reshape(2, 4)
b = np.lib.stride_tricks.as_strided(a, shape=(3, 2, 4), strides=(0, 16, 4))
print(a)
print(b)输出为
[[0 1 2 3]
[4 5 6 7]]
[[[0 1 2 3]
[4 5 6 7]]
[[0 1 2 3]
[4 5 6 7]]
[[0 1 2 3]
[4 5 6 7]]]这里 strides 要除以字节长度 4,也就是步长实际上是 (0, 4, 1)。因为第一个维度的步长是 $0$,所以上方的 as_strided 就相当于是重复遍历了三次原数组 a,但是 b 中的元素是通过步长取出 a 中的元素,并没有发生任何拷贝,具体地,b[x, y, z] = a[x * strides[0] + y * strides[1] + z * strides[2]]。
通过 as_strided 就可以在避免拷贝的情况下生成这个类似于滑动窗口的 $X$ 了,
def conv_im2col(x, weight):
N, H, W, C_in = x.shape
K, _, _, C_out = weight.shape
Ns, Hs, Ws, Cs = x.strides
inner_dim = K * K * C_in
y = np.lib.stride_tricks.as_strided(
x,
shape=(N, H - K + 1, W - K + 1, K, K, C_in),
strides=(Ns, Hs, Ws, Hs, Ws, Cs)
)
y = y.reshape(-1, inner_dim)
out = y @ weight.reshape(-1, C_out)
return out.reshape((N, H - K + 1, W - K + 1, C_out))
z4 = conv_im2col(x, W)
print(np.linalg.norm(z4 - z1))pad, stride, dilate
这一部分是hw4中需要实现的二维卷积前向传播,具体地说需要实现一个相对功能完整的二维卷积,包括 pad, stride, dilate。
class Conv(TensorOp):
def __init__(self, stride: Optional[int] = 1, padding: Optional[int] = 0):
self.stride = stride
self.padding = padding
def compute(self, A, B):
### BEGIN YOUR SOLUTION
# A (N, H, W, C)
# B (K, K, I, O)
if self.padding:
A = A.pad(((0, 0), (self.padding, self.padding), (self.padding, self.padding), (0, 0)))
N, H, W, C_in = A.shape
K, _, _, C_out = B.shape
Ns, Hs, Ws, Cs = A.strides
inner_dim = K * K * C_in
out_H, out_W = (H - K) // self.stride + 1, (W - K) // self.stride + 1
out = A.as_strided(
shape=(N, out_H, out_W, K, K, C_in),
strides=(Ns, Hs * self.stride, Ws * self.stride, Hs, Ws, Cs)
).compact().reshape((N * out_H * out_W, inner_dim))
out = out @ B.reshape((K * K * C_in, C_out))
return out.compact().reshape((N, out_H, out_W, C_out))
### END YOUR SOLUTIONconv中主要需要计算 stride != 1 时的shape,也就是 out_H, out_W = (H - K) // self.stride + 1, (W - K) // self.stride + 1。此外注意这里需要用 compact() 将视图转化为连续的一维数组。
conv中主要需要计算 stride != 1 时的shape,也就是 out_H, out_W = (H - K) // self.stride + 1, (W - K) // self.stride + 1。此外注意这里需要用 compact() 将视图转化为连续的一维数组。
dilate的实现实际上就是先准备一个全0的大数组,然后根据步长将原数组填入这个全0的大数组。一个例子是:
$$
\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}
\Longrightarrow
\begin{bmatrix}
1 & 0 & 2 & 0 \\
0 & 0 & 0 & 0 \\
3 & 0 & 4 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
$$
def dilate(a, axes, dilation):
new_shape = list(a.shape)
for i in axes:
new_shape[i] += a.shape[i] * dilation
canvas = np.zeros(new_shape)
slices = [slice(None) for i in new_shape]
for i in axes:
slices[i] = slice(None, None, dilation + 1)
canvas[tuple(slices)] = a
return canvas
a = np.arange(4).reshape(2, 2)
print(dilate(a, (0, 1), 1))backward
在前文中我们已经说明了二维卷积和矩阵乘法的相互转换,因此梯度的计算可以用矩阵乘法表示为
$$
\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z},\ \frac{\partial \ell}{\partial W} = \frac{\partial \ell}{\partial z}X
$$
注意本章节中 $\frac{\partial \ell}{\partial z}$ 等效于
out_grad。此外,本章节默认 $H=W$。
$\frac{\partial \ell}{\partial x}$
matmul to conv
先讨论 $\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z}$,回顾之前的例子
$$
\pmatrix{z_1\\ z_2\\ z_3\\ z_4\\ z_5} = Wx=
\pmatrix{
w_2&w_3&0&0&0\\
w_1&w_2&w_3&0&0\\
0&w_1&w_2&w_3&0\\
0&0&w_1&w_2&w_3\\
0&0&0&w_1&w_2
}
\pmatrix{x_1\\ x_2\\x_3\\x_4\\x_5}
$$
如果将 $W$ 换为 $W^T$ 就变成了
$$
W^Tx=
\pmatrix{
w_2&w_1&0&0&0\\
w_3&w_2&w_1&0&0\\
0&w_3&w_2&w_1&0\\
0&0&w_3&w_2&w_1\\
0&0&0&w_3&w_2
}
\pmatrix{x_1\\ x_2\\x_3\\x_4\\x_5}
$$
实际上这就是从 $\pmatrix{w_1&w_2&w_3}$ 变成了 $\pmatrix{w_3&w_2&w_1}$ 的卷积(翻转卷积核)。
对于二维卷积,我们只需要两次翻转(水平、垂直),因此
$$
\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z} = \text{conv}(\frac{\partial \ell}{\partial z}, \text{flip}(W))
$$
但是,这里我们忽略了维度的变化,举个简单的二维卷积例子 $x\in\mathbb R^{3\times 3},W\in\mathbb R^{2\times 2}$,此时 $z\in\mathbb R^{2\times 2}$,$\frac{\partial \ell}{\partial x}\in\mathbb R^{2\times 2}$,如果我们直接进行 $\text{conv}(\frac{\partial \ell}{\partial z}, \text{flip}(W))$ 操作,那么维度显然是不对的,因为 $\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z}\in\mathbb R^{9\times 1}$(这里 $\frac{\partial \ell}{\partial z}$ reshape到 $4\times 1$),然后reshape成 $\mathbb R^{3\times 3}$ 才是正确的。
对于这个case,我们把二维卷积展开成矩阵乘法
$$
\begin{aligned}
\frac{\partial \ell}{\partial x}=W^T\frac{\partial \ell}{\partial z} &=
\begin{bmatrix}
w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0&0&0&0\\
0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0&0&0\\
0&0&0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&0\\
0&0&0&0&w_{1,1}&w_{1,2}&0&w_{2,1}&w_{2,2}&\\
\end{bmatrix}^T
\begin{bmatrix}
l_{1,1}\\
l_{1,2}\\
l_{2,1}\\
l_{2,2}\\
\end{bmatrix}\\
&=
\begin{bmatrix}
w_{1,1}l_{1,1}\\
w_{1,2}l_{1,1}+w_{1,1}l_{1,2}\\
w_{1,2}l_{1,2}\\
w_{2,1}l_{1,1}+w_{1,1}l_{2,1}\\
w_{2,2}l_{1,1}+w_{2,1}l_{1,2}+w_{1,2}l_{2,1}+w_{1,1}l_{2,2}\\
w_{2,2}l_{1,2}+w_{1,2}l_{2,2}\\
w_{2,1}l_{2,1}\\
w_{2,2}l_{2,1}+w_{2,1}l_{2,2}\\
w_{2,2}l_{2,2}
\end{bmatrix}
\end{aligned}
$$
这里实际上是翻转后的卷积核 $\pmatrix{w_{2,2}&w_{2,1}\\ w_{1,2}&w_{1,1}}$ 在padding后的 $\pmatrix{0&0&0&0\\ 0&l_{1,1}&l_{1,2}&0\\ 0&l_{2,1}&l_{2,2}&0\\ 0&0&0&0}$ 上滑动,最后求出 $3\times 3$ 的梯度。也就是说 $\text{conv}(\frac{\partial \ell}{\partial z}, \text{flip}(W))$ 实际上还要将 $\frac{\partial \ell}{\partial z}$ padding至正确的维度。更具体地,需要向外扩 $K-1$ 个单位($K$ 是卷积核大小)。
stride
然后我们再分析更复杂的case,stride > 1 的情况。还是先看一个case
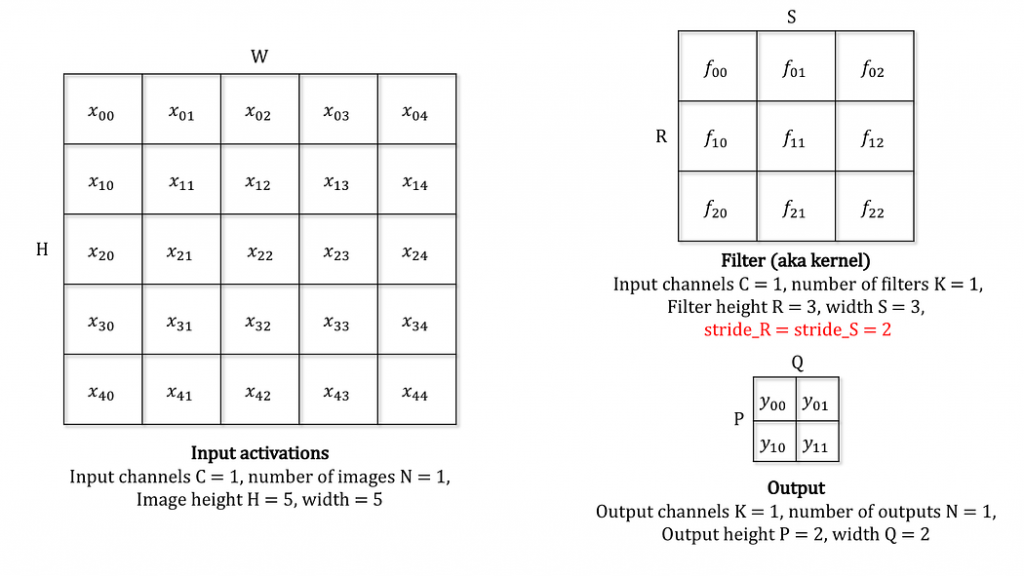
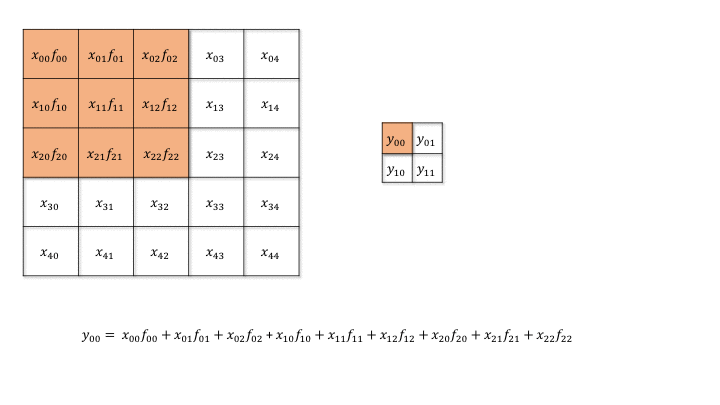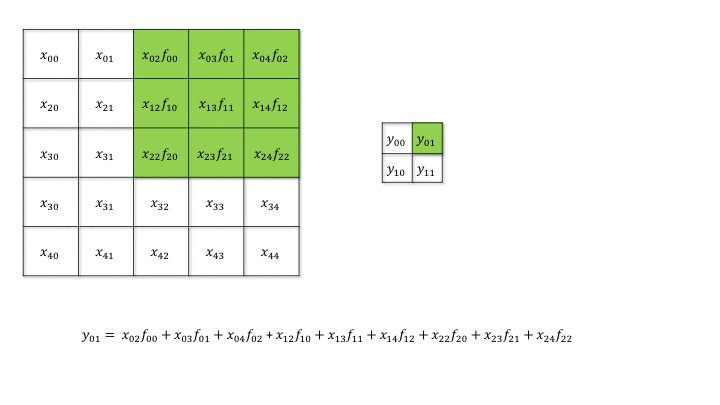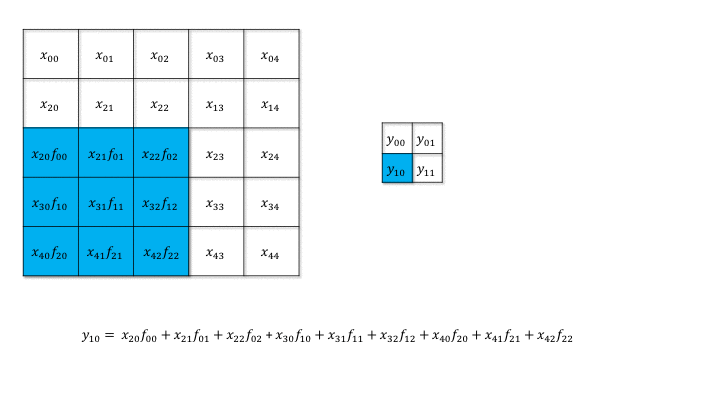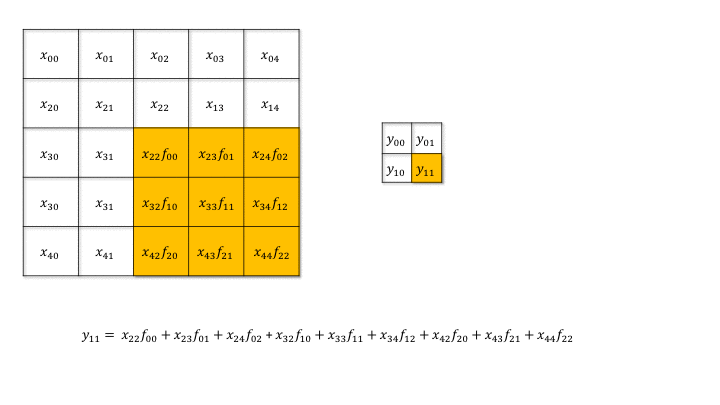
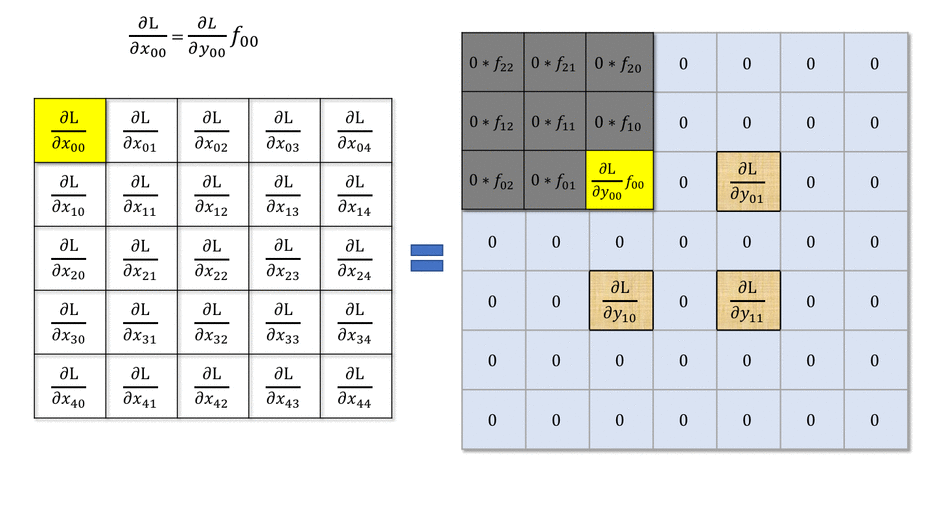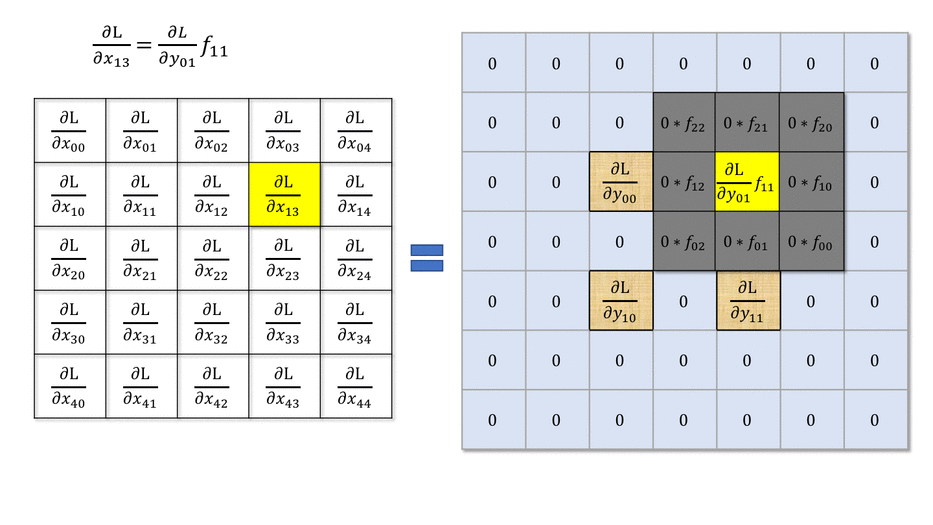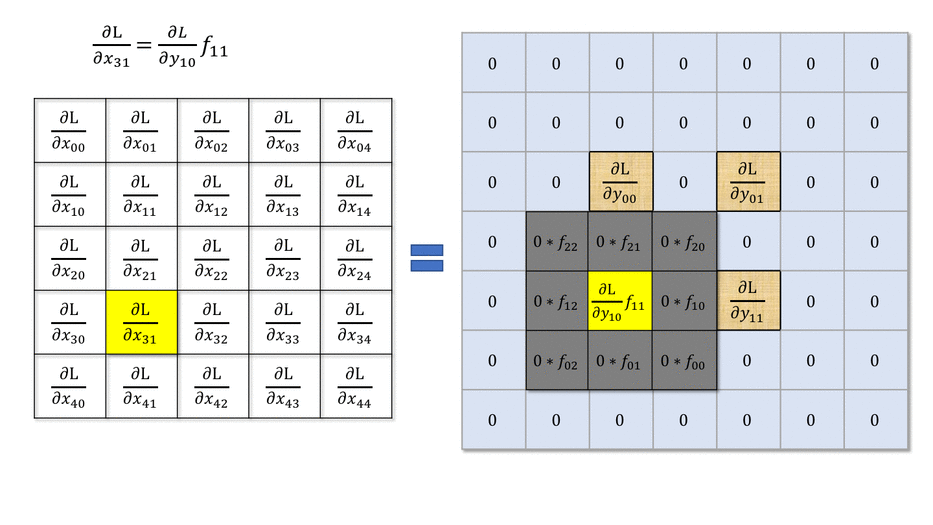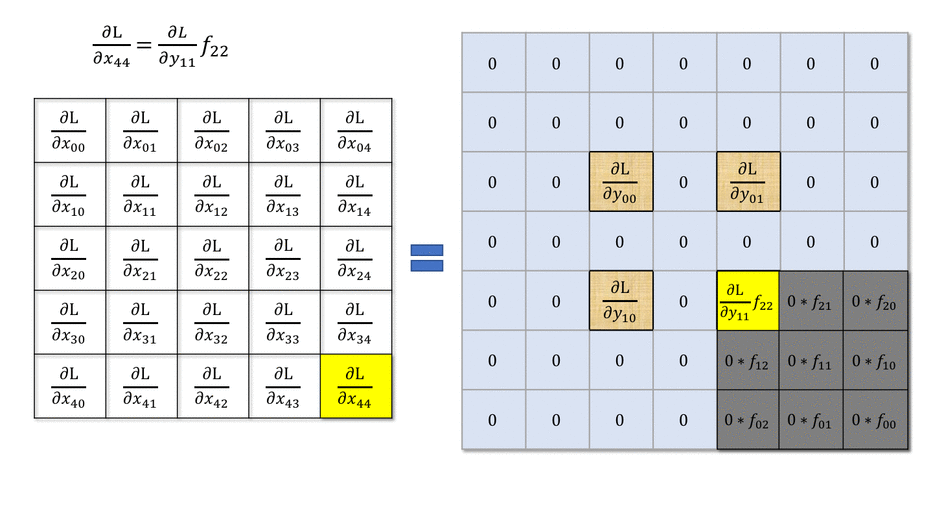
也就是说,我们前向传播中的stride表现在反向传播中就是dilate。
一个直观的理解是,一个 $H\times W$ 的图像,经过 $K\times K$ 的卷积核、步长为 $S$ 的二维卷积后,新图像的维度 $H^\prime\times W^\prime$ 将会是
$$
(\lfloor\frac{H-K}{s}\rfloor + 1) \times (\lfloor\frac{W-K}{s}\rfloor + 1)
$$
在反向传播中,我们需要将维度为 $H^\prime\times W^\prime$ 的 out_grad 变形到 $H\times W$,为了让图像大小的两个维度对齐,我们就需要dilate操作,也就是将 $H^\prime\times W^\prime$ 的维度恢复到了 $H^\prime s\times W^\prime s$。
在dilate操作之后,我们需要再padding $K-1$ 个单位,然后再进行 $\text{conv}(\frac{\partial \ell}{\partial z}, \text{flip}(W))$ 的二维卷积。此时就相当于是一个 $(H^\prime s+2(K-1))\times (W^\prime s+2(K-1))$ 的图像,经过 $K\times K$ 的卷积核、步长为 $1$ 的二维卷积,也就是说我们会得到一个
$$
(H^\prime s+(K-1))\times (W^\prime s+(K-1))
$$
的梯度 $\frac{\partial \ell}{\partial x}$。但是这显然是有一定问题的,因为我们期望的图像大小是 $H\times W$,而 $(H^\prime s+(K-1))\times (W^\prime s+(K-1))$ 不一定等于 $H\times W$,这里的问题实际上出在 dilate 操作上,$H^\prime = \lfloor\frac{H-K}{s}\rfloor + 1$,因为这里发生了向下取整,直接乘上 $s$ 就会导致图像放大的倍率可能有问题,因此在dilate操作时,我们需要将图像截断为
$$
[:H^\prime s-R_H,:W^\prime s-R_W]
$$
这里 $R_H=H^\prime s+(K-1)-H,R_W=W^\prime s+(K-1)-W$。这就能保证输出图像的维度对齐了。
general case
最后,我们再加入输入、输出和批次通道,也就是分析 $x\in\mathbb R^{N\times H\times W\times C_{in}}, W\in\mathbb R^{K\times K\times C_{in}\times C_{out}}$ 时的情况,由于 $z=\text{conv}(x,W)$ 的维度显然是 $N\times H^\prime\times W^\prime\times C_{out}$,所以回传梯度 out_grad 的梯度也是 $N\times H^\prime\times W^\prime\times C_{out}$。
这个梯度需要先进行dilate和pad处理、维度变成 $N\times (H^\prime s + 2(K-1)-R_H)\times (W^\prime s + 2(K-1)-R_W)\times C_{out}$,进行卷积的卷积核 $W$ 经过翻转后维度仍然是 $K\times K\times C_{in}\times C_{out}$,这里注意,反向传播需要将 out_grad 的维度变换到 x 的维度($C_{out}\to C_{in}$),因此还需要将 $W$ 的维度调整到 $K\times K\times C_{out}\times C_{in}$,然后调用之前写好的二维卷积前向传播函数即可。
$\frac{\partial \ell}{\partial W}$
stride
直接看上面的case,这次我们探究对于 $W$ 的梯度。
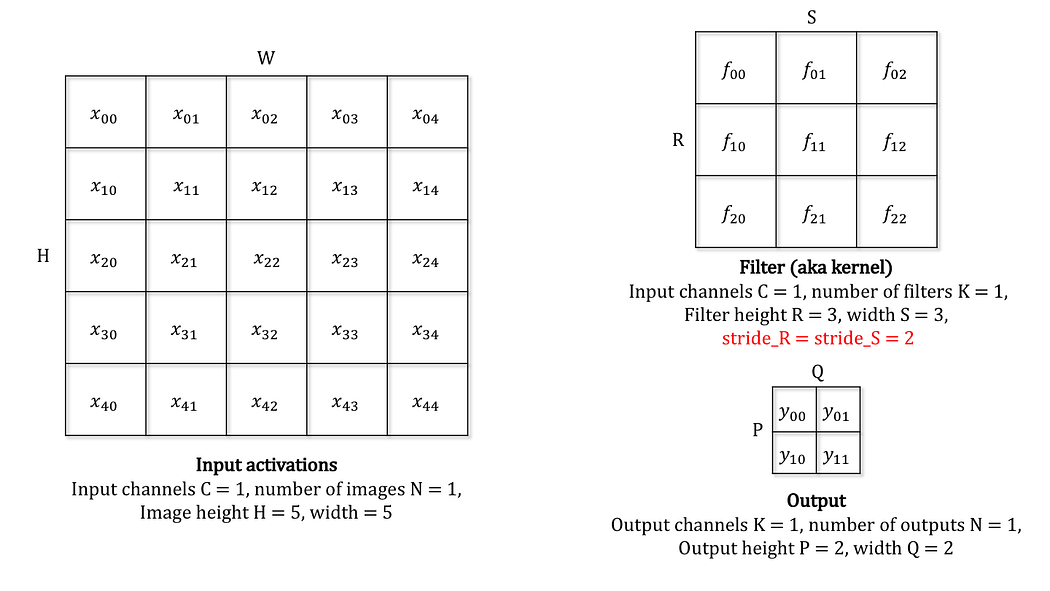
也就是图中的 \nabla_f。
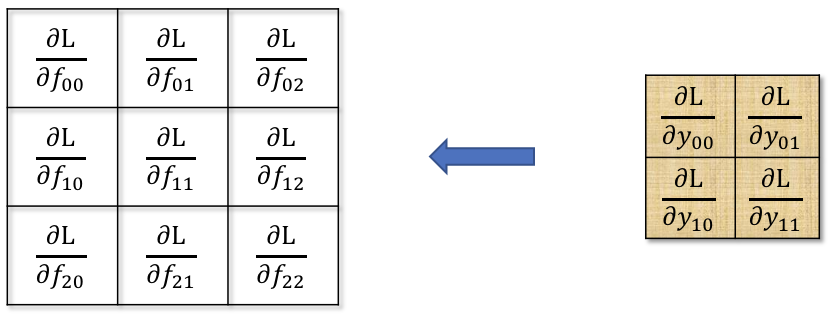
不同于 $\nabla_x$,$\nabla_f$ 中的元素在前向传播中是卷积核,进行了非常多的运算,且卷积核中的每一个元素都进行了相同次数($H^\prime\times W^\prime$ 次)的运算。
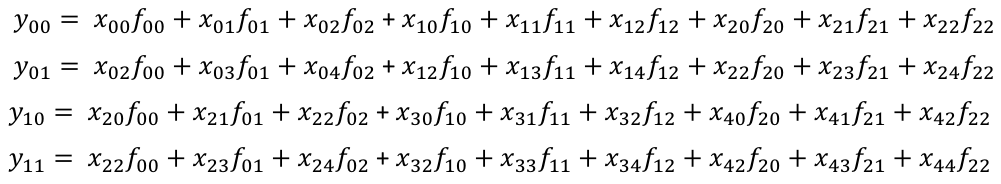
画图后不难发现
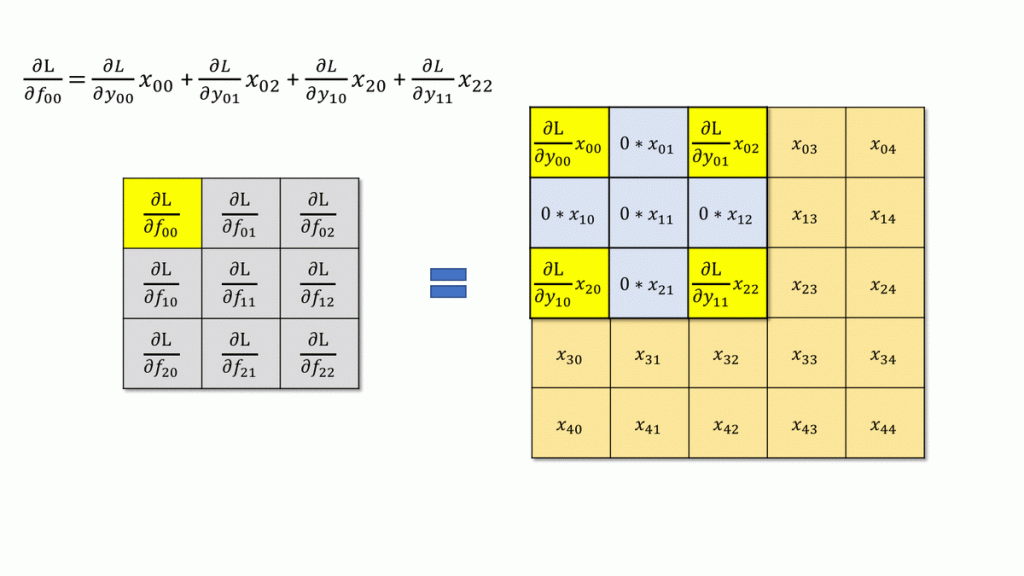
这实际上也是一个类似的卷积操作,这里我们需要将 out_grad 进行dilate操作,然后直接在 $x$ 上进行二维卷积。更具体地,这里的dilate等于 $stride-1$。回顾上文,求 $\nabla_x$ 时实际上我们也需要对 out_grad 进行相同的dilate操作。
general case
上面已经解决了单通道的case,现在我们再引入批次、输入输出通道,已知 $x\in\mathbb R^{N\times H\times W\times C_{in}}$,而dilate后的 $\text{out_grad}\in\mathbb R^{N\times (H^\prime s-R_H)\times (W^\prime s-R_W)\times C_{out}}$,这两个矩阵是不能直接卷积的,需要调整通道。根据步长为1的二维卷积的一般情况:$(N,H,W,C_{in})\times(K,K,C_{in},C_{out})\to (N,H-K+1,W-K+1,C_{out})$;由于这两个矩阵只有一个相同通道 $N$,因此 $N$ 在这里的起到 $C_{in}$ 的作用,此外,根据本文的假设 $H=W$,所以 $(H^\prime s-R_H)\times (W^\prime s-R_W)$ 起到卷积核 $(K\times K)$ 的作用,因此这里的维度需要变化为
$$
(C_{in}, H, W, N)\times (H^\prime s-R_H, W^\prime s-R_W, N, C_{out})\to (C_{in},H,W,C_{out})
$$
最后将维度调整为 $(H,W,C_{in},C_{out})$ 就是所求的 $\frac{\partial z}{\partial W}$ 了。
Code
def conv_with_grad_conference(x, W, out_grad, stride=1):
x_torch = torch.from_numpy(x)
x_torch = x_torch.permute(0, 3, 1, 2) # NCHW
x_torch.requires_grad = True
W_torch = torch.from_numpy(W)
W_torch = W_torch.permute(3, 2, 0, 1) # OIKK
W_torch.requires_grad = True
out_grad = torch.from_numpy(out_grad).permute(0, 3, 1, 2)
out = F.conv2d(x_torch, W_torch, stride=stride)
out.backward(out_grad)
return out.permute(0, 2, 3, 1).contiguous().detach().numpy(), x_torch.grad.detach().numpy(), W_torch.grad.detach().numpy()
# definitions
n = 3
cin = 2
cout = 4
h, w = 13, 13
k = 3
x = np.arange(n * h * w * cin, dtype=np.float64).reshape(n, h, w, cin)
W = np.arange(k * k * cin * cout, dtype=np.float64).reshape(k, k, cin, cout)
stride = 3
out_grad = np.random.randn(n, (h - k) // stride + 1, (w - k) // stride + 1, cout).astype(np.float64)
# conf
z, x_grad_torch, w_grad_torch = conv_with_grad_conference(x, W, out_grad, stride)
x_grad_torch = np.transpose(x_grad_torch, (0, 2, 3, 1)) # NCHW -> NHWC
w_grad_torch = np.transpose(w_grad_torch, (2, 3, 1, 0)) # OIKK -> KKIO
print('grad_x_torch', x_grad_torch.shape)
print('grad_W_torch', w_grad_torch.shape)
# nabla_x
out_grad = dilate(out_grad, (1, 2), stride - 1) # NH'W'O -> N(H's)(W's)O
rh = (h - k) // stride * stride + stride + k - 1 - h
rw = (w - k) // stride * stride + stride + k - 1 - w
out_grad = out_grad[:, :out_grad.shape[1] - rh, :out_grad.shape[2] - rw, :] # N(H's)(W's)O -> N(H's - rh)(W's - rw)O
out_grad2 = out_grad.copy()
out_grad = np.pad(out_grad, ((0, 0), (k - 1, k - 1), (k - 1, k - 1), (0, 0))) # N(H's - rh + 2(k - 1))(W's - rw + 2(k - 1))O
x_grad = conv_im2col(out_grad, np.transpose(np.flip(W, (0, 1)), (0, 1, 3, 2))) # NHWC
print('grad_x', x_grad.shape)
print(np.linalg.norm(x_grad - x_grad_torch))
# nabla_W
x = np.transpose(x, (3, 1, 2, 0)) # NHWC -> HWNC
out_grad2 = np.transpose(out_grad2, (1, 2, 0, 3)) # NH'W'O -> H'W'NO
print(x.shape, out_grad2.shape)
w_grad = conv_im2col(x, out_grad2) # IKKO
w_grad = w_grad.transpose((1, 2, 0, 3)) # KKIO
print('grad_w', w_grad.shape)
print(np.linalg.norm(w_grad - w_grad_torch))