本文是Lecture 6 – Fully connected networks, optimization, initialization、Lecture 7 – Neural Network Abstractions、Lecture 8 – Neural Network Library Implementation、Lecture 9 – Normalization and Regularization的笔记。以及dl sys hw2的部分实现。
Optimization
Gradient Descent
$$
\theta_{t+1}=\theta_t – \alpha\nabla_\theta \ell(\theta_t)
$$
这是梯度下降法的公式,其中 $\alpha$ 表示学习率。
Momentum
$$
\begin{aligned}
u_{t+1}&=\beta u_t + (1-\beta)\nabla_\theta\ell(\theta_t)\\
\theta_{t+1}&=\theta_t-\alpha u_{t+1}
\end{aligned}
$$
带动量的梯度下降法实际上就是多了一个被称为动量的参数,即上式中的 $u_{t+1}$,这个量是由之前的梯度累加得到,如果我们展开上方 $u_{t+1}$,就有
$$
u_{t+1} = (1-\beta)\nabla_\theta\ell(\theta_t) + \beta(1-\beta)\nabla_\theta\ell(\theta_{t-1}) + \beta^2(1-\beta)\nabla_\theta\ell(\theta_{t-2}) + \cdots
$$
这里,$\beta\in(0,1)$,也就是说动量 $u_{t+1}$ 会更根据时序对梯度进行加权。
一个比较简单的理解就是,动量是对之前所有梯度的加权,让梯度的变化更加平滑,减少梯度剧烈震荡的较劣情况。
Unbiasing
根据Momentum的公式可知,在算法的一开始,Momentum往往趋向于0,为了修正这种误差,可以使用去偏修正:
$$
\hat{u}_{t+1} = \frac{u_{t+1}}{1-\beta^t}
$$
也就是将 $u_{t+1}$ 放大,让动量在早期也不会太小。(多数情况下可能增加收敛速度)
Adam
$$
\begin{aligned}
u_{t+1}&=\beta_1 u_t + (1-\beta_1)\nabla_\theta\ell(\theta_t)\\
v_{t+1}&=\beta_2 v_t + (1-\beta_2)(\nabla_\theta\ell(\theta_t))^2\quad\text{(element-wise)}\\
\theta_{t+1}&=\theta_t-\frac{\alpha u_{t+1}}{\sqrt{v_{t+1}}+\epsilon}\quad\text{(element-wise)}
\end{aligned}
$$
Adam加入了一个二阶矩估计 $v_{t+1}$。
Unbiasing
同理,Adam往往也会引入去偏修正:
$$
\begin{aligned}
\hat{u}_{t+1} &= \frac{u_{t+1}}{1-\beta_1^t}\
\hat{v}_{t+1} &= \frac{v_{t+1}}{1-\beta_2^t}\
\end{aligned}
$$

$\ell_2$ Regularization a.k.a. weight decay
考虑经典机器学习的优化问题
$$
\min_{\theta} \frac {1}{m}\sum_{i=1}^m \ell(h_\theta(x^{(i)}),y^{(i)})
$$
如果模型的参数都较小,那么直觉上模型每一次优化的变化幅度也会较小,也就是说模型的输出比较平滑、稳定。此时我们可以认为模型已经比较优秀。
注意这个直觉对于深度学习可能并不怎么成立(比如全0的FCN会输出0),这只是一种可能的理解方法。
因此,我们经常给优化目标加上一个正则项:
$$
\min_{\theta} \frac {1}{m}\sum_{i=1}^m \ell(h_\theta(x^{(i)}),y^{(i)}) + \frac\lambda 2 \sum_{j=1}^L ||W_i||^2_{\text F}
$$
也就是神经网络中每一层中参数的平方和开根。这里在数学上用Frobenius范数表达,也就是作用于矩阵的 $\ell_2$ 范数。
对于优化器的更新就变成了
$$
W_i \leftarrow W_i – \alpha\nabla_{W_i} \ell(W_i) – \alpha\lambda W_i
$$
注意到上式可以简写为
$$
W_i \leftarrow (1-\alpha\lambda)W_i – \alpha\nabla_{W_i} \ell(W_i)
$$
这里 $(1-\alpha\lambda)$ 可以认为是对于原矩阵 $W_i$ 权重的一次缩小,因此在dl sys中被称为weight decay。
Implementation
class SGD(Optimizer):
def __init__(self, params, lr=0.01, momentum=0.0, weight_decay=0.0):
super().__init__(params)
self.lr = lr
self.momentum = momentum
self.u = {}
self.weight_decay = weight_decay
def step(self):
### BEGIN YOUR SOLUTION
for i, p in enumerate(self.params):
if i not in self.u:
self.u[i] = 0
new_grad = p.grad + self.weight_decay * p.data
new_grad = ndl.Tensor(new_grad, dtype='float32')
self.u[i] = self.momentum * self.u[i] + (1 - self.momentum) * new_grad
p.data -= self.u[i] * self.lr
class Adam(Optimizer):
def __init__(
self,
params,
lr=0.01,
beta1=0.9,
beta2=0.999,
eps=1e-8,
weight_decay=0.0,
):
super().__init__(params)
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.weight_decay = weight_decay
self.t = 0
self.m = {}
self.v = {}
def step(self):
### BEGIN YOUR SOLUTION
self.t += 1
for i, p in enumerate(self.params):
if i not in self.m:
self.m[i] = 0
self.v[i] = 0
if p.grad is None:
continue
new_grad = (p.grad.detach() + self.weight_decay * p.detach()).detach()
new_grad = ndl.Tensor(new_grad, dtype='float32')
self.m[i] = (self.beta1 * self.m[i]) + ((1 - self.beta1) * new_grad)
self.v[i] = (self.beta2 * self.v[i]) + ((1 - self.beta2) * (new_grad ** 2))
unbiased_m = self.m[i] / (1 - self.beta1 ** self.t)
unbiased_v = self.v[i] / (1 - self.beta2 ** self.t)
p.data -= (self.lr * unbiased_m / (unbiased_v ** 0.5 + self.eps)).detach()
### END YOUR SOLUTIONInitialization
0-initialization
不同于凸优化,在深度学习中,不建议将模型的参数全部赋值为0。这是因为凸优化中问题结构是凸的,而深度学习一般都是非凸的。
在FCN中,如果模型参数一开始全为0,那么就有
$$
Z_{i+1} = \sigma_i(Z_iW_i)=0
$$
也就是模型输出是全0,没有任何有效信息。
此外,
$$
\frac{\partial \ell(Z_{L+1},y)}{\partial W_i} = \nabla_{W_i}\ell(Z_{L+1},y) = Z_i^T \cdot (G_{i+1}\circ \sigma^\prime(Z_iW_i)) = 0
$$
也就是说梯度也是全0,这意味着我们在一个鞍点上,这不利于模型的收敛。
Initialization vs Optimization
首先很容易想到我们可以随机设置参数,比如正态分布、均匀分布……
但是怎么衡量参数设置是否合理?一个比较简单的量化标准就是:每一层神经网络的参数都应该尽量符合相同的分布。
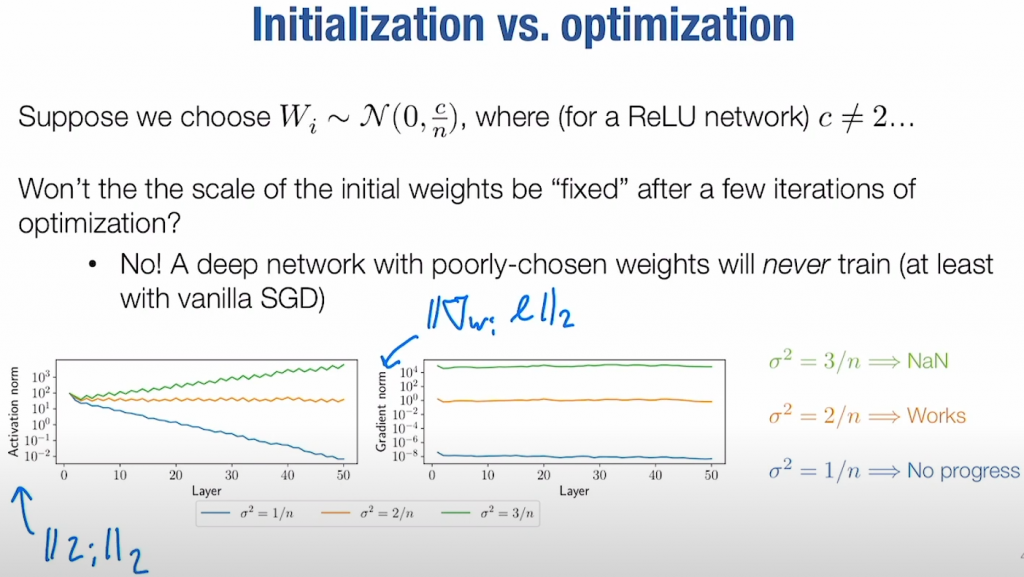
上图展示了假设第 $i$ 层的参数设置为 $W_i\sim \mathcal{N}(0, \frac c n)$ 时,每一层神经网络参数的分布变化情况。只有 $W_i\sim \mathcal{N}(0,\frac 2n)$ 时,神经网络的参数分布才维持稳定(这里 $n$ 表示神经元数量、or参数量)。
Kaiming Initialization
上一小节提到的初始化方法就是Kaiming Initialization,具体有两种变体Kaiming uniform和Kaiming normal。
Kaiming uniform
$$
\mathcal U (-\text{bound}, \text{bound}),\ \text{bound} = \text{gain}\times \sqrt{\frac {3}{\text{fan_in}}}
$$
Kaiming normal
$$
\mathcal N(0, \text{std}^2),\ \text{std} =\text{gain} \sqrt{\frac{1}{\text{fan_in}}}
$$
对于激活函数 ReLU 而言,推荐将 $\text{gain}$ 设置为 $\sqrt 2$。
Implementation
def xavier_uniform(fan_in, fan_out, gain=1.0, **kwargs):
### BEGIN YOUR SOLUTION
a = gain * math.sqrt(6 / (fan_in + fan_out))
return rand(fan_in, fan_out, low=-a, high=a, **kwargs)
### END YOUR SOLUTION
def xavier_normal(fan_in, fan_out, gain=1.0, **kwargs):
### BEGIN YOUR SOLUTION
s = gain * math.sqrt(2 / (fan_in + fan_out))
return randn(fan_in, fan_out, std=s, **kwargs)
### END YOUR SOLUTION
def kaiming_uniform(fan_in, fan_out, nonlinearity="relu", **kwargs):
assert nonlinearity == "relu", "Only relu supported currently"
### BEGIN YOUR SOLUTION
b = math.sqrt(2) * math.sqrt(3 / (fan_in))
return rand(fan_in, fan_out, low=-b, high=b, **kwargs)
### END YOUR SOLUTION
def kaiming_normal(fan_in, fan_out, nonlinearity="relu", **kwargs):
assert nonlinearity == "relu", "Only relu supported currently"
### BEGIN YOUR SOLUTION
s = math.sqrt(2 / fan_in)
return randn(fan_in, fan_out, std=s, **kwargs)
### END YOUR SOLUTIONNormalization
虽然Kaiming Initialization对于ReLU有较好的表现,但是在更复杂神经网络的训练过程中,很难仅通过初始化保证网络的稳定性。
一个更好的思路是,在训练过程中对每一层都加上一个normal运算,让参数保证分布稳定。
Layer norm
最常见的normalization就是Z-Score Normalization,也就是
$$
Z=\frac{X-\mu}{\sigma}
$$
这么做可以令随机数据的期望为 $0$,方差为 $1$。而layer norm的思路也正是如此,
$$
y = w \circ \frac{x_i – \textbf{E}[x]}{((\textbf{Var}[x]+\epsilon)^{1/2})} + b
$$
这里 $\textbf{E}[x]$ 表示输入的期望,$\textbf{Var}[x]$ 表示输入的方差,$\epsilon$ 是一个极小的数(用于防止除0),$w,b$ 是layer norm layer的可训练参数。
layer norm的核心思想是对于每一个输入数据进行标准化,以二维数据为例,假设 $A$ 是一个大小为 $(B,N)$ 的矩阵,其中第一维是 batc_size,第二维是输入数据的长度,那么就有
$$
\begin{aligned}
\textbf{E}[x_i] &= \frac{1}{n}\sum_{j=1}^n x_{i,j}\\
\textbf{Var}[x_i] &= \frac{1}{n}\sum_{j=1}^n (x_{i,j} – \textbf{E}[x_i])^2
\end{aligned}
$$
也就是对于一个二维矩阵(第一维是batch),layer norm就是对每一行(每一例数据)进行标准化。
Implementation
class LayerNorm1d(Module):
def __init__(self, dim, eps=1e-5, device=None, dtype="float32"):
super().__init__()
self.dim = dim
self.eps = eps
### BEGIN YOUR SOLUTION
self.weight = Parameter(init.ones(1, dim, requires_grad=True))
self.bias = Parameter(init.zeros(1, dim, requires_grad=True))
### END YOUR SOLUTION
def forward(self, x: Tensor) -> Tensor:
### BEGIN YOUR SOLUTION
mean = ops.summation(x, (1,)) / x.shape[1]
mean = ops.reshape(mean, (mean.shape[0], 1))
mean = ops.broadcast_to(mean, x.shape)
var = ops.power_scalar(x - mean, 2) + self.eps
var = ops.summation(var, (1,)) / x.shape[1]
var = ops.reshape(var, (var.shape[0], 1))
std = ops.power_scalar(var, 0.5)
std = ops.broadcast_to(std, x.shape)
y = (x - mean) / std
ln_x = ops.broadcast_to(self.weight, x.shape) * y + ops.broadcast_to(self.bias, x.shape)
return ln_x
### END YOUR SOLUTIONBatch norm
batch norm的思想和layer norm是一样的,不同点在于它是沿batch维度进行的标准化,如下图。

Minibatch dependency
batch norm实际上存在一个问题:它沿着batch维度进行标准化,但是在实际场景中我们喂给模型的是minibatch(也就是每次训练都是部分数据),因此模型的标准化只能考虑局部的minibatch。一个常见的解决方案是用类似动量的方法更新均值和方差,并在推理阶段采用这个经验均值&方差。
$$
\hat{\mu}_{i+1} = \beta\hat{\mu}_{i} + (1-\beta)\textbf{E}(x_{i+1})
$$
训练过程中仍然直接用当前batch的均值和方差进行标准化。
Implementation
class BatchNorm1d(Module):
def __init__(self, dim, eps=1e-5, momentum=0.1, device=None, dtype="float32"):
super().__init__()
self.dim = dim
self.eps = eps
self.momentum = momentum
### BEGIN YOUR SOLUTION
self.weight = Parameter(init.ones(1, dim, requires_grad=True))
self.bias = Parameter(init.zeros(1, dim, requires_grad=True))
self.running_mean = init.zeros(dim) # 不是parameter 不要加parameter!
self.running_var = init.ones(dim)
### END YOUR SOLUTION
def forward(self, x: Tensor) -> Tensor:
### BEGIN YOUR SOLUTION
if self.training:
mean = ops.summation(x, (0,)) / x.shape[0]
# self.running_xxx 需要加detach() 不然无法通过test_optim_adam_z_memory_check_1()
self.running_mean = self.momentum * mean.detach() + (1 - self.momentum) * self.running_mean.detach()
mean = ops.broadcast_to(mean, x.shape)
var = ops.summation((x - mean) ** 2, (0,)) / x.shape[0]
self.running_var = self.momentum * var.detach() + (1 - self.momentum) * self.running_var.detach()
std = ops.power_scalar(var + self.eps, 0.5)
std = ops.broadcast_to(std, x.shape)
y = (x - mean) / std
bn_x = ops.broadcast_to(self.weight, x.shape) * y + ops.broadcast_to(self.bias, x.shape)
return bn_x
else:
mean = ops.broadcast_to(self.running_mean, x.shape)
std = ops.power_scalar(ops.broadcast_to(self.running_var + self.eps, x.shape), 0.5)
y = (x - mean) / std
bn_x = ops.broadcast_to(self.weight, x.shape) * y + ops.broadcast_to(self.bias, x.shape)
return bn_x
### END YOUR SOLUTIONhw2
这一节主要聚焦于上文中未提到的、但在hw2中较为重要的部分。
$\text{LogSumExp}$
首先,$\text{LogSumExp}$ 的公式如下($z$ 表示一个向量 $(z_1,z_2,\ldots,z_n)$)
$$
\text{LogSumExp}(z) = \log\bigg( \sum_i \exp(z_i) \bigg)
$$
也就是对 $\exp(x_i)$ 求和再套 $\log$,该式子可以和DL中另一个常见的式子 $\text{softmax}(z) = \frac{\exp(z)}{\sum_i \exp(z_i)}$ 相互转换:
$$
\begin{aligned}
\text{softmax}(z) &= \frac{\exp(z)}{\sum_i \exp(z_i)}\\
&= \exp(\log(\frac{\exp(z)}{\sum_i \exp(z_i)}))\\
&= \exp(\log(\exp(z)) – \log(\sum_i \exp(z_i)))\\
&= \exp(z – \text{LogSumExp}(z))
\end{aligned}
$$
不过在实际计算中,为了数值稳定性,我们常常对这个定义式进行微调:
$$
\text{LogSumExp}(z) = \log\bigg( \sum_i \exp(z_i-c) \bigg) + c
$$
这里 $c$ 是一个标量,这可以使得 $\exp(z_i)$ 不会过大导致严重影响浮点数运算的精度,而 $c$ 往往取值为 $\max(z)$,这就保证了 $z_i-c\le 0$。
$$
\begin{aligned}
\nabla_{z_i} \text{LogSumExp}(z) &= \frac{\partial }{\partial z_i}\log (\sum_{j} \exp (z_j – \max{z})) + \frac{\partial }{\partial z_i}\max{z}\\
&= \frac{1}{\sum_{j}\exp(z_j – \max z)}\frac{\partial \sum_{j}\exp(z_j – \max z)}{\partial z_i}\\
&= \frac{\exp(z_i-\max z)}{\sum_{j}\exp(z_j – \max z)}\\
&= \text{softmax}(z_i)
\end{aligned}
$$
注意这里 $\max z$ 被视作一个标量,不参与求导。综上可知
$$
\nabla_{z} \text{LogSumExp}(z) = \text{softmax}(z)
$$
由于在前向推理中已经求出了 $\text{LogSumExp}(z)$,所以求梯度只需要计算
$$
\text{softmax}(z) = \exp(z-\text{LogSumExp}(z)) \quad(\text{LogSumExp}(z)\text{ has been computed.})
$$
class LogSumExp(TensorOp):
def __init__(self, axes: Optional[tuple] = None):
self.axes = axes
def compute(self, Z):
### BEGIN YOUR SOLUTION
max_z = array_api.max(Z, self.axes, keepdims=True)
exp_z = array_api.exp(Z - max_z)
lse = array_api.log(array_api.sum(exp_z, axis=self.axes)) + array_api.max(Z, axis=self.axes)
return lse
### END YOUR SOLUTION
def gradient(self, out_grad, node):
### BEGIN YOUR SOLUTION
Z = node.inputs[0]
lse_z = node
# lse_z = logsumexp(Z, self.axes) # also correct
if self.axes:
new_shape = [1] * len(Z.shape)
for i in range(len(Z.shape)):
if i not in self.axes:
new_shape[i] = Z.shape[i]
out_grad = reshape(out_grad, new_shape)
lse_z = reshape(lse_z, new_shape)
return out_grad * exp(Z - lse_z)
### END YOUR SOLUTION需要注意的是这里的 sum 操作会压缩掉某些维度(self.axes),在计算梯度之前要将这些维度恢复。
$\text{LogSoftmax}$ and Jacobian Vector Product
$\text{LogSoftmax}$ 就是先softmax,再套一个log,即
$$
\text{LogSoftmax}(z) = \log\bigg( \text{softmax(z)} \bigg) = z – \text{LogSumExp}(z)
$$
需要额外注意的是这里的特殊定义:
Applies a numerically stable logsoftmax function to the input by subtracting off the maximum elements. Assume the input NDArray is 2 dimensional and we are doing softmax over
axis=1.
也就是说这个函数的输入保证是一个二维数组,且固定对维度1进行softmax,因此实现上和logsumexp有轻微的不同。
$$
\begin{aligned}
\nabla_{z_i} \text{LogSoftmax}(z) &= \frac{\partial }{\partial z_i}z – \frac{\partial }{\partial z_i} \text{LogSumExp}(z)\\
&= \delta_{i,j} -\text{softmax}(z)\quad(\delta_{i=j}=1,\delta_{i\neq j}=0)
\end{aligned}
$$然后我发现我返回的 $\nabla_{z}*\text{out_grad}$ 在数值上出问题了。
实际上,计算图维护的是结点的雅可比向量积,也就是
$$
\mathbf{J} = \begin{bmatrix}
\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}
\end{bmatrix}
$$
$$
\mathbf{JVP} = \mathbf{J} \cdot \mathbf{v} = \begin{bmatrix}
\sum_{i=1}^n \frac{\partial y_1}{\partial x_i} v_i \\
\sum_{i=1}^n \frac{\partial y_2}{\partial x_i} v_i \\
\vdots \\
\sum_{i=1}^n \frac{\partial y_m}{\partial x_i} v_i
\end{bmatrix}
$$
但是需要注意的是,这里我们本质上还是在对向量进行分析,但是模型中需要计算的是矩阵。
具体到一个case,假设 node 为 $\pmatrix{-1.64 & -2.79 & -0.29\\ -0.68 & -1.33 & -1.48\\ -0.16 & -3.06 & -2.26}$,out_grad 为 $\pmatrix{-3.29 & -5.59 &-0.59\\ -1.36 & -2.66 & -2.96\\ -0.33 & -6.13 & -4.52}$。
这里的 node 实际上有3个jacobian,我们要对每一行分别计算 $\textbf J$,这里以第一行为例。首先给出第一行的softmax normalize:$\pmatrix{0.19 & 0.06 & 0.75}$。
$$
\textbf J = \begin{bmatrix}
1 – \text{softmax}(x_{1,1}) & -\text{softmax}(x_{1,1}) & -\text{softmax}(x_{1,1})\\
-\text{softmax}(x_{1,2}) & 1 – \text{softmax}(x_{1,2}) & -\text{softmax}(x_{1,2})\\
-\text{softmax}(x_{1,3}) & -\text{softmax}(x_{1,3}) & 1 – \text{softmax}(x_{1,3})
\end{bmatrix} = \begin{bmatrix}
0.81 & -0.19 & -0.19\\
-0.06 & 0.94 & -0.06\\
-0.75 & -0.75 & 0.25
\end{bmatrix}
$$
然后要注意,这个jacobian是第一行的jacobian,因此只作用于 out_grad 的第一行,也就是
$$
\mathbf{JVP} = \mathbf{J} \cdot \mathbf{v}=\begin{bmatrix}
0.81 & -0.19 & -0.19\\
-0.06 & 0.94 & -0.06\\
-0.75 & -0.75 & 0.25
\end{bmatrix}
\begin{bmatrix}
-3.29\\
-5.59\\
-0.59
\end{bmatrix}
=\begin{bmatrix}
-1.49\\
-5.02\\
6.51
\end{bmatrix}
$$
最后将维度调整回去:$\pmatrix{-1.49 & -5.02 & 6.51}$。对于3行分别进行相同处理,最后堆叠到一起即可。
因此,一定要理清楚jacobian和输入梯度之间的对应关系。
class LogSoftmax(TensorOp):
def compute(self, Z):
### BEGIN YOUR SOLUTION
max_Z = array_api.max(Z, 1, keepdims=True)
exp_Z = array_api.exp(Z - max_Z)
lse_Z = array_api.log(array_api.sum(exp_Z, 1, keepdims=True)) + array_api.max(Z, 1, keepdims=True)
return Z - lse_Z
### END YOUR SOLUTION
def gradient(self, out_grad, node):
### BEGIN YOUR SOLUTION
softmax_Z = exp(node)
out_sum = summation(out_grad, 1).realize_cached_data()
grad_Z = softmax_Z.realize_cached_data()
for i in range(grad_Z.shape[0]):
grad_Z[i, :] *= out_sum[i]
res = out_grad - Tensor(grad_Z)
return res
### END YOUR SOLUTIONDataloader
Dataloader的作用很简单,就是将dataset的数组打包,转变为minibatch的形式,具体而言要实现两个函数 __iter__ 和 __next__,这里 __iter__ 实现的是开启一轮新的迭代,__next__ 则是取出当前的minibatch。
class DataLoader:
r"""
Data loader. Combines a dataset and a sampler, and provides an iterable over
the given dataset.
Args:
dataset (Dataset): dataset from which to load the data.
batch_size (int, optional): how many samples per batch to load
(default: ``1``).
shuffle (bool, optional): set to ``True`` to have the data reshuffled
at every epoch (default: ``False``).
"""
dataset: Dataset
batch_size: Optional[int]
def __init__(
self,
dataset: Dataset,
batch_size: Optional[int] = 1,
shuffle: bool = False,
):
self.dataset = dataset
self.shuffle = shuffle
self.batch_size = batch_size
if not self.shuffle:
self.ordering = np.array_split(np.arange(len(dataset)),
range(batch_size, len(dataset), batch_size))
def __iter__(self):
### BEGIN YOUR SOLUTION
if self.shuffle:
order = np.arange(len(self.dataset))
np.random.shuffle(order)
self.ordering = np.array_split(order, range(self.batch_size, len(self.dataset), self.batch_size))
self.current_index = 0
### END YOUR SOLUTION
return self
def __next__(self):
### BEGIN YOUR SOLUTION
if self.current_index >= len(self.ordering):
raise StopIteration
batches = [Tensor(x) for x in self.dataset[self.ordering[self.current_index]]]
self.current_index += 1
return batches
### END YOUR SOLUTION