这是Deep Learning Systems Lecture 2 – ML Refresher / Softmax Regression的学习笔记。
Three Ingredients of ML algorithm
- The hypothesis class也就是将输入映射到输出的程序流程。
- Loss function用于衡量hypothesis class表现如何。
- An optimized method减小loss、优化参数的方法。
The Softmax Regression Optimization Problem
Notation
- 假设问题的输入是一个长为 $n$ 的一维向量,所求输出是一个长为 $k$ 的一维向量,输入数据一共有 $m$ 个。比如,MNIST训练集有 $60000$ 幅图像,每幅图像都是 $28\times 28$ 的灰度图,需要分为 $10$ 种数字类别。对应本节描述就是 $n=28\times 28=784,k=10,m=60000$。
- hypothesis class $h:\mathbb R^n \to \mathbb R^k$,也就是将输入映射到输出的函数。特别地,在本文中将采用线性算子作为hypothesis class,也就是
$$
h_{\theta}(x) = \theta^T x
$$
这里 $\theta\in\mathbb R^{n\times k}$。(也就是一个简单的线性加权,因为 $x\in \mathbb R^{n\times 1}$) - Matrix batch notation在实际情况下,我们往往会将数据打包为矩阵,而不是单独处理一维向量,因此有以下matrix batch notation:
$$
X\in\mathbb{R}^{m\times n} = \pmatrix{ x^{(1)^{T}}\\ \vdots\\ x^{(m)^{T}}\\ }
$$
$$
y\in\{1,\ldots,k\}^m = \pmatrix{ y^{(1)}\\ \vdots\\ y^{(m)} }
$$
这里 X 表示将输入打包后的矩阵,y 表示对应的标签(not one-hot)。将线性假设应用到batch中,就有
$$
h_{\theta}(X) = \pmatrix{ h_{\theta}(x^{(1)^T})\\ \vdots\\ h_{\theta}(x^{(m)^T})\\ }
$$
Softmax / Cross-Entropy Loss
softmax的作用往往是将hypothesis class的输出转为概率,
$$
z_i = P(label=i) = \frac{\exp(h_i(x))}{\sum_{j=1}^k\exp(h_j(x))}\Leftrightarrow z = \text{normalize}(\exp(h(x)))
$$
这里 $z\in\mathbb{R}^{k}$,表示将输出 $h(x)$ 通过softmax转换为概率分布。
Cross-Entropy Loss是最常见的loss function,表示为
$$
\begin{aligned} \ell_{ce}(h(x),y) &= -\log P(label=y)\\ &= -\log \frac{\exp(h_y(x))}{\sum_{j=1}^k\exp(h_j(x))}\\ &= -\log \exp(h_y(x)) + \log \sum_{j=1}^k \exp(h_j(x))\\ &= -h_y(x) + \log \sum_{j=1}^k \exp(h_j(x)) \end{aligned}
$$
The Softmax Regression Optimization Problem
我们可以将机器学习的三个组成成分简化为一个优化问题:
$$
\min_{\theta} \frac {1}{m}\sum_{i=1}^m \ell(h_\theta(x^{(i)}),y^{(i)})
$$
即最小化hypothesis class的平均loss。
在本文中则是
$$
\min_{\theta} \frac {1}{m}\sum_{i=1}^m \ell_{ce}(\theta^Tx^{(i)},y^{(i)})
$$
Gradient Descent
Gradient Descent
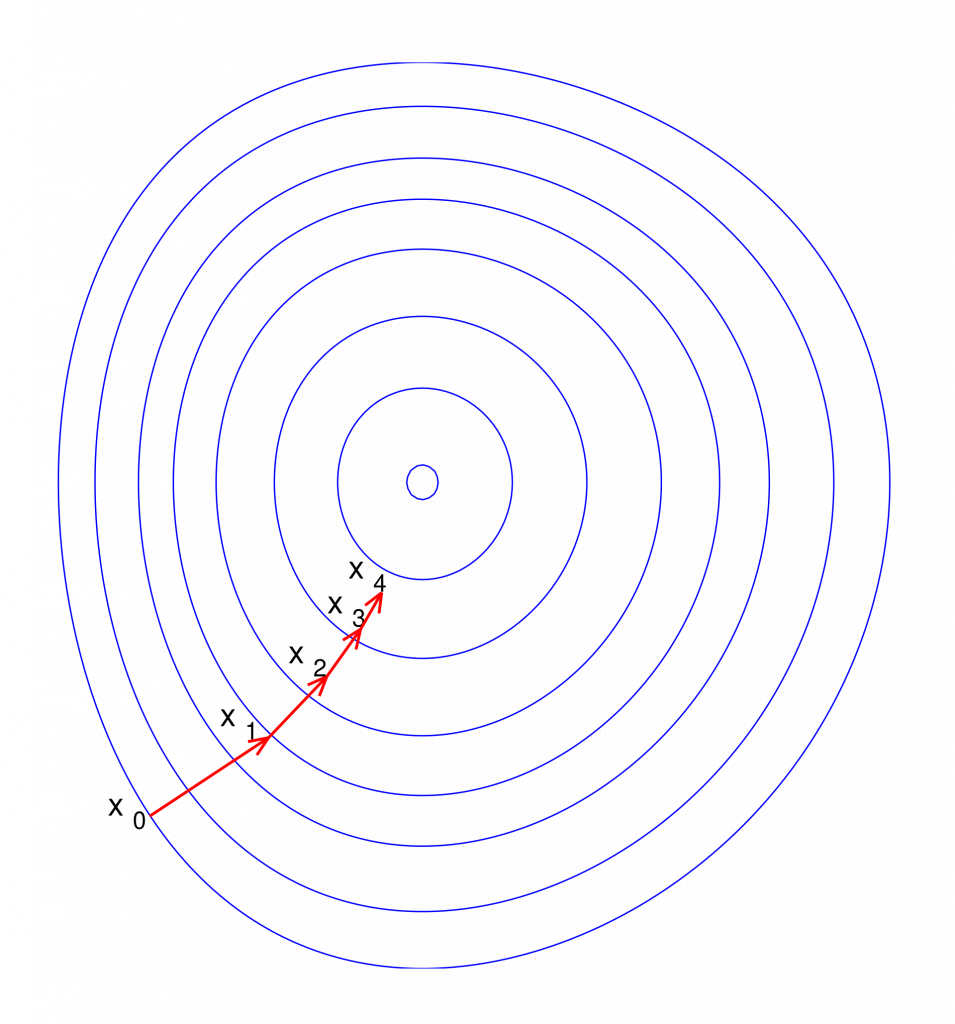
Stochastic Gradient Descent
相较于直接的梯度下降,机器/深度学习中往往采用Stochastic Gradient Descent,即随机梯度下降。这里,Stochastic体现在计算梯度时,并不是使用整个训练集来计算,而是随机选取训练集中的一个小批量样本来估算梯度,从而进行参数更新。
具体地,传统的梯度下降方法(Batch Gradient Descent)会在每次迭代中使用整个训练集来计算梯度并更新模型参数,这会导致计算成本非常高,尤其是在训练集很大的时候。而在SGD中,每次参数更新是基于单个样本或者小批量样本的梯度。
这种随机选择的方式带来了两个主要特点:
- 计算速度更快:由于每次迭代只计算一个小批量或单个样本的梯度,计算时间比全量梯度下降要短。
- 噪声性:由于每次梯度计算只基于部分样本,所以梯度更新会带有噪声,表现为更不稳定的更新路径。这种噪声在短期内可能导致不收敛或震荡,但长远来看,可以帮助跳出局部最优解,从而找到更好的全局最优解。
具体可以表示为:
Repeat:
- Sample a minibatch of data $X\in \mathbb R^{B\times n}, y\in{1,\ldots,k}^B$
- Update parameters $\theta:= \theta – \frac{\alpha}{B}\sum_{i=1}^B\nabla_\theta\ell(h_{\theta}(x^{(i)},y^{(i)}))$
The Gradient of the Softmax Objective
$\nabla_{\theta}\ell_{ce}(\theta^T x,y)$
目标:计算 $\nabla_{\theta}\ell_{ce}(\theta^T x,y)$。
首先我们计算交叉熵的偏导数,也就是 $\frac{\partial \ell_{ce}(h,y)}{\partial h_i}$,
$$
\begin{aligned}
\frac{\partial \ell_{ce}(h,y)}{\partial h_i} &= \frac{\partial }{\partial h_i}(-h_y+\log \sum_{j=1}^k \exp(h_j))\\
&= -[i=y] + \frac{\frac{\partial }{\partial h_i}\sum_{j=1}^k \exp(h_j)}{\sum_{j=1}^k \exp(h_j)}\\
&= -[i=y] + \frac{\exp(h_i)}{\sum_{j=1}^k \exp(h_j)}
\end{aligned}
$$
不难发现该式的后半部分就是softmax,所以 $\nabla_h \ell_{ce}(h,y)$ 可以表示为
$$
\nabla_h \ell_{ce}(h,y) = z – e_y
$$
$z = \text{normalize}(\exp(h))$,$e_y$ 则是标签 $y$ 的one-hot编码。
然后我们再计算 $\nabla_{\theta}\ell_{ce}(\theta^T x,y)$,注意这里对矩阵的求导我们假设“一切都是标量”,然后直接对 $\theta$ 应用链式法则,并且按经验重排矩阵的维度,而不是正常的严谨数学推导(多元微积分)。
$$
\begin{aligned}
\frac{\partial}{\partial \theta} \ell_{ce}(\theta^T x,y) &= \frac{\partial \ell_{ce}(\theta^T x,y)}{\partial \theta^T x} \cdot \frac{\partial \theta^T x}{\partial \theta}\\
&= (z-e_y)\cdot x
\end{aligned}
$$
注意这个链式法则的左半部就是上方推导的交叉熵的偏导数,而后半部分就是对线性加权的偏导。
但是这有个问题,$z-e_y$ 和 $x$ 的维度不能直接点乘,根据维度 $z-e_y\in\mathbb R^{k\times 1}, x\in\mathbb R^{n\times 1}$,然后,不难分析出 $\frac{\partial}{\partial \theta} \ell_{ce}(\theta^T x,y)$ 的维度应该和 $\theta$ 是一样的($\theta$ 需要直接减去这个gradient),所以我们应该将维度改写成 $x\cdot(z-e_y)^T$,即
$$
\begin{aligned}
\frac{\partial}{\partial \theta} \ell_{ce}(\theta^T x,y) &= x\cdot(z-e_y)^T
\end{aligned}
$$
实际上就是完全按照经验调整维度。
matrix batch
实际上,我们一般是对输入打包进行处理,也就是所谓的matrix batch,这种暴力偏导仍然可以成立。
目标:计算 $\nabla_{\theta}\ell_{ce}(X\theta,y)$。
注意因为 $X\in \mathbb R^{m\times n}$,所以 $\theta$ 这回为了统一维度变成了矩阵右乘,显然 $\theta\in\mathbb R^{n\times k}$。
$$
\begin{aligned}
\frac{\partial}{\partial \theta} \ell_{ce}(X\theta,y) &= \frac{\partial \ell_{ce}(X\theta,y)}{\partial X\theta} \cdot \frac{\partial X\theta}{\partial \theta}\\
&= (Z-I_y)\cdot X
\end{aligned}
$$
这里 $Z-I_y\in\mathbb R^{m\times k}$,可以认为是 $m$ 个向量的堆叠;$X\in \mathbb R^{m\times n}$,因此我们要将这个结果按照维度重排为 $X^T\cdot(Z-I_y)$。
$$
\frac{\partial}{\partial \theta} \ell_{ce}(X\theta,y) = X^T\cdot(Z-I_y)
$$
MNIST
Python
这是一个linear hypothesis对于MNIST数据集分类算法的个人实现,测试集 acc = 0.92。
import loguru
import numpy as np
import gzip
from tqdm import tqdm
from copy import copy
def read_idx(filename):
with gzip.open(filename, 'rb') as f:
# 读取文件头(前16个字节)
data = f.read()
# 解析文件头信息
magic_number = int.from_bytes(data[0:4], byteorder='big')
if magic_number == 2051:
# 图像文件,读取图像数据
num_images = int.from_bytes(data[4:8], byteorder='big')
num_rows = int.from_bytes(data[8:12], byteorder='big')
num_cols = int.from_bytes(data[12:16], byteorder='big')
# 图像数据
images = np.frombuffer(data[16:], dtype=np.uint8).reshape(num_images, num_rows, num_cols)
return images
elif magic_number == 2049:
# 标签文件,读取标签数据
num_labels = int.from_bytes(data[4:8], byteorder='big')
labels = np.frombuffer(data[8:], dtype=np.uint8)
return labels
else:
raise ValueError("Unknown magic number")
image_file_tr = 'train-images-idx3-ubyte.gz'
image_file_ts = 't10k-images-idx3-ubyte.gz'
label_file_tr = 'train-labels-idx1-ubyte.gz'
label_file_ts = 't10k-labels-idx1-ubyte.gz'
class linear_model:
def __init__(self, n=784, k=10, lr=1e-3, batch_size=100):
self.n = n
self.k = k
self.lr = lr
self.eps = 1e-7
self.batch_size = batch_size
self.theta = np.random.randn(self.n, self.k).astype(np.float32)
def compute_loss(self, x, y):
# 1. 计算 softmax
# 为了避免溢出,减去每行的最大值(数值稳定性)
exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
exp_x += self.eps
softmax_probs = exp_x / np.sum(exp_x, axis=1, keepdims=True)
# 2. 获取每个样本的正确类别的预测概率
correct_probs = softmax_probs[np.arange(len(y)), y]
# 3. 计算交叉熵损失
loss = -np.mean(np.log(correct_probs))
return loss
def compute_gradient(self, x1, x2, y):
exp_x = np.exp(x2 - np.max(x2, axis=1, keepdims=True))
exp_x += self.eps
z = exp_x / np.sum(exp_x, axis=1, keepdims=True)
e_y = np.zeros((y.shape[0], self.k), dtype=np.float32)
e_y[np.arange(y.size), y] = 1
xt = x1.T.astype(np.float32)
g = np.matmul(xt, z - e_y)
return g
def forward(self, x, y, mode='train'):
input_x = copy(x)
x = x @ self.theta
if mode == 'train':
loss = self.compute_loss(x, y)
gradient = self.compute_gradient(input_x, x, y)
self.theta = self.theta - self.lr * gradient / self.batch_size
return x, loss
else:
return x
if __name__ == '__main__':
train_images = read_idx(image_file_tr)
train_labels = read_idx(label_file_tr)
test_images = read_idx(image_file_ts)
test_labels = read_idx(label_file_ts)
train_images = np.reshape(train_images, (train_images.shape[0], 28 * 28)).astype(np.float32)
test_images = np.reshape(test_images, (test_images.shape[0], 28 * 28)).astype(np.float32)
train_images = train_images / 255.0
test_images = test_images / 255.0
m = 10
epochs = 100
model = linear_model(n=784, k=10, lr=0.1, batch_size=m)
for e in range(epochs):
loguru.logger.info(f"Epoch {e+1}/{epochs}")
with tqdm(total=len(train_images) // m, desc=f"loss = {0}") as pbar:
loss_sum = np.zeros(1)
for i in range(len(train_images) // m):
x = train_images[i * m: (i + 1) * m]
y = train_labels[i * m: (i + 1) * m]
_, loss = model.forward(x, y)
loss_sum += loss
pbar.set_description(f"loss = {loss}")
pbar.update()
pbar.close()
loguru.logger.info(f"epoch {e+1}, average loss = {loss_sum / (len(train_images) // m)}")
preds = model.forward(test_images, test_labels, 'test')
preds = np.argmax(preds, axis=1)
acc = np.sum(preds == test_labels) / len(test_labels)
loguru.logger.info(f"accuracy = {acc}")
if (e + 1) % 2 == 0:
model.lr *= 0.9Cpp
cpp实现移植于dlsys hw0,因为使用指针和vector互相转换,所以有很多拷贝,效率不高。
#include <bits/stdc++.h>
using std::vector;
template<typename ...T>
auto print(T&&... args) {
((std::cout << args << " "), ...) << "\n";
}
template<typename T> struct matrix {
size_t n, m;
vector<vector<T>> a;
matrix(size_t n_, size_t m_, int val = 0) : n(n_), m(m_), a(n_, vector<T>(m_, val)) {}
matrix(const T* x, size_t n_, size_t m_) {
n = n_, m = m_;
a.resize(n, vector<T>(m));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = *(x + i * m + j);
}
}
}
vector<T>& operator[](int k) { return this->a[k]; }
matrix operator - (matrix& k) { return matrix(*this) -= k; }
matrix operator * (matrix& k) { return matrix(*this) *= k; }
matrix& operator -=(matrix& mat) {
assert(n == mat.n);
assert(m == mat.m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] -= mat[i][j];
}
}
return *this;
}
matrix& operator *= (matrix& mat) {
assert(m == mat.n);
int x = n, y = mat.m, z = m;
matrix<T> c(x, y);
for (int i = 0; i < x; i++) {
for (int k = 0; k < z; k++) {
T r = a[i][k];
for (int j = 0; j < y; j++) {
c[i][j] += mat[k][j] * r;
}
}
}
return *this = c;
}
matrix<T> transpose() {
matrix<T> result(m, n);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
result[i][j] = a[j][i];
}
}
return result;
}
matrix<float> softmax() {
matrix<float> result(*this);
for (int i = 0; i < n; i++) {
auto& v = result.a[i];
auto mx = *std::max_element(v.begin(), v.end());
for (auto& j : v) {
j -= mx;
j = std::exp(j);
}
auto exp_sum = std::accumulate(v.begin(), v.end(), (float)0.0);
for (auto& j : v) {
j /= exp_sum;
}
}
return result;
}
};
float ce_loss(matrix<float>& Z, matrix<uint8_t>& I_y) {
int batch = Z.n;
float sum = 0;
for (int i = 0; i < batch; i++) {
float v = Z[i][I_y[i][0]];
v = -std::log(v);
sum += v;
}
return sum / static_cast<float>(batch);
}
float softmax_regression_epoch_cpp(const float* X, const unsigned char* y,
float* theta, size_t m, size_t n, size_t k,
float lr, size_t batch)
{
/**
* A C++ version of the softmax regression epoch code. This should run a
* single epoch over the data defined by X and y (and sizes m,n,k), and
* modify theta in place. Your function will probably want to allocate
* (and then delete) some helper arrays to store the logits and gradients.
*
* Args:
* X (const float *): pointer to X data, of size m*n, stored in row
* major (C) format
* y (const unsigned char *): pointer to y data, of size m
* theta (float *): pointer to theta data, of size n*k, stored in row
* major (C) format
* m (size_t): number of examples
* n (size_t): input dimension
* k (size_t): number of classes
* lr (float): learning rate / SGD step size
* batch (int): SGD minibatch size
*
* Returns:
* (None)
*/
/// BEGIN YOUR CODE
float alpha = lr / static_cast<float>(batch);
float loss = 0;
for (int e = 0; e < m / batch; e++) {
matrix<float> batch_X(X + e * batch * n, batch, n);
matrix<unsigned char> batch_y(y + e * batch, batch, 1);
matrix<float> t(theta, n, k);
auto&& XW = batch_X * t;
auto&& XT = batch_X.transpose();
auto&& Z = XW.softmax();
matrix<float> I_y(batch, k);
auto loss_i = ce_loss(Z, batch_y);
loss += loss_i;
// X^T @ (Z - I_y)
for (int i = 0; i < batch; i++) {
I_y[i][batch_y[i][0]] = 1;
}
Z -= I_y;
auto&& res = XT * Z;
for (int i = 0; i < n; i++) {
for (int j = 0; j < k; j++) {
*(theta + i * k + j) -= res[i][j] * alpha;
}
}
}
return loss / (m / batch);
/// END YOUR CODE
}
float predict(const float* X, const unsigned char* y, const float* theta, size_t m, size_t n, size_t k) {
matrix<float> MX(X, m, n);
matrix<float> W(theta, n, k);
auto&& res = MX * W;
int num_acc = 0;
for (int i = 0; i < m; i++) {
auto&& v = res.a[i];
int pred_class = max_element(v.begin(), v.end()) - v.begin();
int tp = *(y + i);
num_acc += (pred_class == tp);
}
return static_cast<float>(num_acc) / m;
}
uint32_t swap_endian(uint32_t val) {
return ((val >> 24) & 0x000000FF) | // 获取最高字节
((val >> 8) & 0x0000FF00) | // 获取次高字节
((val << 8) & 0x00FF0000) | // 获取次低字节
((val << 24) & 0xFF000000); // 获取最低字节
}
void read_mnist_images(const std::string& filepath, std::vector<std::vector<uint8_t>>& images, int& num_images, int& rows, int& cols) {
std::ifstream file(filepath, std::ios::binary);
uint32_t magic_number, num_items;
uint32_t num_rows, num_cols;
file.read(reinterpret_cast<char*>(&magic_number), 4);
magic_number = swap_endian(magic_number); // 转换字节序(小端 -> 大端)
file.read(reinterpret_cast<char*>(&num_items), 4);
num_items = swap_endian(num_items);
file.read(reinterpret_cast<char*>(&num_rows), 4);
num_rows = swap_endian(num_rows);
file.read(reinterpret_cast<char*>(&num_cols), 4);
num_cols = swap_endian(num_cols);
num_images = num_items;
rows = num_rows;
cols = num_cols;
images.resize(num_images, std::vector<uint8_t>(rows * cols));
for (int i = 0; i < num_images; ++i) {
file.read(reinterpret_cast<char*>(images[i].data()), rows * cols);
}
}
void read_mnist_labels(const std::string& filepath, std::vector<uint8_t>& labels, int& num_labels) {
std::ifstream file(filepath, std::ios::binary);
// 读取头部信息
uint32_t magic_number, num_items;
file.read(reinterpret_cast<char*>(&magic_number), 4);
magic_number = swap_endian(magic_number); // 转换字节序(小端 -> 大端)
file.read(reinterpret_cast<char*>(&num_items), 4);
num_items = swap_endian(num_items);
num_labels = num_items;
labels.resize(num_labels);
// 读取所有标签数据
file.read(reinterpret_cast<char*>(labels.data()), num_labels);
}
float* convert_vec(const std::vector<std::vector<uint8_t>>& images_tr) {
size_t num_images = images_tr.size();
if (num_images == 0)
return nullptr;
size_t image_size = images_tr[0].size();
float* flattened = new float[num_images * image_size];
for (size_t i = 0; i < num_images; i++) {
const std::vector<uint8_t>& img = images_tr[i];
for (size_t j = 0; j < image_size; j++) {
flattened[i * image_size + j] = static_cast<float>(img[j]) / 255.0;
}
}
return flattened;
}
uint8_t* convert_vec(const std::vector<uint8_t>& images_tr) {
size_t num_images = images_tr.size();
if (num_images == 0)
return nullptr;
uint8_t* flattened = new uint8_t[num_images];
for (size_t i = 0; i < num_images; i++) {
flattened[i] = images_tr[i];
}
return flattened;
}
std::mt19937 rng(114);
float generateRandomNumber() {
std::normal_distribution<float> distribution(0.0f, 1.0f);
return distribution(rng);
}
void solve(std::vector<std::vector<uint8_t>>& images_tr, std::vector<std::vector<uint8_t>>& images_ts,
std::vector<uint8_t>& labels_tr, std::vector<uint8_t> labels_ts) {
int num_samples = images_tr.size();
int batch_size = 50;
int epochs = 10;
float* train_images = convert_vec(images_tr);
float* test_images = convert_vec(images_ts);
uint8_t* train_labels = convert_vec(labels_tr);
uint8_t* test_labels = convert_vec(labels_ts);
int m = 60000;
int n = 784;
int k = 10;
float lr = 0.2;
float* theta = new float[n * k];
for (int i = 0; i < n * k; i++) {
theta[i] = generateRandomNumber();
}
int tm = 10000;
for (int e = 0; e < epochs; e++) {
auto loss = softmax_regression_epoch_cpp(train_images, train_labels, theta, m, n, k, lr, batch_size);
auto acc = predict(test_images, test_labels, theta, tm, n, k);
print("Epoch", e + 1, "| loss =", loss, "| acc =", acc);
}
}
int main() {
// 注意这里要解压文件
std::string images_path_tr = "train-images-idx3-ubyte";
std::string images_path_ts = "t10k-images-idx3-ubyte";
std::string labels_path_tr = "train-labels-idx1-ubyte";
std::string labels_path_ts = "t10k-labels-idx1-ubyte";
int num_images_tr, num_labels_tr, rows, cols;
int num_images_ts, num_labels_ts;
std::vector<std::vector<uint8_t>> images_tr, images_ts;
std::vector<uint8_t> labels_tr, labels_ts;
read_mnist_images(images_path_tr, images_tr, num_images_tr, rows, cols);
read_mnist_images(images_path_ts, images_ts, num_images_ts, rows, cols);
read_mnist_labels(labels_path_tr, labels_tr, num_labels_tr);
read_mnist_labels(labels_path_ts, labels_ts, num_labels_ts);
solve(images_tr, images_ts, labels_tr, labels_ts);
}