直线

定义

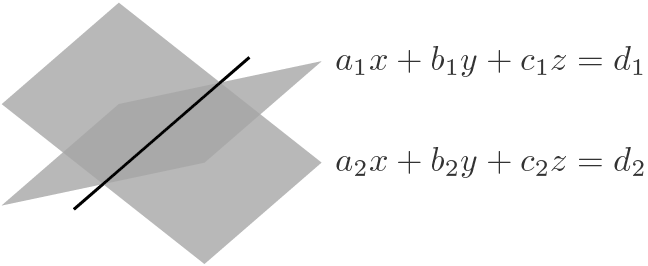
一般式

不像二维几何中，直线 $l$ 可以直接用一个方程 $ax+by=c$ 简单地表示，三维几何中 $ax+by+cz=d$ 表示一个平面。而直线可以表示为两个平面的交，即方程组

$$
l:\begin{cases}
\Pi_1: a_1x+b_1y+c_1z=d_1\\
\Pi_2: a_2x+b_2y+c_2z=d_2\\
\end{cases}
$$

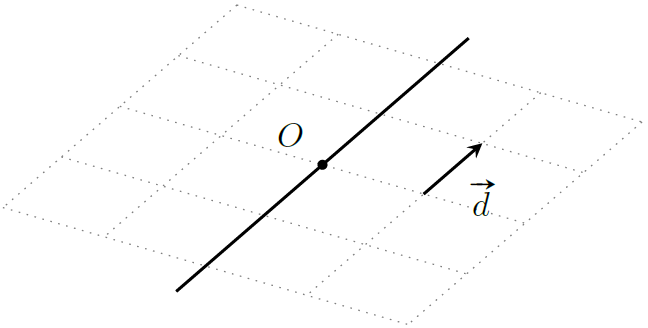
点向式

跟二维几何类似的是，一条直线也可以由直线上一点 $O$ 和直线的方向向量 $\boldsymbol d$ 表示
$$
l:O + t\boldsymbol d
$$
这里 $t$ 是参数方程中的参数，可以取任意实数。相较于一般式，点向式是三维直线更简洁、更直观的表示方法。

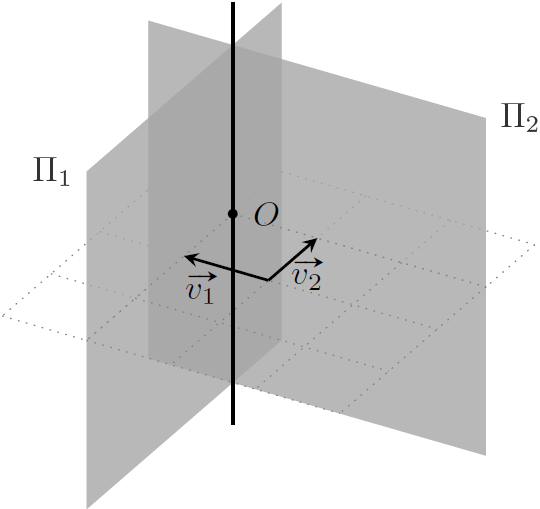
一般式转换为点向式

因为直线 $l$ 既在平面 $\Pi_1$ 上，又在平面 $\Pi_2$ 上，所以直线 $l$ 的方向向量 $\boldsymbol d$ 同时垂直于两平面的法向量 $\boldsymbol n_1,\boldsymbol n_2$，所以有 $\boldsymbol d = \boldsymbol n_1\times \boldsymbol n_2$。

然后，我们就只需要找到直线 $l$ 上任意一点 $O$ 的坐标。这里，我们将计算出 $l$ 上最接近原点的一点，公式如下
$$
O = \frac{(d_1\boldsymbol n_2 – d_2\boldsymbol n_1)\times \boldsymbol d}{|\boldsymbol d|^2}
$$
我们来分析一下这个公式，该式由两个向量相减得到，
$$
\begin{aligned}
\boldsymbol v_1 &= \frac{d_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\\
\boldsymbol v_2 &= \frac{d_2}{|\boldsymbol d|^2}(\boldsymbol n_1\times\boldsymbol d)\\
\end{aligned}
$$
显然，$\boldsymbol v_1$ 是垂直于 $\boldsymbol n_2$（平行于 $\Pi_2$）的向量，$\boldsymbol v_2$ 是垂直于 $\boldsymbol n_1$（平行于 $\Pi_1$）的向量。因此，$\boldsymbol v_1$ 可以被视作是从原点出发，以平行于 $\Pi_2$ 的方向指向平面 $\Pi_1$ 的向量；$v_2$ 则是从原点出发，以平行于 $\Pi_1$ 的方向指向平面 $\Pi_2$ 的向量。

然后，我们验证点 $O$ 在平面 $\Pi_1$ 上

$$
\begin{aligned} \boldsymbol n_1\cdot O &= \boldsymbol n_1\cdot(\boldsymbol v_1+\boldsymbol v_2)\\ &= \boldsymbol n_1\cdot\boldsymbol v_1\\ &= \frac{d_1\boldsymbol n_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\\ &= \frac{d_1\boldsymbol d}{|\boldsymbol d|^2}(\boldsymbol n_1\times\boldsymbol n_2)\quad(三重积性质)\\ &= \frac{d_1\boldsymbol d}{|\boldsymbol d|^2}\cdot\boldsymbol d\\ &=d_1 \end{aligned}
$$

同理可证明点 $O$ 也在平面 $\Pi_2$ 上。此外，还可证明 $\boldsymbol v_1\perp \boldsymbol d$

$$
\begin{aligned} \boldsymbol v_1\times\boldsymbol d &= \frac{d_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\cdot \boldsymbol d\\ &= \frac{d_1}{|\boldsymbol d|^2}\boldsymbol n_2\cdot(\boldsymbol d\times\boldsymbol d)\\ &= \boldsymbol 0 \end{aligned}
$$

同理可证明 $\boldsymbol v_2\perp\boldsymbol d$，于是点 $O$ 是直线 $l$ 上距离原点最近的一点。

点和直线

位置关系

假设我们需要验证某一点 $P$ 是否位于直线 $l:O+t\boldsymbol d$ 上，实际上只需要证明 $\vec{OP}$ 平行于 $\boldsymbol d$，也就是 $\boldsymbol d\times\vec{OP}=\boldsymbol 0$。

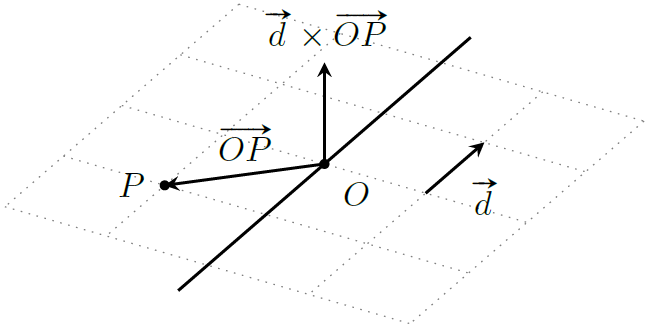
此外，$\boldsymbol d\times\vec{OP}$ 还可以用于计算点 $P$ 到直线 $l$ 的距离（叉积的绝对值等于平行四边形面积）
$$
\text{dist}_l P = \frac{|\boldsymbol d\times\vec{OP}|}{|\boldsymbol d|}
$$

投影点/反射点

如下图，作点 $P$ 关于直线 $l$ 的投影点 $P^\prime$。

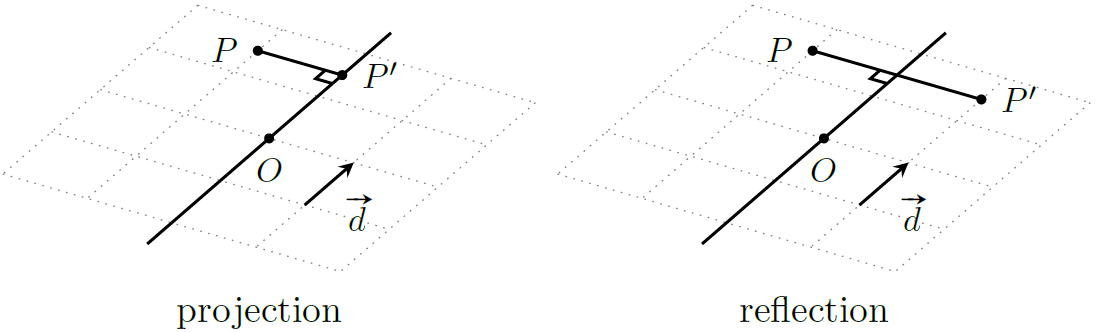
根据点积的性质有 $\vec{OP}\cdot \frac{\boldsymbol d}{|\boldsymbol d|}=|OP^\prime|$，所以

$$
\begin{aligned} \text{proj}_lP &= O + |OP^\prime|\cdot \frac{\boldsymbol d}{|\boldsymbol d|}\\ &= O + \vec{OP}\cdot\frac{\boldsymbol d}{|\boldsymbol d|}\cdot\frac{\boldsymbol d}{|\boldsymbol d|}\\ &= O + \frac{\vec{OP}\cdot \boldsymbol d\cdot\boldsymbol d}{|\boldsymbol d|^2} \end{aligned}
$$

反射点 $\text{refl}_lP$ 可以通过投影点求出

$$
\text{refl}_lP = P + 2(\text{proj}_lP-P)
$$

平面和直线

位置关系

设平面 $\Pi:\boldsymbol n\cdot P=d$，直线 $l:O+t\boldsymbol d$。如果平面 $\Pi$ 上某一点 $P$ 同时也是直线 $l$ 上一点，则有
$$
\boldsymbol n\cdot(O+t\boldsymbol d) = d
$$

然后解出参数 $t$

$$
t = \frac{d-\boldsymbol n\cdot O}{\boldsymbol n\cdot\boldsymbol d} = \frac{-\text{side}_\Pi O}{\boldsymbol n\cdot\boldsymbol d}
$$
因此直线与平面的交点就是

$$
O + t\boldsymbol d = O – \frac{\text{side}_\Pi O}{\boldsymbol n\cdot\boldsymbol d}\cdot\boldsymbol d
$$

除了直线与平面相交的情况，直线还有可能平行于平面，此时直线的方向向量必然垂直于平面的法向量，即

$$
\boldsymbol d \cdot\boldsymbol n = 0
$$

投影直线/反射直线

线面角

类似于二面角，直线 $l$ 和平面 $\Pi$ 的线面角实际上就是方向向量 $\boldsymbol d$ 和法向量 $\boldsymbol n$ 之间的夹角 $\theta$。

根据余弦定理有
$$
\theta = \arccos(\frac{\boldsymbol n\cdot\boldsymbol d}{|\boldsymbol n||\boldsymbol d|})
$$
此外，$\theta$ 的范围一般也是取 $[0,\frac{\pi}{2}]$。

线线角

两条直线之间的夹角实际上就是由两条直线的方向向量定义的，计算类似于线面角或二面角。

直线和直线

直线与直线之间可能有以下三种情况：

1. 平行
2. 相交
3. 偏离

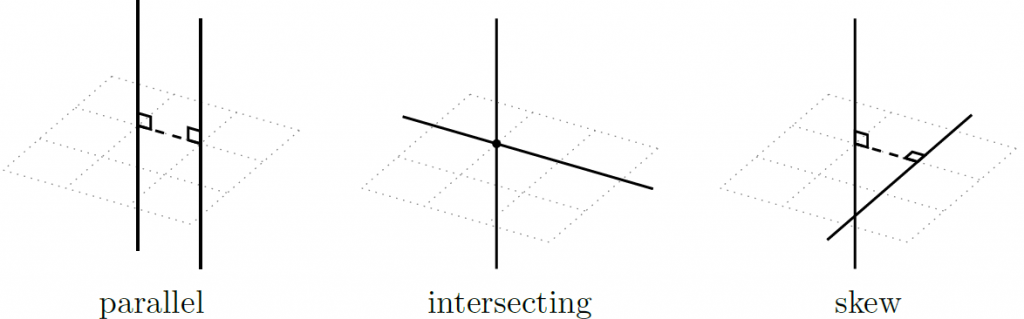
下文中，我们将讨论两直线 $l_1:O_1+k\boldsymbol d_1$ 和 $l_2:O_2+t\boldsymbol d_2$ 之间的关系。

平行

首先，两直线平行是最简单的一种情况，只需要判断两条直线之间的方向向量是否平行，即
$$
\boldsymbol d_1\times \boldsymbol d_2 = \boldsymbol 0
$$
如果两直线平行，则它们之间的距离就是点 $O_1$ 到直线 $l_2$ 的距离。

非平行

设点 $C_1$ 是直线 $l_1$ 上最接近直线 $l_2$ 的点，点 $C_2$ 是直线 $l_2$ 上最接近直线 $l_1$ 的点，那么线段 $C_1C_2$ 必然同时垂直于 $l_1,l_2$，且 $|C_1C_2|$ 就是两直线之间的最短距离。设 $\boldsymbol n = \boldsymbol d_1\times \boldsymbol d_2$，因为向量 $\vec{C_1C_2}$ 同时垂直于 $\boldsymbol d_1,\boldsymbol d_2$，所以 $\vec{C_1C_2}\parallel \boldsymbol n$，于是

$$
\text{dist}_{l_1}l_2 = |C_1C_2| = \frac{|\vec{C_1C_2}\cdot\boldsymbol n|}{|\boldsymbol n|}
$$

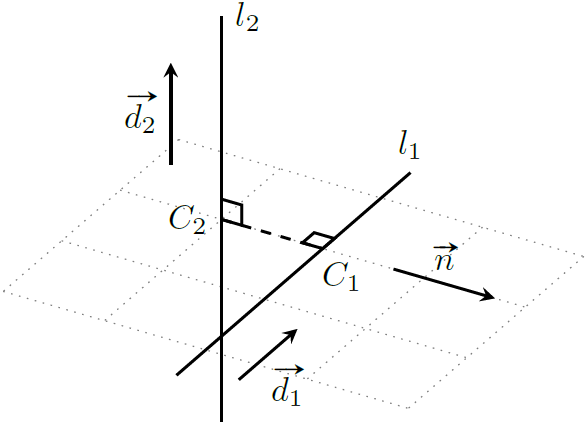
但是我们还不知道 $C_1,C_2$ 的坐标，无法求解上式，因此我们需要将问题进一步转化：考虑到点积的性质（向量之间的投影不变，则向量点积的值不变），$\vec{C_1C_2}\cdot \boldsymbol n$ 式中可以将点 $C_2$ 移动至直线 $l_2$ 上任意一点 $C_2^\prime$ 而不影响该式的值，即 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{C_1C_2^\prime}\cdot \boldsymbol n$。为了方便起见，我们取点 $C_2^\prime = O_2$，即 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{C_1O_2}\cdot \boldsymbol n$。同理点 $C_1$ 也可以移动至直线 $l_1$ 上任意一点 $C_1^\prime$，取点 $C_1^\prime=O_1$，于是 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{O_1O_2}\cdot \boldsymbol n$，

$$
\text{dist}_{l_1}l_2 = \frac{|\vec{O_1O_2}\cdot\boldsymbol n|}{|\boldsymbol n|}
$$

实际上点 $C_1,C_2$ 的坐标也是可以求的：设直线 $l_2$ 和向量 $\boldsymbol n$ 张开的平面为 $\Pi_2$，此时点 $C_1$ 实际上就是平面 $\Pi_2$ 和直线 $l_1$ 之间的交点。

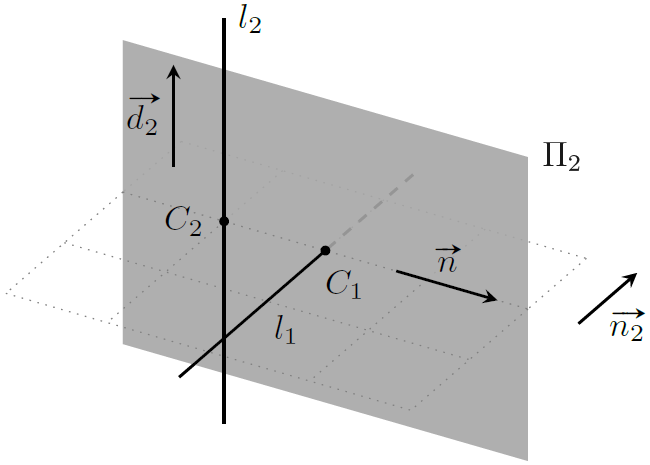
即 $\Pi_2$ 的法向量为 $\boldsymbol n_2 = \boldsymbol d_2\times\boldsymbol n$，利用直线平面之间的距离公式即可求出
$$
C_1 = O_1 + \frac{\vec{O_1O_2}\cdot\boldsymbol n_2}{\boldsymbol d_1\cdot\boldsymbol n_2}\cdot\boldsymbol d_1
$$
特别地，当 $l_1,l_2$ 相交时，$C_1,C_2$ 是同一个点（$l_1,l_2$ 的交点）。

线段

点和线段

要求点 $P$ 到线段 $AB$ 的最短距离，实际上就是判断点 $P$ 到直线 $AB$ 的投影点 $H$ 是否位于线段 $AB$ 内。如果是，则最短距离就是 $|PH|$；如果不是，则最短距离就是 $\min(|PA|, |PB|)$。

此外，也可以通过直接求点 $P$ 到线段 $AB$ 的最近点得到答案，先求出点 $P$ 到直线 $AB$ 的投影点 $H$，然后求出 $t = (\vec{AH}\cdot \vec{AB}) / (\vec{AB}\cdot\vec{AB})$，然后将 $t$ clamp到区间 $[0,1]$ 内，则 $A+t\cdot \vec{AB}$ 就是点 $P$ 到线段 $AB$ 的最近点。

线段和线段

三维空间中，线段 $AB$ 和 $CD$ 之间的最短距离是一个相对复杂的问题，但实际上也有非常漂亮的解决办法，下面介绍的方法来源于这里。

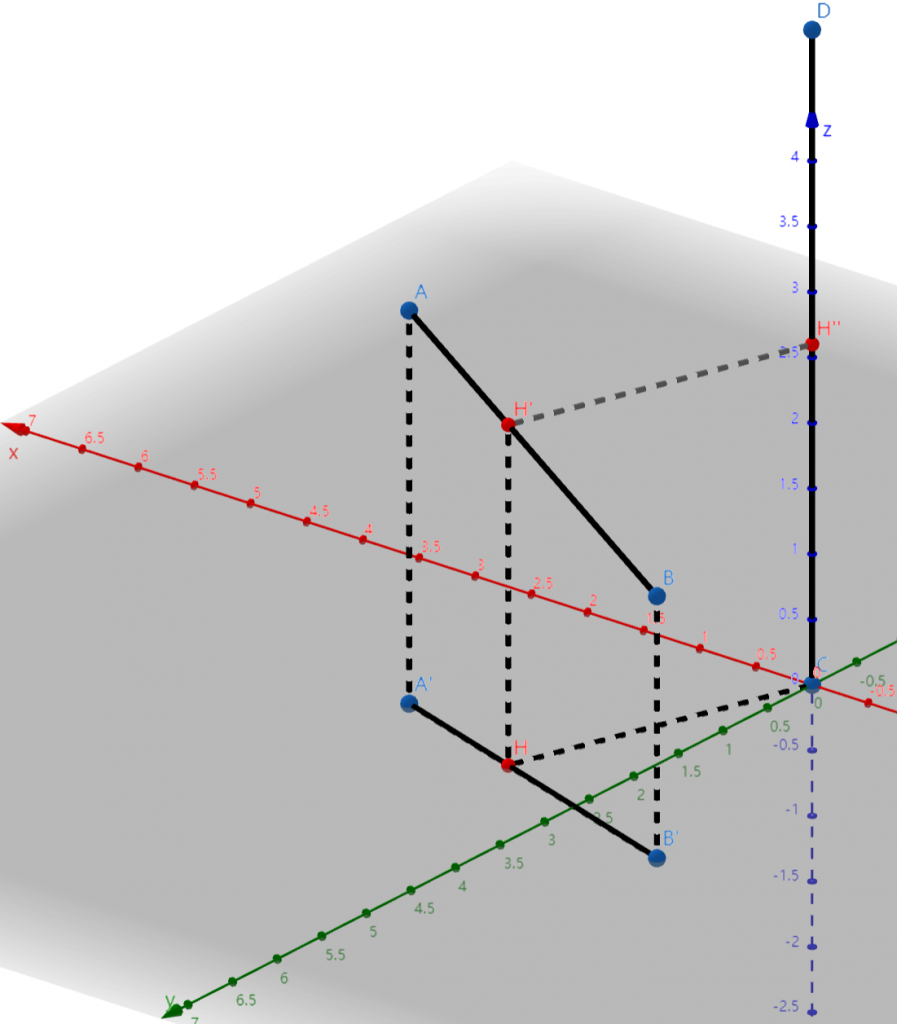
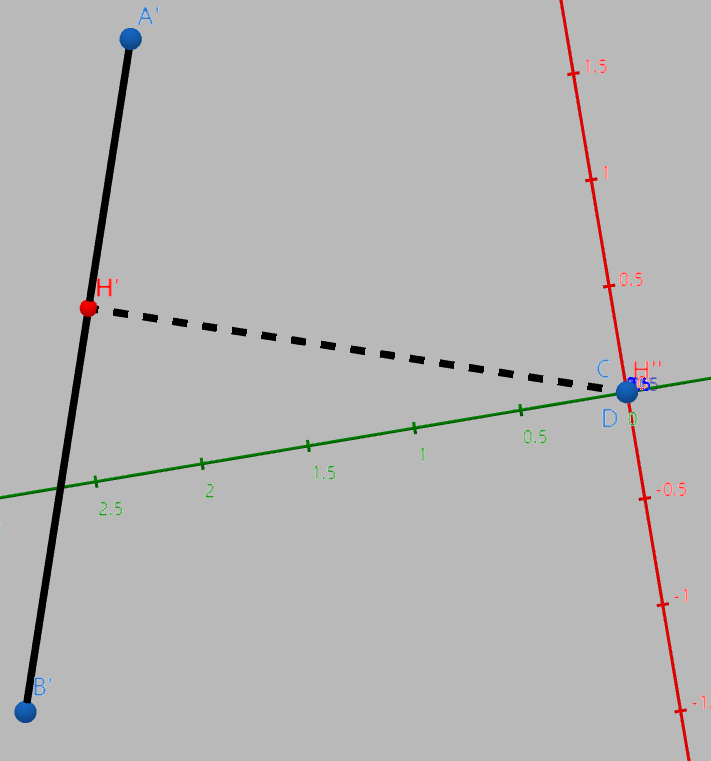
如图，我们先构建一个由法向量 $\vec{CD}$ 和点 $C$ 定义的平面 $\Pi$（上图中的 $xOy$ 平面），然后将线段 $AB$ 投影到该平面上，投影线段为 $A^\prime B^\prime$。找到点 $C$ 到线段 $A^\prime B^\prime$ 的最近点 $H$，再作 $HH^\prime \parallel AA^\prime$。

此时，线段 $AB$ 和 $CD$ 之间的最短距离就是点 $H^\prime$ 到线段 $CD$ 的最短距离（图中的 $|H^\prime H^{\prime\prime}|$）。这个方法的核心思路是：如果我们沿着 $\vec{DC}$ 方向从上向下看，那么线段 $AB$ 和 $CD$ 之间的最短距离就被转化为了点 $C$ 到线段 $AB$ 之间的距离（因为此时线段 $CD$ 退化为了一个点）。

当然，你也可以用前文提到的计算直线之间最近点对，然后判断点对是否分别在线段上进行计算。