点和向量

叉积

与二维向量叉积不同，三维向量叉积是一个向量，向量 $\boldsymbol a=(x1,y1,z1)$ 叉乘 $\boldsymbol b=(x2,y2,z2)$ 的计算公式如下

$$\begin{aligned} (x1,y1,z1)\times (x2,y2,z2) &= \det \begin{bmatrix} \boldsymbol i & \boldsymbol j & \boldsymbol k\\ x1 & y1 & z1\\ x2 & y2 & z2\\ \end{bmatrix}\\ &= (y1\cdot z2 – z1\cdot y2, z1\cdot x2 – x1\cdot z2, x1\cdot y2 – y1\cdot x2) \end{aligned}$$

该向量的方向满足右手定则（Right-hand rule），垂直于向量 $\boldsymbol a, \boldsymbol b$ 所在平面

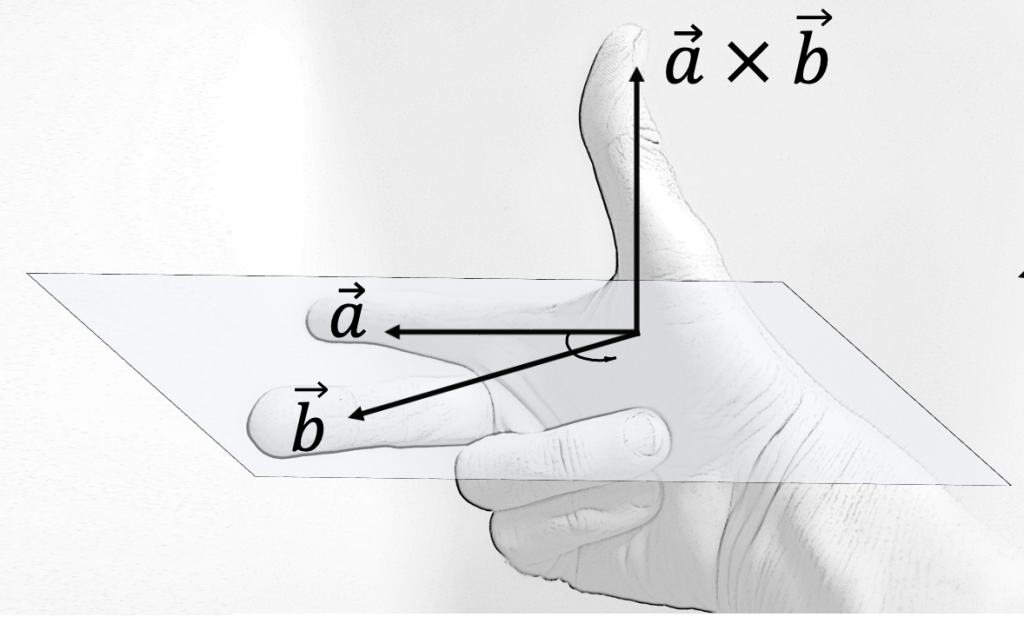
由于三维叉积的特殊性质，它常被用于计算平面法向量。

标量三重积

标量三重积（Scalar triple product），也称为混合积，是一种三个三维向量同时进行点积和叉积的计算，定义如下

$$(\boldsymbol u\times \boldsymbol v)\cdot \boldsymbol w$$

根据对称性可以得到 $\boldsymbol u\cdot (\boldsymbol v\times \boldsymbol w) = \boldsymbol v\cdot (\boldsymbol w\times \boldsymbol u)= \boldsymbol w\cdot (\boldsymbol u\times \boldsymbol v)=-\boldsymbol u\cdot (\boldsymbol w\times \boldsymbol v)$。

三重积可以用于判断某个向量相对于某一平面的方向（判断该向量的方向指向平面之上或平面之下）。

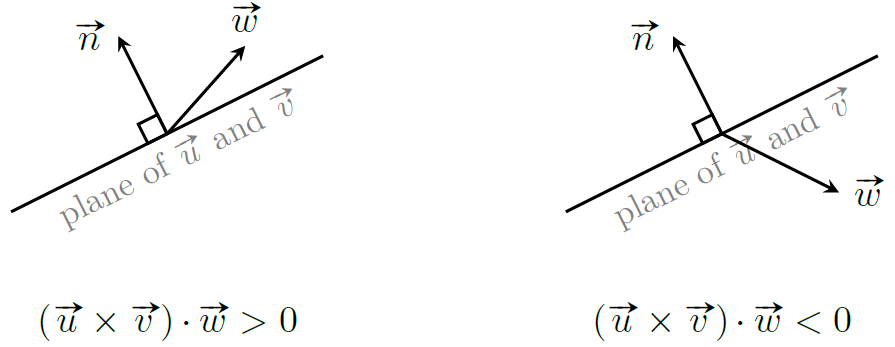
如图，若 $(\boldsymbol u\times \boldsymbol v)\cdot \boldsymbol w\gt 0$，则向量 $\boldsymbol w$ 指向 $uv$ 平面上方，否则指向 $uv$ 平面下方。

仿射变换

这一节大部分内容来源于我的图形学课程笔记，符号定义与本文稍有不同：

• $\vec v$ 表示向量 $v$。
• $\overset {\sim}{p}$ 表示点 $p$（坐标）。
• $\mathcal {L}$ 表示一个线性变换。

线性变换

线性变换 $\mathcal {L}$ 的性质为

1. $\mathcal{L}(\vec v + \vec u) = \mathcal{L}(\vec v) + \mathcal{L}(\vec u)$
2. $\mathcal{L}(a\vec v) = a\mathcal{L}(\vec v)$
3. $\mathcal{L}(\vec 0) = \vec 0$
4. 向量 $\vec v$ 经过线性变换后仍然是一个向量。$\vec v\Rightarrow \mathcal {L}(\vec v)$。

根据线性变换的性质可知

$$\mathcal{L}(\vec v) = \mathcal{L}(\sum_{i}c_i\vec {b_i}) = \sum_{i} c_i\mathcal{L}(\vec{b_i})$$

这里，$(\vec {b_1},\vec {b_2},\cdots,\vec {b_n})$ 表示线性空间的一组基，$\vec v = \sum_{i} c_i\vec {b_i}$ 就是这组基的一个线性组合（或者说 ($c_1,c_2,\cdots,c_n$) 就是该向量在这组基下的坐标）。我们将上式写成矩阵形式（以三维空间为例）

$$\mathcal{L}(\vec v) = \pmatrix{\mathcal{L}(\vec b_1) & \mathcal{L}(\vec{b_2}) & \mathcal{L}(\vec{b_3})}\pmatrix{c_1\\c_2\\c_3}$$

这里 $\mathcal {L}(\vec {b_i})$ 是一个向量，也可以表示为矩阵形式

$$\mathcal{L}(\vec{b_i}) = \pmatrix{\vec{b_1} & \vec{b_2} & \vec{b_3}}\pmatrix{M_{1,i}\\ M_{2,i}\\ M_{3,i}}$$

这里 $M_{1,i},M_{2,i},M_{3,i}$ 表示线性变换 $\mathcal {L}$ 的参数。根据上方推导即可得到

$$\begin{aligned} \mathcal{L}(\vec v) &= \pmatrix{\mathcal{L}(\vec b_1) & \mathcal{L}(\vec{b_2}) & \mathcal{L}(\vec{b_3})}\pmatrix{c_1\\c_2\\c_3}\\ &= \pmatrix{\vec{b_1} & \vec{b_2} & \vec{b_3}}\pmatrix{M_{1,1}&M_{1,2}&M_{1,3}\\ M_{2,1}&M_{2,2}&M_{2,3}\\ M_{3,1}&M_{3,2}&M_{3,3}}\pmatrix{c_1\\c_2\\c_3}\\ &= \vec{\textbf{b}^T}\textbf{M}\textbf{c} \end{aligned}$$

基变换

假设我们有两组基 $\vec {\mathbf {a}}, \vec {\mathbf {b}}$，并且

$$\vec{a_i} = \pmatrix{\vec{b_1} & \vec{b_2} &\vec{b_3}}\pmatrix{M_{1,i}\\M_{2,i}\\M_{3,i}}$$

简记作 $\vec {\mathbf {a}^T} = \vec {\mathbf {b}^T}\mathbf {M}$。

此时，对于一个向量 $\vec v = \vec {\mathbf {b}^T} \mathbf c$，它在基 $\vec {\mathbf {a}}$ 下的坐标就是 $\vec {\mathbf {a}^T}\mathbf {M}^{-1}\mathbf {c}$。

齐次坐标

在计算机图形学中，坐标系经常定义为原点 $\overset {\sim}{o}$ 加上一组基 $\vec {\mathbf {b}}$，于是空间中的任意一个点 $\overset {\sim}{p}$ 就可以表示为

$$\overset{\sim}{p} = \overset{\sim}{o} + \vec{v} = \overset{\sim}{o} + \sum_{i}c_i\vec{b_i}$$

注意到，上式也可以写成矩阵形式（以三维空间为例）：

$$\overset{\sim}{p} = \overset{\sim}{o} + \sum_{i}c_i\vec{b_i} = \pmatrix{\vec{b_1} & \vec{b_2} & \vec{b_3} & \overset{\sim}{o}} \pmatrix{c_1\\ c_2\\ c_3\\ 1}$$

这里，我们将一个三维的坐标 $(c_1,c_2,c_3)^T$ 拓展到了四维 $(c_1,c_2,c_3,1)^T$，这第四个维度就被称为是虚拟坐标（dummy coordinate），目前它的取值始终是 $1$。这种四维的坐标表示被称为是齐次坐标（Homogeneous coordinates）。

引入了坐标系原点后的线性变换可以表示为：

$$\overset{\sim}{o}+\sum_{i=1}^3 c_i\mathcal{L}(\vec{b_i}) = \pmatrix{\vec{b_1}&\vec{b_2}&\vec{b_3}&\overset{\sim}{o}} \pmatrix{M_{1,1}&M_{1,2}&M_{1,3}&0\\ M_{2,1}&M_{2,2}&M_{2,3}&0\\ M_{3,1}&M_{3,2}&M_{3,3}&0\\ 0&0&0&1\\} \pmatrix{c_1\\ c_2\\ c_3\\ 1}$$

仿射变换

简单地说，仿射变换就是线性变换 + 平移变换。我们知道线性变换都可以用三维的矩阵乘法表示，而平移变换并不行（一般而言，平移变换就是向量加法），但是当我们引入了虚拟坐标后，平移变换就可以用四维矩阵乘法来表示了。

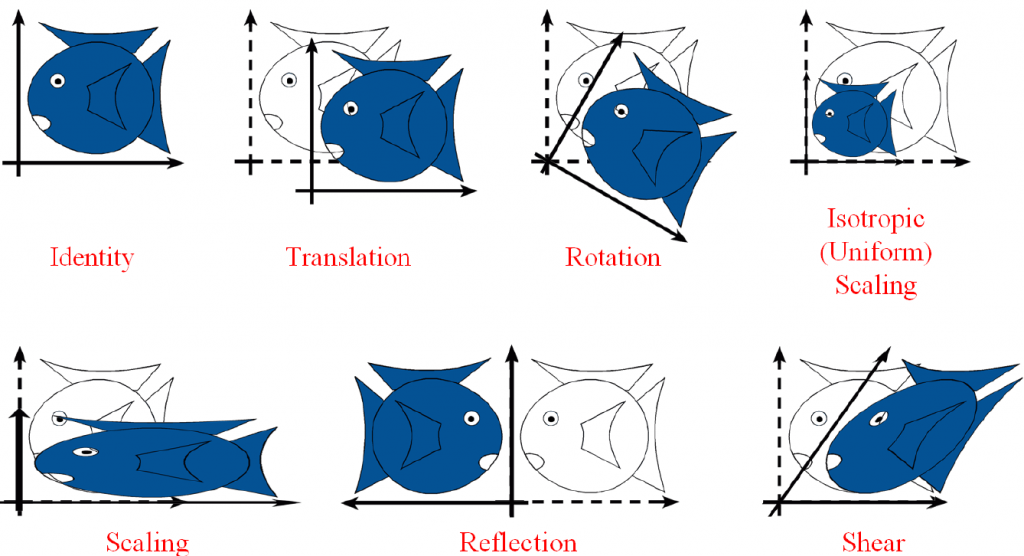
平移 (Translation)

对于一个平移变换 $\overset {\sim}{p}\Rightarrow \overset {\sim}{p} + \vec v$，这里平移向量 $\vec v$ 显然可以用基 $\vec {\mathbf {b}}$ 表示为

$$\vec v = \pmatrix{\vec{b_1}&\vec{b_2}&\vec{b_3}} \pmatrix{M_{1,4}\\M_{2,4}\\M_{3,4}}$$

这里 $\pmatrix {M_{1,4}\\M_{2,4}\\M_{3,4}}$ 就是向量 $\vec v$ 在基 $\vec {\mathbf {b}}$ 下的坐标，因此平移变换可以看作是原点 $\overset {\sim}{o}$ 变成了 $\overset {\sim}{o}+\vec v$：

$$\overset{\sim}{o}+\vec v + \sum_{i=1}^3 c_i\vec{b_i} =\pmatrix{\vec{b_1}&\vec{b_2}&\vec{b_3}&\overset{\sim}{o}}\pmatrix{1&0&0&M_{1,4}\\0&1&0&M_{2,4}\\0&0&1&M_{3,4}\\0&0&0&1\\}\pmatrix{c_1\\c_2\\c_3\\1}$$

伸缩 (Scaling)

对于一个伸缩变换，实际上就是基向量的模长改变了（可能还有方向），因此变换矩阵为

$$\textbf{M} = \pmatrix{s_x&0&0&0\\ 0&s_y&0&0\\ 0&0&s_z&0\\ 0&0&0&1}$$

这里 $s_x,s_y,s_z$ 表示三个基向量的伸缩倍率。

旋转 (Rotation)

首先，在三维空间中，旋转往往被表述为向量 $\boldsymbol P$ 绕某一旋转轴 $\boldsymbol A$ 旋转 $\theta$ 角，注意到向量旋转具有方向性，因此我们规定：沿着旋转轴 $\boldsymbol A$ 的负方向向正方向看去，逆时针旋转对应的角度为正。

首先回顾二维平面中的旋转，设 $\boldsymbol P=(x,y)$，$\boldsymbol Q$ 是向量 $\boldsymbol P$ 逆时针旋转 $90^\circ$ 得到的向量，即 $(-y,x)$。此时 $\boldsymbol P,\boldsymbol Q$ 构成一组正交基，我们可以用这组正交基表示平面中的任意一个向量 $\boldsymbol P^\prime$。

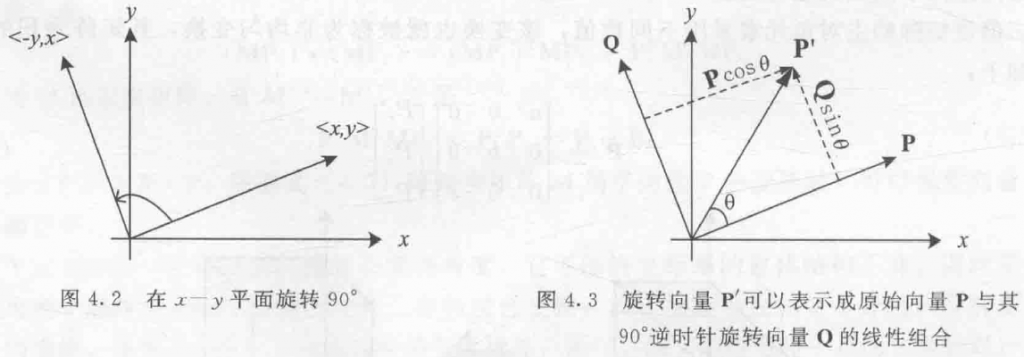
设向量 $\boldsymbol P$ 逆时针旋转 $\theta$ 角后得到向量 $\boldsymbol P^\prime$，此时 $\boldsymbol P^\prime$ 可以分解为 $\boldsymbol P\cos\theta + \boldsymbol Q\sin\theta$，该向量的两个分量为

$$\begin{cases} P_x^\prime = x\cos\theta – y\sin\theta\\ P_y^\prime = y\cos\theta+x\sin\theta \end{cases}$$

写成矩阵形式就是

$$\pmatrix{P_x^\prime\\ P_y^\prime} = \pmatrix{\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta}\pmatrix{x\\y}$$

这个二维旋转矩阵很容易拓展到三维空间中绕 $z$ 轴的旋转变换，注意到绕 $z$ 轴的旋转不会改变向量在 $z$ 轴的分量，于是旋转矩阵 $\mathbf {M}_z (\theta)$ 应该表示为

$$\textbf{M}_z(\theta) = \pmatrix{\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1}$$

同理推出绕 $x$ 轴，$y$ 轴旋转的变换矩阵

$$\textbf{M}_x(\theta) = \pmatrix{1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta}, \textbf{M}_y(\theta) = \pmatrix{\cos\theta & 0 & \sin\theta\\ 0 & 1 & 0\\ -\sin\theta & 0 & \cos\theta}$$

最后讨论向量 $\boldsymbol P$ 绕任意轴旋转 $\theta$ 角的表示方法，我们首先给出两个命题（证明略）：

假设旋转轴是一个单位向量 $\boldsymbol A$，则向量 $\boldsymbol P$ 可以分解为分别与向量 $\boldsymbol A$ 平行和垂直的分量 $\text {proj}_\mathbf A \mathbf P = (\mathbf A\cdot\mathbf P)\cdot\mathbf A$ 和 $\text {perp}_\mathbf A \mathbf P = \mathbf P – (\mathbf A\cdot\mathbf P)\cdot\mathbf A$，如下图

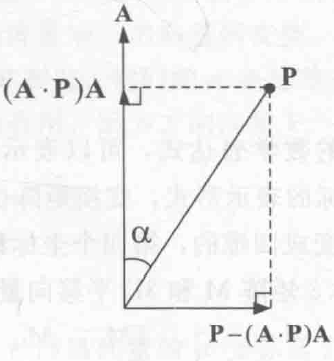
因为向量 $\boldsymbol P$ 绕向量 $\boldsymbol A$ 的旋转可以被分解为 $\text {proj}_\mathbf A \mathbf P$ 和 $\text {perp}_\mathbf A \mathbf P$ 绕向量 $\boldsymbol A$ 的旋转，而 $\text {proj}_\mathbf A \mathbf P$ 显然不变，因此只有 $\text {perp}_\mathbf A \mathbf P$ 发生了旋转。而 $\text {perp}_\mathbf A \mathbf P$ 绕向量 $\boldsymbol A$ 的旋转实际上实在垂直于 $\boldsymbol A$ 的二维平面上进行的，这个二维平面可以用基向量 $(\text {perp}_\mathbf A \mathbf P , \mathbf A\times\mathbf P)$ 表示，因此 $\text {perp}_\mathbf A \mathbf P$ 绕向量 $\boldsymbol A$ 旋转 $\theta$ 角后的向量可以表示为

$$[\mathbf P – (\mathbf A\cdot\mathbf P)\cdot\mathbf A]\cos\theta + (\mathbf A\times \mathbf P)\sin\theta$$

该向量再加上分量 $\text {proj}_\mathbf A \mathbf P$ 就是 $\mathbf P$ 绕向量 $\boldsymbol A$ 旋转 $\theta$ 角后的结果 $\mathbf P^\prime = \mathbf P\cos\theta + (\mathbf A\times \mathbf P)\sin\theta + \mathbf A (\mathbf A\cdot\mathbf P)(1-\cos\theta)$。这就是著名的罗德里格斯旋转公式（Rodrigues’ rotation formula）。

然后，根据上方的两个命题，将 $(\mathbf A\cdot\mathbf P)\cdot\mathbf A$ 和 $\mathbf A\times \mathbf P$ 替换为等效矩阵

$$\mathbf P^\prime = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}\mathbf P\cos\theta + \begin{bmatrix} 0&-A_z&A_y\\ A_z&0&-A_x\\ -A_y&A_x&0 \end{bmatrix}\mathbf P\sin\theta + \begin{bmatrix} A_x^2 & A_xA_y & A_xA_z\\ A_xA_y & A_y^2 & A_yA_z\\ A_xA_z & A_yA_z & A_z^2 \end{bmatrix}\mathbf P(1-\cos\theta)$$

合并上述矩阵，并记 $c=\cos\theta,s=\sin\theta$，则旋转矩阵 $\mathbf M_\mathbf A \theta$ 为

$$\mathbf M_\mathbf A \theta = \begin{bmatrix} c+(1-c)A_x^2 & (1-c)A_xA_y-sA_z & (1-c)A_xA_z+sA_y\\ (1-c)A_xA_y+sA_z & c+(1-c)A_y^2 & (1-c)A_yA_z-sA_x\\ (1-c)A_xA_z-sA_y & (1-c)A_yA_z+sA_x & c+(1-c)A_z^2 \end{bmatrix}$$

拓展到齐次坐标就是 $\pmatrix {\mathbf M_\mathbf A \theta& \bf 0\\ \bf 0 & 1}$。

实际上，描述三维旋转变换最常用的方法是四元数。

四元数

定义

四元数（Quaternions）是复数的一种拓展，定义如下

$$\textbf q = w + xi + yj + zk$$

运算法则

四元数 $\mathbf q$ 通常被写成 $\mathbf q = w + \boldsymbol v = <w, \boldsymbol v>$，其中 $w$ 是标量部分，$\boldsymbol v = xi+yj+zk$ 是向量部分。这里 $i,j,k$ 是复数在四维空间中的拓展，基础计算法则如下

$$\begin{aligned} & i^2=j^2=k^2=ijk=-1\\ & ij=-ji=k\\ & jk=-kj=i\\ & ki=-ik=j\\ \end{aligned}$$

这里 $i,j,k$ 之间的乘法规则定义可以类比叉积、右手法则之类的概念。

两个四元数 $\mathbf q_1 = w_1+x_1i + y_1j + z_1k, \mathbf q_2 = w_2+x_2i + y_2j + z_2k$ 之间的乘法可以表示为

$$\begin{aligned} \textbf q_1\textbf q_2 =& (w_1w_2 – x_1x_2 – y_1y_2 – z_1z_2) +\\ & (w_1x_2 + x_1w_2 + y_1z_2 – z_1y_2)i +\\ & (w_1y_2 – x_1z_2 + y_1w_2 + z_1x_2)j +\\ & (w_1z_2 + x_1y_2 – y_1x_2 + z_1w_2)k \end{aligned}$$

也可以用点乘、叉乘简写为

$$\textbf q_1\textbf q_2 = w_1w_2 – \boldsymbol v_1\cdot\boldsymbol v_2 + s_1\boldsymbol v_2 + s_2\boldsymbol v_1 + \boldsymbol v_1\times\boldsymbol v_2$$

和复数相似地，四元数也有共轭的概念，$\mathbf q= w + xi + yj + zk$ 的共轭为 $\overline {\mathbf q}= w – xi – yj – zk$。可以验证四元数 $\mathbf q$ 和它的共轭 $\overline {\mathbf q}$ 的乘积等于它的内积，即

$$\textbf q\overline{\textbf q} = \textbf q\cdot\textbf q = |\textbf q|^2$$

由此可以求出四元数倒数的计算方法

$$\textbf q^{-1} = \frac{\overline{\textbf q}}{\textbf q^2}$$

四元数旋转

在仿射变换章节中，我们已经推出了向量 $\mathbf P$ 绕单位旋转轴 $\mathbf A$ 旋转 $\theta$ 角的罗德里格斯旋转公式

$$\mathbf P^\prime = \mathbf P\cos\theta + (\mathbf A\times \mathbf P)\sin\theta + \mathbf A(\mathbf A\cdot\mathbf P)(1-\cos\theta)$$

这里向量 $\mathbf P,\mathbf A$ 以及向量 $\mathbf P$ 分解出来的 $\text {proj}_\mathbf A \mathbf P$ 和 $\text {perp}_\mathbf A \mathbf P$ 等向量都可以看作标量为 $0$ 的四元数，记作

$$\begin{aligned} &\textbf p = <0, \textbf P>\\ &\textbf a = <0, \textbf A>\\ &\textbf p_{\parallel} = <0, \text{proj}_\mathbf A \mathbf P>\\ &\textbf p_{\perp} = <0, \text{perp}_\mathbf A \mathbf P>\\ \end{aligned}$$

同时，根据前文的推导已知

$$\begin{aligned} &\text{proj}_\mathbf A \mathbf P = (\mathbf A\cdot\mathbf P)\cdot\mathbf A\\ &\text{perp}_\mathbf A \mathbf P = \mathbf P – (\mathbf A\cdot\mathbf P)\cdot\mathbf A\\ &\text{perp}_\mathbf A \mathbf P^\prime = \text{perp}_\mathbf A \mathbf P\cos\theta + (\mathbf A\times \mathbf P)\sin\theta \end{aligned}$$

记 $\mathbf p_{\perp}^\prime = <0,\text {perp}_\mathbf A \mathbf P^\prime>$，它表示 $\text {perp}_\mathbf A \mathbf P$ 绕轴 $\mathbf A$ 旋转 $\theta$ 角之后的四元数。对于等式 $\text {perp}_\mathbf A \mathbf P^\prime = \text {perp}_\mathbf A \mathbf P\cos\theta + (\mathbf A\times \mathbf P)\sin\theta$，这里 $\text {perp}_\mathbf A\mathbf P^\prime$ 和 $\text {perp}_\mathbf A\mathbf P$ 都可以表示为四元数形式，只剩下一个 $\mathbf A\times \mathbf P$，这个叉积可以利用上方给出的四元数性质（$\mathbf a\mathbf p=<-\mathbf A\cdot \mathbf P,\mathbf A\times \mathbf P>$）进行转化。

因为 $\mathbf P = \text {proj}_\mathbf A \mathbf P + \text {perp}_\mathbf A \mathbf P$，所以 $\mathbf A\times \mathbf P = \mathbf A\times (\text {proj}_\mathbf A \mathbf P + \text {perp}_\mathbf A \mathbf P) = \mathbf A\times \text {perp}_\mathbf A \mathbf P$，于是

$$\mathbf A\times \mathbf P = a\mathbf p_\perp + \mathbf A\cdot\text{perp}_\mathbf A \mathbf P = \mathbf a\mathbf p_\perp$$

综上

$$\mathbf p_\perp^\prime = \mathbf p_\perp\cos\theta + \mathbf a\mathbf p_\perp\sin\theta = (\cos\theta + \mathbf a\sin\theta)\mathbf p_\perp$$

注意到，这里 $\cos\theta + \mathbf a\sin\theta$ 实际上就是一个四元数，记作 $\mathbf q=<\cos\theta,\mathbf a \sin\theta>$。

这个四元数有一个特殊性质

$$\begin{aligned} |\mathbf q| &= \sqrt{\cos^2\theta + (\sin\theta\mathbf a)\cdot (\sin\theta\mathbf a)}\\ &= \sqrt{\cos^2\theta + \mathbf a^2\sin^2\theta}\\ &= \sqrt{\cos^2\theta + \sin^2\theta}\\ &= 1 \end{aligned}$$

最后，我们就能写出罗德里格斯旋转公式（四元数版）：

$$\begin{aligned} \mathbf p^\prime &= \mathbf p_\parallel^\prime + \mathbf p_\perp^\prime\\ &= \mathbf p_\parallel + \mathbf q\mathbf p_\perp \end{aligned}$$

再继续推导之前，我们先证明几个引理：

证明：

$$\begin{aligned} \mathbf q^2 &= <\cos\theta, \mathbf a\sin\theta><\cos\theta, \mathbf a\sin\theta>\\ &= <\cos^2\theta – (\mathbf a\sin\theta) \cdot (\mathbf a\sin\theta), (\cos\theta\sin\theta + \sin\theta\cos\theta)\mathbf a + (\mathbf a\sin\theta) \times (\mathbf a\sin\theta)>\\ &= <\cos^2\theta – \sin^2\theta, 2\mathbf a\cos\theta\sin\theta>\\ &= <\cos 2\theta, \mathbf a \sin 2\theta> \end{aligned}$$

这个引理的几何意义就是绕旋转轴 $\mathbf a$ 旋转 $\theta$ 角两次等价于旋转 $2\theta$ 角一次。有了该引理后，我们对旋转公式进行变形

$$\begin{aligned} \mathbf p^\prime &= \mathbf p_\parallel + \mathbf q\mathbf p_\perp\quad(\mathbf q=<\cos\theta, \mathbf a\sin\theta>)\\ &= 1\cdot \mathbf p_\parallel + \mathbf q\mathbf p_\perp\\ &= \mathbf r\mathbf r^{-1}\mathbf p_\parallel + \mathbf r\mathbf r\mathbf p_\perp\quad(\mathbf r^2 = \mathbf q, \mathbf r=<\cos\frac{\theta}{2}, \mathbf a\sin\frac{\theta}{2}>)\\ \end{aligned}$$

这里我们引入了新的四元数 $\mathbf r$，显然它也是一个单位四元数，满足性质 $\mathbf r^{-1} = \overline {\mathbf r}$，将这个性质代回等式中，则

$$\begin{aligned} \mathbf p^\prime &= \mathbf r\mathbf r^{-1}\mathbf p_\parallel + \mathbf r\mathbf r\mathbf p_\perp\\ &= \mathbf r\overline{\mathbf r} \mathbf p_\parallel + \mathbf r\mathbf r\mathbf p_\perp\\ \end{aligned}$$

先展开等式左边：

$$\begin{aligned} \text{LHS} &= \mathbf q\mathbf p_{\parallel} \\ &= <\alpha, \beta\mathbf a>\cdot<0,\mathbf P_{\parallel}>\\ &= <0-\beta\mathbf a\mathbf P_{\parallel}, \alpha\mathbf P_{\parallel} + 0 + \beta\mathbf a\times \mathbf P_{\parallel}>\\ &= <-\beta\mathbf a\mathbf P_{\parallel}, \alpha\mathbf P_{\parallel}> \end{aligned}$$

再计算等式右边：

$$\begin{aligned} \text{RHS} &= \mathbf p_{\parallel}\mathbf q\\ &= <0,\mathbf P_{\parallel}>\cdot <\alpha, \beta\mathbf a>\\ &= <0 – \beta\mathbf a\mathbf P_{\parallel}, 0 + \alpha\mathbf P_{\parallel} + \mathbf P_\parallel\times\beta\mathbf a>\\ &= <-\beta\mathbf a\mathbf P_\parallel, \alpha\mathbf P_{\parallel}> = \text{LHS} \end{aligned}$$

证明类似于引理 2：

$$\begin{aligned} \text{LHS} &= \mathbf q\mathbf p_\perp\\ &= <\alpha,\beta\mathbf a>\cdot <0,\mathbf P_\perp>\\ &= <0, -\beta\mathbf a\mathbf P_\perp, \alpha\mathbf P_\perp+0+\beta\mathbf a\times\mathbf P_\perp>\\ &= <0, \alpha\mathbf P_\perp+\beta\mathbf a\times\mathbf P_\perp> \end{aligned}$$

$$\begin{aligned} \text{RHS} &= \overline{\mathbf p}_\perp\mathbf q\\ &= <0,\mathbf P_\perp>\cdot<\alpha,-\beta\mathbf a>\\ &= <0+\beta\mathbf a\mathbf P, \alpha\mathbf P_\perp-\mathbf P_\perp\times(-\beta\mathbf a)>\\ &= <0, \alpha\mathbf P_\perp+\beta\mathbf a\times\mathbf P_\perp> = \text{LHS} \end{aligned}$$

于是，我们就能继续对公式 $\mathbf p^\prime =\mathbf r\overline {\mathbf r} \mathbf p_\parallel + \mathbf r\mathbf r\mathbf p_\perp$ 进行变形

$$\begin{aligned} \mathbf p^\prime &= \mathbf r\overline{\mathbf r} \mathbf p_\parallel + \mathbf r\mathbf r\mathbf p_\perp\\ &= \mathbf r\mathbf p_\parallel\overline{\mathbf r} + \mathbf r\mathbf p_\perp\overline{\mathbf r}\\ &= \mathbf r(\mathbf p_\parallel + \mathbf p_\perp)\overline{\mathbf r}\\ &= \mathbf r \mathbf p\overline{\mathbf r}\\ &= \mathbf r \mathbf p{\mathbf r}^{-1}\\ \end{aligned}$$

这就是最终的罗德里格斯旋转公式（四元数化简版），我们将上方所有的推导归纳为一个定理：

此外，四元数的旋转是可以复合的。假设有两个表示沿着不同轴，不同角度旋转的四元数 $\mathbf {q}_1,\mathbf {q}_2$，我们先对某四元数 $\mathbf p = <0,\boldsymbol p>$ 进行 $\mathbf {q}_1$ 变换，得到 $\mathbf {p}^\prime$ 再进行 $\mathbf {q}_2$ 变换，得到 $\mathbf {p}^{\prime\prime}$，这一过程用四元数旋转公式表示就是

$$\begin{aligned} \mathbf p^\prime &= \mathbf{q}_1\mathbf{p}\mathbf{q}_1^{-1}\\ \mathbf p^{\prime\prime} &= \mathbf{q}_2\mathbf{p}^\prime\mathbf{q}_2^{-1} = \mathbf{q}_2\mathbf{q}_1\mathbf{p}\mathbf{q}_1^{-1}\mathbf{q}_2^{-1}\\ \end{aligned}$$

接下来证明，这两个旋转变换可以复合并写成以下形式

$$\mathbf p^{\prime\prime} = \mathbf{q}_{\text{net}} \mathbf p\mathbf{q}_{\text{net}}^{-1}$$

首先给出一个引理：

证明如下

$$\begin{aligned} \text{LHS} &= \overline{\mathbf{q}}_{1}\overline{\mathbf{q}}_{2}\\ &= <s, -\boldsymbol v>\cdot <t,-\boldsymbol u>\\ &= <st -\boldsymbol v\cdot\boldsymbol u, -s\boldsymbol u-t\boldsymbol v + \boldsymbol v\times\boldsymbol u> \end{aligned}$$

$$\begin{aligned} \text{RHS} &= \overline{(\mathbf{q}_{2}\mathbf{q}_{1})}\\ &= (<s, \boldsymbol v>\cdot <t,\boldsymbol u>)^*\\ &= <st-\boldsymbol v\cdot\boldsymbol u, s\boldsymbol u+t\boldsymbol v-\boldsymbol v\times\boldsymbol u>^* = \text{LHS} \end{aligned}$$

上方推导中，$x^*$ 表示求 $x$ 的共轭。于是有

$$\begin{aligned} \mathbf p^{\prime\prime} &= \mathbf{q}_2\mathbf{q}_1\mathbf{p}\mathbf{q}_1^{-1}\mathbf{q}_2^{-1}\\ &= \mathbf{q}_2\mathbf{q}_1\mathbf{p}\overline{\mathbf{q}}_1\overline{\mathbf{q}}_2\\ &= \mathbf{q}_2\mathbf{q}_1\mathbf{p}\overline{\mathbf{q}_2\mathbf{q}_1}\\ &= (\mathbf{q}_2\mathbf{q}_1)\mathbf{p}(\mathbf{q}_2\mathbf{q}_1)^{-1} \end{aligned}$$

也就是说 $\mathbf {q}_{\text {net}} = \mathbf {q}_2\mathbf {q}_1$。这个复合旋转的计算也可以推广到 $n$ 个旋转。

四元数旋转的矩阵形式

注意到，四元数乘法（$\mathbf q_1 = w_1+x_1i + y_1j + z_1k, \mathbf q_2 = w_2+x_2i + y_2j + z_2k$）实际上可以视为一种线性组合

$$\begin{aligned} \textbf q_1\textbf q_2 =& (w_1w_2 – x_1x_2 – y_1y_2 – z_1z_2) +\\ & (w_1x_2 + x_1w_2 + y_1z_2 – z_1y_2)i +\\ & (w_1y_2 – x_1z_2 + y_1w_2 + z_1x_2)j +\\ & (w_1z_2 + x_1y_2 – y_1x_2 + z_1w_2)k\\ =& \begin{bmatrix} w_1 & -x_1 & -y_1 & -z_1\\ x_1 & w_1 & -z_1 & y_1\\ y_1 & z_1 & w_1 & -x_1\\ z_1 & -y_1 & x_1 & w_1 \end{bmatrix} \begin{bmatrix} w_2\\ x_2\\ y_2\\ z_2 \end{bmatrix} \end{aligned}$$

同理有

$$\textbf q_2\textbf q_1 = \begin{bmatrix} w_1 & -x_1 & -y_1 & -z_1\\ x_1 & w_1 & z_1 & -y_1\\ y_1 & -z_1 & w_1 & x_1\\ z_1 & y_1 & -x_1 & w_1 \end{bmatrix} \begin{bmatrix} w_2\\ x_2\\ y_2\\ z_2 \end{bmatrix}$$

利用这个性质将 $\mathbf p^\prime = \mathbf {q}\mathbf {p}\mathbf {q}^{-1}$ 写成矩阵形式，设 $a=\cos\frac {\theta}{2}, b=\sin\frac {\theta}{2} A_x,c=\sin\frac {\theta}{2} A_y,d=\sin\frac {\theta}{2} A_z,\mathbf q = a+bi+cj+dk$，单位旋转轴 $\boldsymbol a=(A_x,A_y,A_z)$，则

$$\begin{aligned} \mathbf q \mathbf p\mathbf q^{-1} &= \mathbf q \mathbf p\overline{\mathbf q}\\ &= \begin{bmatrix} a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{bmatrix} \begin{bmatrix} a & b & c & d\\ -b & a & -d & c\\ -c & d & a & -b\\ -d & -c & b & a \end{bmatrix}\mathbf p \end{aligned}$$

实际上就是四元数 $\mathbf p$ 左乘 $\mathbf q$，右乘 $\overline {\mathbf q}$。利用 $a^2+b^2+c^2+d^2=1$ 的性质，上式可以简化为

$$\begin{aligned} \mathbf q \mathbf p\mathbf q^{-1} &= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1-2c^2-2d^2 & 2bc-2ad & 2ac+2bd\\ 0 & 2bc+2ad & 1-2b^2-2d^2 & 2cd-2ab\\ 0 & 2bd-2ac & 2ab+2cd & 1-2b^2-2c^2 \end{bmatrix} \mathbf p \end{aligned}$$

注意到这个变换矩阵很类似齐次坐标（最外圈不会对 $\mathbf p$ 进行任何变换），因此我们可以将这个矩阵压缩为 $3\times 3$ 矩阵。总结以上推导，我们归纳得到了四元数旋转的矩阵形式

实际上，在上方矩阵形式的三维旋转公式中，已经不再涉及四元数运算了。