分布函数和概率密度函数
分布函数的简单解释:一元情况下,一个连续随机变量 $X$ 的分布函数 $F_X(x)$ 的含义是——$X\le x$ 的概率,因此分布函数有这些性质:
- $\lim_{x\rightarrow -\infty}F_X(x)=0$。
- $\lim_{x\rightarrow +\infty}F_X(x)=1$。
- $F_X(x)$ 右连续且单调不减。
在二元情况下,假设有两个连续随机变量 $X,Y$,他们的分布函数 $F(x,y)$ 表示 $X\le x,Y\le y$ 的概率,即 $P(X\le x\cap Y\le y)$。这也可以推广至 $N$ 维。
概率密度函数(PDF, Probability Density Function)的定义来源于分布函数,一般记 $F_X(x)$ 的密度函数为 $f_X(x)$,定义如下:
$$
F_X(x)=\int_{-\infty}^{x}f_X(x)\mathrm{d}x
$$
根据该定义,可以推出其性质如下:
- $\int_{-\infty}^{+\infty}f_X(x)\mathrm{d}x=1$。
- $f(x)\ge 0$。
二维情况的定义如下:
$$
F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)\mathrm{d}v\mathrm{d}u
$$
同理,可以推广至 $N$ 维。
例题
$$
f(x)=\begin{cases}|x|&-1\lt x\lt 1\\ 0 & \text{otherwise}\end{cases}
$$
令 $Y=X^2+1$,试求:
1. $Y$ 的概率密度 $f_Y(y)$。
2. $P(-1\lt Y\lt\frac{3}{2})$。
子问题1:
首先 $Y=X^2+1$,因此 $f_Y(y)=0,y\le 1$,然后有
$$
P(Y\le y)=P(X^2+1\le y)=P(-\sqrt{y-1}\le X\le\sqrt{y-1})=\int_{-\sqrt{y-1}}^{\sqrt{y-1}}|x|\mathrm{d}x=y-1
$$
因此当 $1\le y\le 2$ 时,$f_Y(y)=y-1$;当 $2\lt y$ 时 $f_Y(y)=0$。
子问题2:
由于 $Y\sim U(1,2)$,因此本题结果为 $P(-1\lt Y\lt\frac{3}{2})=\frac{1}{2}$。
$$
F_Y(y)=P(Y\le y)=P(X^2\le y)=P(-\sqrt{y}\le X\le\sqrt{y})
$$
这里,由于 $X\sim U(0,2)$,因此
$$
F_Y(y)=P(0\le X\le \sqrt{y})=F_X(\sqrt{y})=\frac{\sqrt{y}}{2}
$$
于是概率密度为 $F_X^\prime(\sqrt{y})=\frac{1}{4\sqrt{y}}$。
首先根据题目条件得到
$$
F_X(x)=\begin{cases}1-2e^{-2x} & x\gt 0\\ 0 & x\le 0\end{cases}
$$
然后分类讨论 $y$ 的取值范围,这里只考虑 $0\lt y\lt 1$:
$$
F_Y(y)=P(Y\le y)=P(1-e^{-2X}\le y)=P(X\le-\frac{1}{2}\ln(1-y))=F_X(-\frac{1}{2}\ln(1-y))=y
$$
于是有 $Y\sim U(0,1)$。
常用分布
离散型
伯努利分布(0-1分布)
伯努利分布指的是:单次伯努利试验的分布,假设单次伯努利试验成功概率为 $p$,那么一定有:
$$
P(X=k)=p^k(1-p)^{1-k}\quad(k=0,1,0\lt p\lt 1)
$$
上面的公式就是说明伯努利试验只有两种可能:成功($k$ 取 $1$)的概率是 $p$,反之概率为 $1-p$。
那么,数学期望显然是 $E(X)=p$,方差 $D(X)=E(X-E(X))^2=(1-p)^2p+(0-p)^2(1-p)=p(1-p)$。
二项分布
$n$ 重伯努利试验中,设 $0\lt p\lt 1$ 为事件 $A$ 在一次试验中发生的概率,$X$ 为事件 $A$ 发生的次数,则 $X$ 可能取到值为 $0,1,\cdots,n$,它取这些值的概率为:
$$
P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}
$$
期望和方差:
$$
E(X)=np,\ D(X)=np(1-p)
$$
一个naive的理解是:二项分布就是 $n$ 次伯努利分布的累加,因此期望和方差都是伯努利分布的 $n$ 倍。
泊松分布
泊松分布说的是,当二项分布中 $p\rightarrow 0,n\rightarrow +\infty$ 时,如果它的数学期望是一个常数:$np=\lambda$,那么就有
$$
\begin{aligned}
P(X=k)=\binom{n}{k}p^k(1-p)^{1-k}&= \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}\\
&=\frac{n(n-1)\cdots(n-k+1)}{k!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k}\\
&=\frac{\lambda^k}{k!}(\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-k+1}{n})(1-\frac{\lambda}{n})^{n-k}
\end{aligned}
$$
由于 $n\rightarrow+\infty$,因此 $(1-\frac{\lambda}{n})^{n-k}=e^{-\lambda}$,$\frac{n-k+1}{n}=1$,于是上式的结果 $=\frac{\lambda^k}{k!}e^{-\lambda}$。因此泊松分布的定义就是
$$
P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}
$$
根据泊松分布的定义直接有期望 $E(X)=\lambda$,然后求方差:
$$
D(X)=np(1-p)=\lambda(1-p)=\lambda\quad (p\rightarrow 0)
$$
*泊松分布本质上是二项分布的极限情况。
几何分布
几何分布说的是,进行了 $k$ 次伯努利实验,并且只有最后一次实验成功的概率:
$$
P(X=k)=p(1-p)^{k-1}
$$
期望和方差:
$$
E(X)=\frac{1}{p},\ D(X)=\frac{1-p}{p^2}
$$
期望的证明非常简单,这里证明方差:
$$
D(X)=E(X^2)-E(X)^2=E(X)-\frac{1}{p}^2=\frac{1-p}{p^2}\quad(几何分布中E(X^2)就是E(X))
$$
连续型
均匀分布
设随机变量 $X\sim U(a,b)$,则 $X$ 的概率密度为
$$
f(x)=\begin{cases}
\frac{1}{b-a}&a\lt x\lt b\\
0&\text{otherwise}
\end{cases}
$$
显然有期望 $E(X)=\frac{a+b}{2}$,方差为:
$$
\begin{aligned}
D(X)&=E(X^2)-E(X)^2\\
&=\int_a^bx^2\frac{1}{b-a}\mathrm{d}x-\bigg(\frac{a+b}{2}\bigg)^2\\
&=\frac{(b-a)^2}{12}
\end{aligned}
$$
指数分布
设随机变量 $X$ 服从指数分布,其概率密度为
$$
f(x)=\begin{cases}
\lambda e^{-\lambda x}& x\gt 0\\
0 & x\le 0
\end{cases}\quad \lambda\gt 0
$$
记作 $X\sim E(\lambda)$,积分后即可得到分布函数:
$$
F(x)=\begin{cases}
1- e^{-\lambda x} & x\gt 0\\
0 & x\le 0
\end{cases}
$$
期望:
$$
\begin{aligned}
E(X)=\int_{-\infty}^{+\infty} xf(x)\mathrm{d}x&=\int_{0}^{+\infty}\lambda xe^{-\lambda x}\mathrm{d}x\\
&=\frac{1}{\lambda}
\end{aligned}
$$
方差:
$$
\begin{aligned}
D(X)=E(X^2)-E(X)^2&=\int_{-\infty}^{+\infty}x^2f(x)\mathrm{d}x-\frac{1}{\lambda}^2\\
&=\int_{0}^{+\infty}x^2\mathrm{d}(-\frac{1}{\lambda}e^{-\lambda x})-\frac{1}{\lambda}^2\\
&=-\frac{1}{\lambda}e^{-\lambda x}x^2\bigg|_0^{+\infty}-2\int{0}^{+\infty}-\frac{1}{\lambda}xe^{-\lambda x}\mathrm{d}x-\frac{1}{\lambda}^2\\
&=\frac{1}{\lambda}^2
\end{aligned}
$$
正态分布
正态分布的概率密度:
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\ -\infty\lt x\lt +\infty
$$
其中 $\mu,\sigma(\sigma\gt 0)$ 是常数,记作 $X\sim N(\mu,\sigma^2)$。
期望和方差
正态分布的期望和方差就是概率密度函数的两个参数
$$
E(X)=\mu,\ D(X)=\sigma^2
$$
标准化
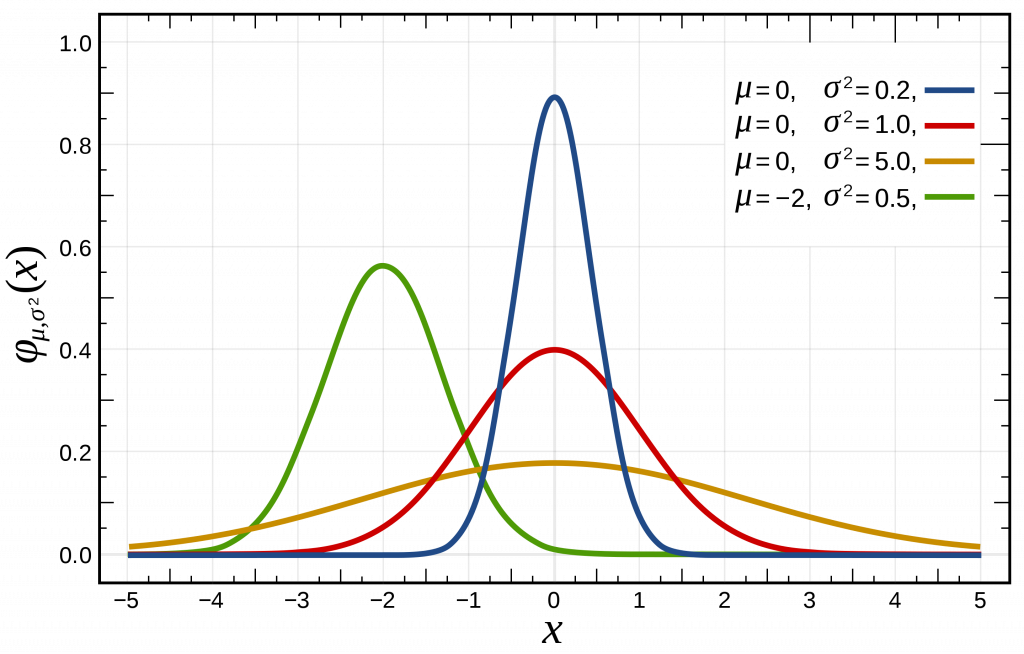
如图,上方红色曲线即标准正态分布的概率密度函数:$N(0,1^2)$。
任意一个正态分布 $X\sim N(\mu,\sigma^2)$ 都可以通过线性变换转化为标准正态分布,方法如下:
$$
Z=\frac{X-\mu}{\sigma}
$$
则 $Z\sim N(0,1^2)$。
性质
- 正态分布 $N(\mu,\sigma^2)$ 的概率密度函数是一个轴对称图像,关于 $x=\mu$ 对称。
- 独立的正态分布具有可加性:若 $X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$,且 $X,Y$ 相互独立,则 $X+Y\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$;$X-Y\sim N(\mu_1-\mu_2,\sigma_1^2+\sigma_2^2)$。
例题
$$
P(1\lt X\lt 2)\Leftrightarrow P(1^3\lt X^3\lt 2^3)
$$
记 $Z=\frac{X^3-1}{7}$(将 $X^3$ 标准化),则 $Z\sim N(0,1)$,此时显然有:
$$
P(1^3\lt X^3\lt 2^3)\Leftrightarrow P(0\lt Z\lt 1) = \Phi(1)-\Phi(0)=\Phi(1)-0.5
$$
多维随机变量
二维离散型随机变量
例题
设随机变量 $X_i$ 服从分布
| $X_i$ | $-1$ | $0$ | $1$ |
|---|---|---|---|
| $P$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
$i=1,2$,且 $P(X_1X_2=0)=1$,则 $P(X_1=X_2)=$?
题设条件实际上给出了二维离散型随机变量 $(X_1,X_2)$ 的边缘分布,我们需要由此求出联合分布:
| $X_1\backslash X_2$ | $-1$ | $0$ | $1$ | $p_i$ |
|---|---|---|---|---|
| $-1$ | $\frac{1}{4}$ | |||
| $0$ | $\frac{1}{2}$ | |||
| $1$ | $\frac{1}{4}$ | |||
| $p_j$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
此外,根据条件 $P(X_1X_2=0)=1$ 可知 $X_1,X_2$ 中至少有一个元素为 $0$,因此 $P(X_1\neq0,X_2\neq0)=0$,即:
| $X_1\backslash X_2$ | $-1$ | $0$ | $1$ | $p_i$ |
|---|---|---|---|---|
| $-1$ | $0$ | $0$ | $\frac{1}{4}$ | |
| $0$ | $\frac{1}{2}$ | |||
| $1$ | $0$ | $0$ | $\frac{1}{4}$ | |
| $p_j$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
此时根据边缘密度的定义即可推出完整的联合分布:
| $X_1\backslash X_2$ | $-1$ | $0$ | $1$ | $p_i$ |
|---|---|---|---|---|
| $-1$ | $0$ | $\frac{1}{4}$ | $0$ | $\frac{1}{4}$ |
| $0$ | $\frac{1}{4}$ | $0$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| $1$ | $0$ | $\frac{1}{4}$ | $0$ | $\frac{1}{4}$ |
| $p_j$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
因此本题答案为 $0$。
设随机变量 $X,Y$ 相互独立,填满下表:
| $X\backslash Y$ | $y_1$ | $y_2$ | $y_3$ | $p_i$ |
|---|---|---|---|---|
| $x_1$ | $\frac{1}{8}$ | |||
| $x_2$ | $\frac{1}{8}$ | |||
| $p_j$ | $\frac{1}{6}$ |
注意本题条件 $X,Y$ 相互独立,因此 $p_{ij}=p_ip_j$(也就是说,如果 $p_{ij},p_i,p_j$ 三个中至少知道两个就可以算出另一个的值),此外根据边缘分布的性质(同一边缘密度之和等于 $1$)即有:
| $X\backslash Y$ | $y_1$ | $y_2$ | $y_3$ | $p_i$ |
|---|---|---|---|---|
| $x_1$ | $\frac{1}{24}$ | $\frac{1}{8}$ | $\frac{1}{12}$ | $\frac{1}{4}$ |
| $x_2$ | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{1}{4}$ | $\frac{3}{4}$ |
| $p_j$ | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{1}{3}$ |
二维连续型随机变量
设 $F(x,y)$ 是二维随机变量 $(X,Y)$ 的联合分布函数,如果存在非负函数 $f(x,y)$,使得对任意实数 $x,y$ 有:
$$
F(x,y)=\int_{-\infty}^y\int_{-\infty}^{x}f(u,v)\mathrm{d}u\mathrm{d}v
$$
称 $(X,Y)$ 是二维连续型随机变量,称 $f(x,y)$ 是 $(X,Y)$ 的联合概率密度函数。$F(x,y)$ 的实际意义是 $P(X\le x,Y\le y)$。
二维连续型随机变量的边缘分布
边缘分布函数定义如下:
$$
F_X(x)=F(x,+\infty)=\int_{-\infty}^x\int_{-\infty}^{+\infty}f(u,v)\mathrm{d}u\mathrm{d}v=\int_{-\infty}^x\bigg[\int_{-\infty}^{+\infty}f(u,v)\mathrm{d}v\bigg]\mathrm{d}u
$$
边缘密度函数定义如下:
$$
f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}y
$$
因此:
$$
F_X(x)=\int_{-\infty}^xf_X(u)\mathrm{d}u
$$
二维连续型随机变量的条件分布
称 $F_{X|Y}(x|y)$ 为在条件 $Y=y$ 下 $X$ 的条件分布函数。
$$
F_{X|Y}(x|y)=P{X\le x|Y=y}=\int_{-\infty}^x\frac{f(u,y)}{f_Y(y)}\mathrm{d}u
$$
称 $f_{X|Y}(x|y)$ 为在条件 $Y=y$ 下 $X$ 的条件密度函数。
$$
f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}
$$
二维连续型随机变量的相互独立性
随机变量 $(X,Y)$ 相互独立的充要条件为 $F(x,y)=F_X(x)F_Y(y)$。当 $(X,Y)$ 是连续型随机变量时,等价于 $f(x,y)=f_X(x)f_Y(y)$。
当 $(X,Y)$ 相互独立时,有
$$
f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}=\frac{f_X(x)f_Y(y)}{f_Y(y)}=f_X(x)
$$
特殊二维连续型随机变量的分布
Z=X+Y
设 $(X,Y)$ 是二维连续型随机变量,其联合密度函数为 $f(x,y)$,则 $Z=X+Y$ 的分布函数如下:
$$
\begin{aligned}
F_Z(z)=P(Z\le z)&=P(X+Y\le z)\\
&=\iint_{x+y\le z} f(x,y)\mathrm{d}x\mathrm{d}y\\
&=\int_{-\infty}^{+\infty}\bigg[\int_{-\infty}^{z-x}f(x,y)\mathrm{d}y\bigg]\mathrm{d}x\\
&\overset{x+y=u}{=\!=\!=\!=} \int_{-\infty}^{+\infty}\bigg[ \int_{-\infty}^{z}f(x,u-x)\mathrm{d}u \bigg]\mathrm{d}x\\
&=\int_{-\infty}^z \bigg[\int_{-\infty}^{+\infty}f(x,u-x)\mathrm{d}x\bigg]\mathrm{d}u
\end{aligned}
$$
则 $Z$ 的密度函数如下:
$$
f_Z(z)=\frac{\mathrm{d}F_z(Z)}{\mathrm{d}z}=\int_{-\infty}^{+\infty}f(x,z-x)\mathrm{d}x
$$
同理,有 $y$ 的对称形式:
$$
f_Z(z)=\int_{-\infty}^{+\infty}f(z-y,y)\mathrm{d}y
$$
特别地,当 $X,Y$ 相互独立时:
$$
f_Z(z)=\int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)\mathrm{d}x=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)\mathrm{d}y
$$
Z=X/Y, Z=XY
设 $(X,Y)$ 是二维连续型随机变量,它具有概率密度 $f(x,y)$,则 $Z=\frac{Y}{X},XY$ 仍为随机变量,其概率密度分别为:
$$
\begin{aligned}
f_{Y/X}(z)&=\int_{-\infty}^{+\infty}|x|f(x,xz)\mathrm{d}x\\
f_{XY}(z)&=\int_{-\infty}^{+\infty}\frac{1}{|x|}f(x,\frac{z}{x})\mathrm{d}x
\end{aligned}
$$
若 $X,Y$ 相互独立则:
$$
\begin{aligned}
f_{Y/X}(z)&=\int_{-\infty}^{+\infty}|x|f_X(x)f_Y(xz)\mathrm{d}x\\
f_{XY}(z)&=\int_{-\infty}^{+\infty}\frac{1}{|x|}f_X(x)f_Y(\frac{z}{x})\mathrm{d}x
\end{aligned}
$$
证明:
$$
\begin{aligned}
F_{Y/X}(z)=P(Y/X\le z)&=\iint_{y/x\le z}f(x,y)\mathrm{d}x\mathrm{d}y\\
&=\iint_{y/x\le z,x\lt 0}f(x,y)\mathrm{d}x\mathrm{d}y+\iint_{y/x\le z,x\gt 0}f(x,y)\mathrm{d}x\mathrm{d}y\\
&=\int_{-\infty}^0\bigg[\int_{zx}^{+\infty}f(x,y)\mathrm{d}y\bigg]\mathrm{d}x+\int_{0}^{+\infty}\bigg[\int_{-\infty}^{zx}f(x,y)\mathrm{d}y\bigg]\mathrm{d}x\\
&\overset{y=xu}{=\!=\!=\!=}\int_{-\infty}^0\bigg[\int_{-\infty}^zf(x,xu)\mathrm{d}(xu)\bigg]\mathrm{d}x+\int_{0}^{+\infty}\bigg[\int_{-\infty}^zf(x,xu)\mathrm{d}(xu)\bigg]\mathrm{d}x\\
&=\int_{-\infty}^{+\infty}\int_{-\infty}^z|x|f(x,xu)\mathrm{d}u\mathrm{d}x\\
&=\int_{-\infty}^z\int_{-\infty}^{+\infty}|x|f(x,xu)\mathrm{d}x\mathrm{d}u\\
&\Rightarrow f_{Y/X}(z)=\int_{-\infty}^{+\infty}|x|f(x,xz)\mathrm{d}x
\end{aligned}
$$
M=max{X,Y}, N=min{X,Y}
设 $X,Y$ 是两个相互独立的随机变量,它们的分布函数分别为 $F_X(x),F_Y(y)$,则
$$
F_M=P(M\le z)=P(X\le z,Y\le z)
$$
由于 $X,Y$ 相互独立,得到
$$
F_\max(z)=P(X\le z)P(Y\le z)=F_X(z)F_Y(z)
$$
类似地有
$$
F_\min(z)=P(N\le z)=1-P(N\gt z)=1-P(X\gt z,Y\gt z)=1-[1-F_X(z)][1-F_Y(z)]
$$
二维正态分布
设有二维连续型随机向量 $X$ 服从二维正态分布,其联合概率密度函数如下:
$$
f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\bigg\{ \frac{-1}{2(1-\rho^2)} \bigg[ \frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} +\frac{(y-\mu_2)^2}{\sigma_2^2}\bigg]\bigg\}
$$
其中 $\mu_1,\mu_2\in R;\sigma_1,\sigma_2\gt 0;-1\lt\rho\lt 1$,记作 $X\sim N(\mu_1,\mu_2;\sigma_1,\sigma_2;\rho)$。图像如下:
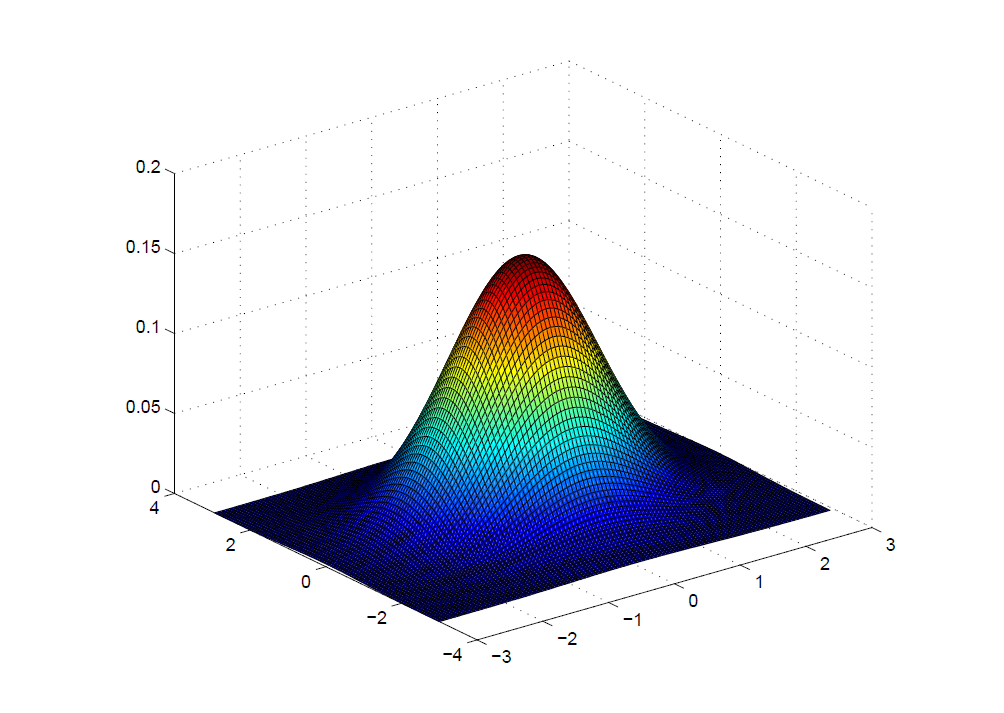
*正常而言,定义式对于做题基本没用。
性质
- 当 $\rho=0$ 时,$X,Y$ 相互独立。
- 边缘密度就是一维正态分布的概率密度($X\sim N(\mu_1,\sigma^2_1),Y\sim N(\mu_2,\sigma_2^2)$):
$$
\begin{aligned}
f_X(x)&=\int_{-\infty}^{+\infty} f(x,y)\mathrm{d}y=\frac{1}{\sqrt{2\pi\sigma_1}}\exp\bigg[-\frac{(x-\mu_1)^2}{2\sigma_1^2}\bigg]\\
f_Y(y)&=\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}x=\frac{1}{\sqrt{2\pi\sigma_2}}\exp\bigg[-\frac{(y-\mu_2)^2}{2\sigma_2^2}\bigg]
\end{aligned}
$$ - 条件分布:
$$
X|Y\sim N\bigg(\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\bigg),Y|X\sim N\bigg(\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1),\sigma_2^2(1-\rho^2)\bigg)
$$
例题
设二维随机变量 $(X,Y)$ 的概率密度为
$$
f(x,y)=\begin{cases}e^{-y}&0\lt x\lt y\\ 0 & \text{otherwise}\end{cases}
$$
- 求 $f_X(x),f_Y(y)$,并判断 $X,Y$ 是否独立。
- 求 $f_{X|Y}(x|y),f_{Y|X}(y|x)$。
子问题1:
以 $f_X(x)$ 为例
$$
f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}y
$$
这里注意分类讨论,若 $x\le 0$,则 $f_X(x)=0$;若 $x\gt 0$ 则
$$
f_X(x)=\int_{x}^{+\infty}e^{-y}\mathrm{d}y=-e^{-y}\bigg|_{x}^{+\infty}=e^{-x}
$$
对于 $f_Y(y)$ 同理:
$$
f_Y(y)=\begin{cases} \int{-\infty}^{+\infty}f(x,y)\mathrm{d}x=\int_{0}^ye^{-y}\mathrm{d}x=ye^{-y} & y\gt 0\\
0 & \text{otherwise}
\end{cases}
$$
子问题2:
先求 $f_{X|Y}(x|y)$,根据公式 $f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$ 有:
$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}=\begin{cases}
\frac{1}{y} & 0\lt x\lt y\\
0 & \text{otherwise}
\end{cases}$$
再求 $f_{Y|X}(y|x)$:
$$
f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}=\begin{cases}
e^{x-y} & 0\lt x\lt y\\
0 & \text{otherwise}
\end{cases}
$$
设 $X\sim U(0,1)$,在 $X=x$ 的条件下,$Y\sim U(0,x)$,求:
- 随机变量 $X,Y$ 的联合概率密度。
- $Y$ 的概率密度。
- $P(X+Y\gt 1)$。
子问题1:
题设条件转化成概率论的语言就是:
$$
f_{X}(x)=\begin{cases}1 & 0\lt x\lt 1\\ 0 & \text{otherwise}\end{cases},\
f_{Y|X}(y|x)=\begin{cases}
\frac{1}{x} & 0\lt y\lt x\lt 1\\
0&\text{otherwise}
\end{cases}
$$
然后根据条件概率的定义有:
$$
f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}\Rightarrow f(x,y)=\begin{cases}
\frac{1}{x} & 0\lt y\lt x\lt 1\\
0 & \text{otherwise}
\end{cases}
$$
这里出于严谨性,实际上还需要验证一下上方的概率密度积分和为 $1$,满足概率密度的定义。
子问题2:
这类题的难度在于搞清楚积分的区间,本例中由于求的是 $Y$ 的边缘密度,因此是对 $x$ 从左往右积分,积分区间是 $[y,1]$。
$$
f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}x=\begin{cases}
\int_{y}^1\frac{1}{x}\mathrm{d}x=-\ln y & 0\lt y\lt 1\\
0 & \text{otherwise}
\end{cases}
$$
子问题3:
本题也是只需要搞清楚积分区间即可,下方蓝色区域即所求积分区域:
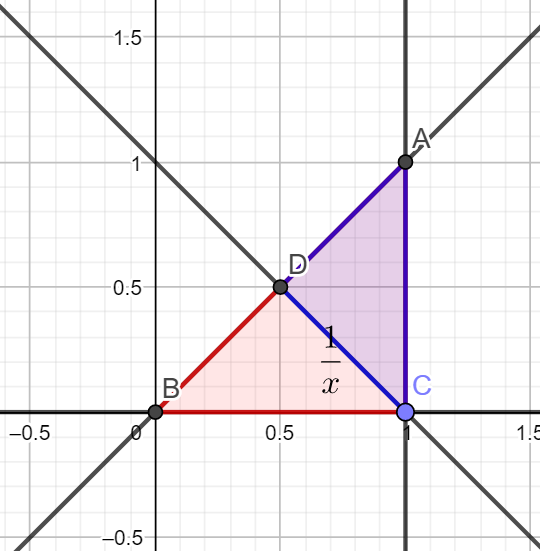
$$
P(X+Y\gt 1)=\int_{0.5}^{1}\int_{1-x}^{x}\frac{1}{x}\mathrm{d}y\mathrm{d}x=1-\ln 2
$$
设二维随机变量 $(X,Y)$ 的概率密度为
$$
f(x,y)=\begin{cases}
1 & 0\lt x\lt 1,0\lt y\lt 2x\\
0 & \text{otherwise}
\end{cases}
$$
- 求 $f_X(x),f_Y(y)$。
- $Z=2X-Y$ 的概率密度 $f_Z(z)$。
- $P(Y\le\frac{1}{2} | X\le \frac{1}{2})$。
子问题1:
分类讨论,当 $0\le x\le 1$ 时:
$$
\begin{aligned}
f_X(x) &= \int_{-\infty}^{+\infty}f(x,y)\mathrm{d}y\\
&=\int_0^{2x}1\mathrm{d}y\\
&=2x
\end{aligned}
$$
其他情况显然有 $f_X(x)=0$。
$$
f_Y(y)=\begin{cases}
1-\frac{y}{2} & 0\lt y\lt 2\\
0 & \text{otherwise}
\end{cases}
$$
子问题2:
$$
\begin{aligned}
F_Z(z)=P(Z\le z)=P(2X-Y\le z) &= \iint_{2x-y\le z}f(x,y)\mathrm{d}x\mathrm{d}y
\end{aligned}
$$
求该二重积分需要对 $z$ 的取值范围分类讨论:
- $z\le 0$,显然 $F_Z(z)=0$。
- $z\ge 2$,显然 $F_Z(z)=1$。
- $0\lt z\lt 2$:
$$
\begin{aligned}
\iint_{2x-y\le z}f(x,y)\mathrm{d}x\mathrm{d}y &= 1-\int_{\frac{z}{2}}^1\int_0^{2x-z}1\mathrm{d}y\mathrm{d}x\\
&=-\frac{z^2}{4}+z
\end{aligned}
$$
最后根据分布求出概率密度:
$$
f_Z(z)=
\begin{cases}
0 & z\le 0\\
1-\frac{z}{2} & 0\lt z\lt 2\\
0 & z\ge 2\\
\end{cases}
$$
子问题3:
画图可知答案是 $\frac{3}{4}$。
设随机变量 $X,Y$ 相互独立,$X$ 的概率分布为 $P(X=i)=\frac{1}{3}(i=-1,0,1)$,$Y$ 的概率密度为
$$
f_Y(y)=\begin{cases}1&0\le y\lt 1\\ 0 & \text{otherwise}\end{cases}
$$
记 $Z=X+Y$。
- 求 $P(Z\le\frac{1}{2} | X=0)$。
- 求 $Z$ 的概率密度 $f_Z(z)$。
子问题1:
$$
\begin{aligned}
P(Z\le\frac{1}{2}|X=0)&=\frac{P(Z\le \frac{1}{2},X=0)}{P(X=0)}\\
&=3\cdot P(Y\le\frac{1}{2},X=0)\\
&=\frac{1}{2}
\end{aligned}
$$
子问题2:
由于 $Z$ 是一个复合的随机变量(既有离散变量又有连续变量),因此我们枚举离散随机变量 $X$。
$$
\begin{aligned}
F_Z(z)=P(Z\le z)&=P(X+Y\le z)\\
&=P(X=-1,-1+Y\le z) + P(X=0,Y\le z) + P(X=1,1+Y\le z)\\
&=\begin{cases}
\frac{1}{3}y+\frac{1}{3} & -1\le z\le 2\\
0 & \text{otherwise}
\end{cases}
\end{aligned}
$$
因此
$$
f_Z(z)=\begin{cases}
\frac{1}{3} & -1\le z \le 2\\
0 & z\le -1\\
1 & \text{otherwise}
\end{cases}
$$
设随机变量 $X,Y$ 相互独立,且 $X\sim N(0,1)$,$Y$ 的概率分布为 $P(Y=0)=P(Y=1)=\frac{1}{2}$,记 $F_Z(z)$ 为随机变量 $Z=XY$ 的分布函数,求 $F_Z(z)$。
$$
\begin{aligned}
F_Z(z)=P(XY\le z)&=P(Y=0,0\le z) + P(Y=1,X\le z)\\
&=\begin{cases}\frac{1}{2} & 0\le z\ 0 & z\lt 0\end{cases} + \frac{1}{2}\Phi(z)\\
&=\begin{cases}\frac{1}{2}(1+\Phi(z)) & 0\le z\ \frac{1}{2}\Phi(z) & z\lt 0\end{cases}
\end{aligned}
$$
设二维随机变量 $(X,Y)$ 的概率密度为 $f(x,y)=Ae^{-2x^2+2xy-y^2},-\infty\lt x,y\lt +\infty$,求常数 $A$ 及条件概率密度 $f_{Y|X}(y|x)$。
求常数 $A$ 显然就是根据概率密度的定义:
$$
\begin{aligned}
\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}Ae^{-2x^2+2xy-y^2}\mathrm{d}x\mathrm{d}y&=1\\
\frac{1}{\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-2x^2+2xy-y^2}\mathrm{d}x\mathrm{d}y}&=A
\end{aligned}
$$
因此只需要求 $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-2x^2+2xy-y^2}\mathrm{d}x\mathrm{d}y$:
$$
\begin{aligned}
\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-2x^2+2xy-y^2}\mathrm{d}x\mathrm{d}y&=\int_{-\infty}^{+\infty}e^{-x^2}\int_{-\infty}^{+\infty}e^{-(y-x)^2}\mathrm{d}y\mathrm{d}x\\
&\overset{y-x=z}{=\!=\!=\!=}\int_{-\infty}^{+\infty}e^{-x^2}\int_{-\infty}^{+\infty}e^{-z^2}\mathrm{d}z\mathrm{d}x\\
&=\pi
\end{aligned}
$$
于是 $A=\frac{1}{\pi}$。
$$
f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}=\frac{\pi e^{-2x^2+2xy-y^2}}{\int_{-\infty}^{+\infty}\pi e^{-2x^2+2xy-y^2}\mathrm{d}y}=\frac{\pi e^{-2x^2+2xy-y^2}}{\pi\sqrt\pi e^{-x^2}}=\frac{e^{-x^2+2xy-y^2}}{\sqrt\pi}
$$
设二维随机变量 $(X,Y)$ 服从区域 $G$ 上的均匀分布,其中 $G$ 是由 $x-y=0,x+y=2,y=0$ 围成的三角形区域。
- 求 $X$ 的概率密度 $f_X(x)$。
- 求条件概率密度 $f_{X|Y}(x|y)$。
子问题1:
由于是均匀分布,画图后即可求出:
$$
f_X(x)=\begin{cases}
x & 0\le x\le 1\\
2-x & 1\le x\le 2\\
0 & \text{otherwise}
\end{cases}
$$
子问题2:
$$
f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}
$$
先求 $f_Y(y)$:
$$
f_Y(y)=\begin{cases}
2(1-y)&0\le y\le 1\\
0&\text{otherwise}
\end{cases}
$$
于是当 $Y=y\in[0,1]$ 时:
$$
f_{X|Y}(x|y)=\begin{cases}
\frac{1}{2(1-y)} & y\le x\le 2-y\\
0 & \text{otherwise}
\end{cases}
$$
上文中给出过 $Z=X+Y$ 型随机变量的一系列结论,因此这里省略一些推导过程:
$$
\begin{aligned}
f_Z(z)=\frac{\mathrm{d}F_z(Z)}{\mathrm{d}z}&=\int_{-\infty}^{+\infty}f(x,z-x)\mathrm{d}x\\
&=\int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)\mathrm{d}x\quad (X,Y独立)\\
&=\int_{z-1}^{z+1} \frac{1}{2}\varphi(x)\mathrm{d}x\quad (-1\le z-x\le 1)\\
&=\Phi(z+1)-\Phi(z-1)
\end{aligned}
$$
$$
F_\max(z)=P(X\le z)P(Y\le z)=F_X(z)F_Y(z)
$$
注意,这里说明了 $X,Y$ 独立且同分布,因此
$$
F_X(z)F_Y(z)=F^2(z)\Leftrightarrow F^2(x)
$$
本题易错点:容易写成 $F(x)F(y)$。
利用容斥原理:
$$
\begin{aligned}
P(1\le\min(X,Y)\le 2) &= P(\min(X,Y)\le 2)-P(\min(X,Y)\le 1)\\
&=P(X\le 2\cup Y\le 2)-P(X\le 1\cup Y\le 1)\\
&=P(X\le 2)^2-P(X\le 1)^2\\
&=e^{-2}-e^{-4}
\end{aligned}
$$
看到 $(X,Y)\sim \Phi(2x)\Phi(y-1)$,容易联想到这就是二维正态分布。当 $\rho=0$ 时,二维正态分布中 $X,Y$ 相互独立,因此 $X$ 对应 $\Phi(2x)$,$Y$ 对应 $\Phi(y-1)$。
$$
\begin{aligned}
F_X(x)=P(X\le x)&=\Phi(2x)\\
P(\frac{X-\mu}{\sigma}\le\frac{x-\mu}{\sigma})&=\Phi(2x)\\
\frac{x-\mu}{\sigma}&=2x\\
\end{aligned}
$$
于是有 $\mu=0,\sigma=\frac{1}{2}$,即 $X\sim N(0,\frac{1}{2}^2)$。同理求出 $Y$:
$$
\begin{aligned}
F_Y(y)=P(Y\le y)&=\Phi(y-1)\\
P(\frac{Y-\mu}{\sigma}\le\frac{y-\mu}{\sigma})&=\Phi(y-1)\\
\frac{y-\mu}{\sigma}=y-1
\end{aligned}
$$
从而 $Y\sim N(1,1^2)$。因此 $(X,Y)\sim N(0,1;\frac{1}{4},1;0)$。
这个做法时不严谨的,实际上第一步应该先验证 $X,Y$ 相互独立,才能求出 $\rho=0$:
$$
F_X(x)=F(x,+\infty)=\Phi(2x),F_Y(y)=F(+\infty,y)=\Phi(y-1)\Rightarrow F_X(x)F_Y(y)=F(x,y)
$$
数学期望和方差
离散型随机变量
期望
设离散型随机变量 $X$ 的概率分布为
$$
P(X=x_k)=p_k\quad k=1,2,\cdots
$$
如果级数 $\sum_{k-1}^{\infty}x_kp_k$ 绝对收敛,则称此级数为随机变量 $X$ 的数学期望,即
$$
E(X)=\sum_{k=1}^\infty x_kp_k
$$
性质
- 期望的线性性质:$E(aX+bY)=aE(X)+bE(Y)$。
- 当且仅当 $X,Y$ 不相关时,$E(XY)=E(X)E(Y)$。
方差
离散型随机变量 $X$ 的方差是数学期望 $E{[X-E(X)]^2}$:
$$
D(X)=E{[X-E(X)]^2}
$$
性质
- $D(X)=E(X^2)-E(X)^2$。
$$
\begin{aligned}
D(X)&=E{[X-E(X)]^2}\\
&=E{X^2-2XE(X)+E(X)^2}\\
&=E(X^2)-2E(X)^2+E(X)^2\quad(E(X)是常数)\\
&=E(X^2)-E(X)^2
\end{aligned}
$$ - $D(aX+b)=a^2D(X)$。
- 当且仅当 $X,Y$ 不相关时,$D(X\pm Y)=D(X)+D(Y)$。
连续型随机变量
*上方离散型随机变量的性质对于连续型也成立。
期望
设连续型随机变量 $X$ 的概率密度为 $f(x)$,若积分
$$
\int_{-\infty}^{+\infty} xf(x)\mathrm{d}x
$$
绝对收敛,则称积分 $\int_{-\infty}^{+\infty} xf(x)\mathrm{d}x$ 的值为随机变量 $X$ 的数学期望。
方差
连续型随机变量 $X$ 的方差仍然是数学期望 $E{[X-E(X)]^2}$,我们利用性质 $D(X)=E(X^2)-E(X)^2$ 计算:
$$
D(X)=\int_{-\infty}^{+\infty}x^2f(x)\mathrm{d}x-\bigg[\int_{-\infty}^{+\infty} xf(x)\mathrm{d}x\bigg]^2
$$
期望的一些拓展
随机变量 $X$ 的函数 $Y=g(X)$ 的期望
- 设 $X$ 的概率分布为
$$
P(X=x_k)=p_k\quad k=1,2,\cdots
$$
如果级数 $\sum_{k=1}^\infty g(x_k)p_k$ 绝对收敛,则 $Y=g(X)$ 的数学期望为
$$
E(Y)=E[g(X)]=\sum_{k=1}^\infty g(x_k)p_k
$$ - 设 $X$ 的概率密度为 $f(x)$,如果积分 $\int_{-\infty}^{+\infty}g(x)f(x)\mathrm{d}x$ 绝对收敛,则 $Y=g(X)$ 的数学期望为
$$
E(Y)=E[g(X)]=\int_{-\infty}^{+\infty}g(x)f(x)\mathrm{d}x
$$
随机变量 $(X,Y)$ 的函数 $Z=g(X,Y)$ 的期望
- 设随机变量 $(X,Y)$ 的概率分布为
$$
P(X=x_i,Y=y_j)=p_{ij}\quad i,j=1,2,\cdots
$$
如果级数 $\sum_{i=1}^\infty\sum_{j=1}^\infty g(x_i,y_j)p_{ij}$ 绝对收敛,则 $Z=g(X,Y)$ 的期望为
$$
E(Z)=E[g(X,Y)]=\sum_{i=1}^\infty\sum_{j=1}^\infty g(x_i,y_j)p_{ij}
$$ - 设 $(X,Y)$ 的概率密度为 $f(x,y)$,如果积分 $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)\mathrm{d}x\mathrm{d}y$ 绝对收敛,则随机变量 $Z=g(X,Y)$ 的期望为
$$
E(Z)=E[g(X,Y)]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)\mathrm{d}x\mathrm{d}{y}
$$
*其实就是期望的定义:概率的加权平均值,这里的权重变成了一个函数 $g$。
例题
$$
f(x)=
\begin{cases}
\frac{1}{\theta}e^{-x/\theta}&x\gt 0\\
0&x\le 0
\end{cases}
\quad\theta\gt 0
$$
若将这两个电子装置串联组成整机,求整机寿命 $N$ 的数学期望。
根据 $X_k$ 的密度函数可以求出其分布:
$$
F(x)=
\begin{cases}
1-e^{-x/\theta} & x\gt 0\\
0 & x\le 0
\end{cases}
$$
由于两个电子装置串联,因此 $N=\min{X_1,X_2}$ 的分布为:
$$
F_\min(x)=1-[1-F(x)]^2=
\begin{cases}
1-e^{-2x/\theta}&x\gt 0\\
0&x\le 0
\end{cases}
$$
于是 $f_\min$ 的概率密度为:
$$
f_\min(x)=
\begin{cases}
\frac{2}{\theta}e^{-2x/\theta}&x\gt 0\\
0&x\le 0
\end{cases}
$$
数学期望为:
$$
E(N)=\int_{0}^{+\infty}x\cdot\frac{2}{\theta}e^{-2x/\theta}\mathrm{d}x=\frac{\theta}{2}
$$
根据分布函数,容易求出密度函数为 $f(x)=\frac{1}{2}\varphi(x)+\frac{1}{4}\varphi(\frac{x-4}{2})$,$\varphi(x)=\Phi(x)^\prime=\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})$。于是
$$
\begin{aligned}
E(X)&=\frac{1}{2\sqrt{2\pi}}\int_{-\infty}^{+\infty}xe^{-\frac{x^2}{2}}+\frac{1}{2}xe^{-\frac{(\frac{x-4}{2})^2}{2}}\mathrm{d}x\\
&\overset{t=\frac{x-4}{2}}{=\!=\!=\!=}\frac{1}{4\sqrt{2\pi}}\int_{-\infty}^{+\infty}(2t+4)e^{-\frac{1}{2}t^2}\mathrm{d}(2t+4)\\
&=2
\end{aligned}
$$
令 $Y=Xe^{2X}$,则
$$
\begin{aligned}
E(Y)=E(g(X))&=\int_{-\infty}^{+\infty}xe^{2x}\cdot \varphi(x)\mathrm{d}x\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}xe^{2x-\frac{1}{2}x^2}\mathrm{d}x\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}xe^{-\frac{1}{2}(x-2)^2+2}\mathrm{d}x\\
&=2e^2
\end{aligned}
$$
设 $Z$ 表示每周利润,那么 $Z$ 是一个 $(X,Y)$ 的二元函数:
$$
Z=g(X,Y)=\begin{cases}
1000Y & X\ge Y\\
1000X+500(Y-X) & X\lt Y
\end{cases}
$$
然后,由于 $X,Y$ 是相互独立的均匀分布,因此联合概率密度 $f(x,y)$ 就是
$$
f(x,y)=\begin{cases}
\frac{1}{100} & (x,y)\in [10,20]\times[10,20]\\
0 & \text{otherwise}
\end{cases}
$$
因此
$$
\begin{aligned}
E(Z)=E(g(X,Y))&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)\mathrm{d}x\mathrm{d}y\\
&=\int_{10}^{20}\int_{10}^{x}\frac{1}{100}1000y\mathrm{d}y\mathrm{d}x + \int_{10}^{20}\int_{x}^{20}\frac{1}{100}500(x+y)\mathrm{d}y\mathrm{d}x\\
&=\frac{42500}{3}
\end{aligned}
$$
设连续型随机变量 $X_1,X_2$ 相互独立且方差均存在,$X_1$ 与 $X_2$ 的概率密度分别为 $f_1(x),f_2(x)$,随机变量 $Y_1$ 的概率密度为 $f_{Y_1}(y)=\frac{1}{2}[f_1(y)+f_2(y)]$,随机变量 $Y_2=\frac{1}{2}(X_1+X_2)$,则()
- $E(Y_1)\gt E(Y_2),D(Y_1)\gt D(Y_2)$
- $E(Y_1)=E(Y_2),D(Y_1)= D(Y_2)$
- $E(Y_1)=E(Y_2),D(Y_1)\lt D(Y_2)$
- $E(Y_1)=E(Y_2),D(Y_1)\gt D(Y_2)$
$$
\begin{aligned}
E(Y_1)=\int_{-\infty}^{+\infty}yf_{Y_1}(y)\mathrm{d}y&=\int_{-\infty}^{+\infty}\frac{y}{2}[f_1(y)+f_2(y)]\mathrm{d}y\\
&=\frac{1}{2}[E(X_1)+E(X_2)]\\
E(Y_2)=E{\frac{1}{2}(X_1+X_2)}&=\frac{1}{2}[E(X_1)+E(X_2)]
\end{aligned}
$$
因此 $E(Y_1)=E(Y_2)$,然后比较 $D(Y_1)$ 和 $D(Y_2)$,根据方差的性质 $D(X)=E(X^2)-E(X)^2$ 可知我们只需要比较 $E(Y_1^2)$ 和 $E(Y_2^2)$。
$$
\begin{aligned}
E(Y_1^2)=\int_{-\infty}^{+\infty}y^2f_{Y_1}(y)\mathrm{d}y&=\int_{-\infty}^{+\infty}\frac{y^2}{2}[f_1(y)+f_2(y)]\mathrm{d}y\\
&=\frac{1}{2}[E(X_1^2)+E(X_2)^2]\\
E(Y_2^2)=E[\frac{1}{4}(X_1+X_2)^2]&=\frac{1}{4}[E(X_1^2)+E(X_2^2)]+\frac{1}{2}E(X_1)E(X_2)
\end{aligned}
$$
因此
$$
D(Y_2)-D(Y_1)=-\frac{1}{4}E(X_1^2)+\frac{1}{2}E(X_1)E(X_2)-\frac{1}{4}E(X_2)^2=-\frac{1}{4}E(X_1-X_2)^2\lt 0
$$
所以,本题结论是 $E(Y_1)=E(Y_2),D(Y_1)\gt D(Y_2)$。
设随机变量 $(X,Y)$ 相互独立,且 $X,Y\sim E(1)$,记 $U=\max(X,Y),V=\min(X,Y)$。
- 求 $f_V(v)$。
- 求 $E(U+V)$。
子问题1:
$$
\begin{aligned}
F_V(v)=P(\min(X,Y)\le v)&=P(X\le v\cup Y\le v)\\
&=1-P(X\gt v,Y\gt v)\\
&=1-[1-P(X\le v)][1-P(Y\le v)]\\
&=1-[1-F(v)]^2
\end{aligned}
$$
于是 $f_V(v)=F_V(v)^\prime$
$$
f_V(v)=\begin{cases}
2e^{-2v} & v\gt 0\\
0 & v\le 0
\end{cases}
$$
子问题2:
$$
E(U+V)=E(X+Y)=E(X)+E(Y)=\frac{2}{\lambda}=2
$$
$$
D(U)=D(X+Y)=E[(X+Y)^2]-E(X+Y)^2
$$
因此我们分别求解 $E[(X+Y)^2]$ 和 $E(X+Y)$:
$$
\begin{aligned}
E(X+Y)&=\int_{0}^1\int_{1-x}^1 2(x+y)\mathrm{d}x\mathrm{d}{y}\quad 这里因为是均匀分布,所以三角形区域内的概率密度是2\\
&=\frac{4}{3}
\end{aligned}
$$
$$
\begin{aligned}
E[(X+Y)^2]=\int_{0}^1\int_{1-x}^1 2(x+y)^2\mathrm{d}x\mathrm{d}{y}=\frac{11}{6}
\end{aligned}
$$
因此 $D(U)=\frac{1}{18}$。
博主居然比我小一届哇,两年前经常在博客园看你的博客,加油呀∠( ᐛ 」∠)_