平面图形面积
直角坐标系
直角坐标系下计算平面图形面积是最基础的定积分应用(因为这就是定积分的几何意义)。
计算由两条抛物线:$y^2=x,y=x^2$ 所围成的图形的面积。
先确定两抛物线的角点,联立方程组:
$$
\begin{cases}
y^2=x\\
y=x^2
\end{cases}
\Rightarrow (0,0);(1,1)
$$
于是围成的面积即定积分 $\int_0^1 (\sqrt{x} – x^2)\mathrm{d}x = \frac{1}{3}$ 。
求椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2}=1$ 所围成的图形的面积。
由于椭圆关于直角坐标系两个坐标轴都对称,因此我们只需要求第一象限的定积分,然后乘 $4$ 即可。
$$
\begin{aligned}
S &= 4 \int_0^ay \mathrm{d} x
\end{aligned}
$$
这里,利用椭圆的参数方程可以简化运算:
$$
\begin{cases}
x = a\cos t\\
y = b\sin t\\
\end{cases} (0\le t \leq \frac{\pi}{2})
$$
代入 $S = 4 \int_0^ay \mathrm{d} x$ :
$$
\begin{aligned}
S &= 4 \int_0^ay \mathrm{d} x\\
&= 4\int_\frac{\pi}{2}^0 b\sin t \mathrm{d} a\cos t\\
&= 4ab\int_0^{\frac{\pi}{2}}\sin^2 t\mathrm{d} t\\
&= \pi ab \quad (\text{Wallis Formula})
\end{aligned}
$$
极坐标系
极坐标和直角坐标的不同点在于:一个微元现在不是一个曲边梯形,而是随角度转过的一段曲边扇形,如下图。
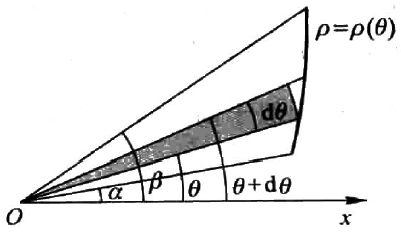
因此一个微元的微分就可以表示为扇形的面积:$\mathrm{d}A = \frac{1}{2}R^2\mathrm{d}\theta$ 。于是,极坐标系下的平面图像面积就可以表示为:
$$
A=\frac{1}{2}\int_\alpha^\beta \rho^2(\theta) \mathrm{d}\theta\\
$$
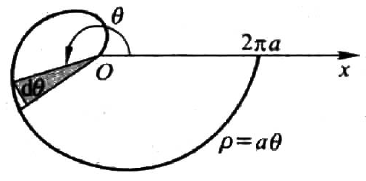
计算阿基米德螺线 $\rho=a\theta(a\gt 0)$ 上相应于 $\theta$ 从 $0$ 变到 $2\pi$ 的一段弧与极轴所围成的图形的面积。
$$
\begin{aligned}
A &= \frac{1}{2}\int_0^{2\pi} a^2\theta^2 \mathrm{d}\theta\\
&= \frac{a^2}{6}\theta^3 \bigg|_0^{2\pi}\\
&= \frac{4}{3}a^2\pi^3
\end{aligned}
$$
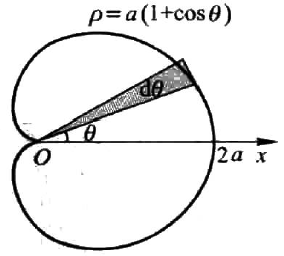
计算心形线 $\rho = a(1 + \cos\theta)\quad (a\gt 0)$ 所围成的图形的面积。
显然,心形线关于 $x$ 轴对称,因此我们只需要计算其一半面积:
$$
\begin{aligned}
A &= 2\times\frac{1}{2}\int_0^\pi a^2(1 + \cos\theta)^2 \mathrm{d}\theta\\
&= a^2\int_0^\pi (1+2\cos \theta + \cos^2\theta)\mathrm{d} \theta\\
&= \frac{3}{2}a^2\pi
\end{aligned}
$$
体积
旋转体的体积
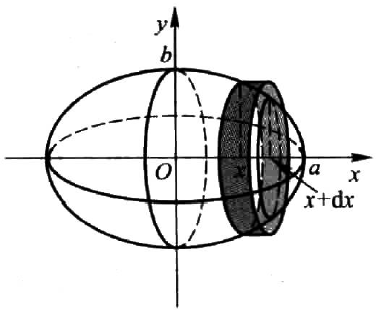
若平面区域 $D$ 由曲线 $y=f(x), (f(x)\ge 0),x=a,x=b(a\lt b)$ 所围成。该平面区域绕 $x$ 轴或 $y$ 轴旋转一周所得到的立体图形就是旋转体,其体积的求法将在下文讨论。
绕x轴的旋转体体积
求体积和面积是类似的,也是找一个微元的意义,如下图:
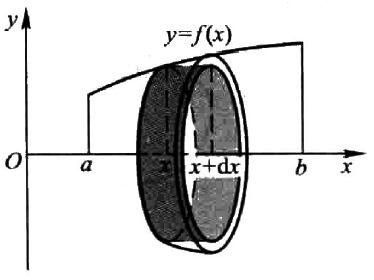
如上图,绕 $x$ 轴旋转体的微元可以近似地看作一个圆柱薄片,因此我们可以据此推出微元的定义:
$$\mathrm{d}V = \pi f^2(x)\mathrm{d}x$$
因此,绕 $x$ 轴的圆柱体体积就是:
$$
V=\pi\int_a^b f^2(x)\mathrm{d}x
$$
计算由椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 所围成的图形绕 $x$ 轴旋转一周而成的旋转体的体积。
由于椭球是对称图形,因此我们只需要计算 $x$ 轴正半轴的体积:
$$
\begin{aligned}
V &= 2\int_0^a f^2(x)\mathrm{d}x\\
&= 2b^2\int_0^a (1-\frac{x^2}{a^2}) \mathrm{d} x\\
&= \frac{4}{3}ab^2\pi
\end{aligned}
$$
绕y轴的旋转体体积
绕 $y$ 轴的旋转体一般有两种观点:方法一就是按照绕 $x$ 轴旋转体那样的方法去做,方法二则是一种更加好的方案,一般称为圆柱壳法,如下图:
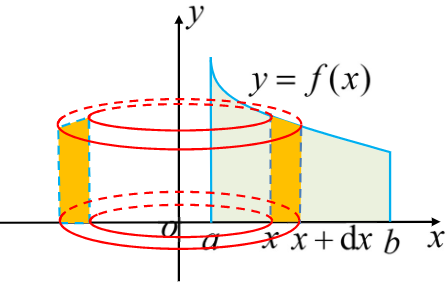
本质上就是:将微元看作一个绕 $y$ 轴旋转一周的细条,那么体积的微分就可以看作是一个圆柱的薄外壳,于是有 $\mathrm{d}V = 2\pi xf(x)\mathrm{d}x$ ,因此绕y轴的旋转体体积也可以写成:
$$V=2\pi\int_a^b xf(x)\mathrm{d}x$$
计算由摆线 $\begin{cases}x=a(t-\sin t)\\ y = a(1-\cos t)\end{cases}$ 相应于 $0\le t\le 2\pi$ 的一拱与直线 $y=0$ 所围成的图形分别绕 $x,y$ 轴旋转而成的旋转体体积。
首先解决绕x轴的旋转体体积问题:
$$
\begin{aligned}
V &= \pi\int_0^{2\pi}a^2(1-\cos t)^2\mathrm{d}a(t-\sin t)\\
&= a^3\pi\int_0^{2\pi}(1-\cos t)^3\mathrm{d}t\\
&= a^3\pi\int_0^{2\pi}(1-(1-2\sin^2\frac{t}{2}))^3\mathrm{d}t\\
&= 32a^3\int_0^{\frac{\pi}{2}}\sin^6t\mathrm{d}t\\
&= 5a^3\pi^2 \quad (\text{Wallis Formula})
\end{aligned}
$$
然后再解决绕 $y$ 轴的旋转体体积问题,如下图所示所求旋转体体积相当于平面区域 $OABC$ 的旋转体体积减去 $OBC$ 的旋转体体积:
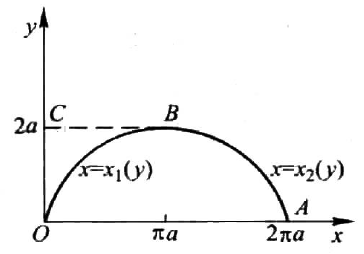
$$
\begin{aligned}
V &= \pi\int_{2\pi}^{\pi}a^2(t-\sin t)^2\mathrm{d}a(1-\cos t) – \pi\int_{0}^{\pi}a^2(t-\sin t)^2\mathrm{d}a(1-\cos t)\\
\end{aligned}
$$
或者用圆柱壳法:
$$
\begin{aligned}
V &= 2\pi\int_0^{2\pi}xf(x)\mathrm{d}x\\
&=2\pi a^3\int_0^{2\pi}(t-\sin t)(1-\cos t)^2\mathrm{d}t\\
&=2\pi a^3\int_{-\pi}^{\pi}(t+\pi-\sin(t+\pi))(\cos(t+\pi)-1)^2\mathrm{d}t\\
&=2\pi a^3\int_{-\pi}^{\pi}(t+\pi+\sin t)(\cos t+1)^2\mathrm{d}t\\
&=2\pi a^3\int_{-\pi}^{\pi}\pi(\cos t+1)^2\mathrm{d}t\\
&=2\pi^2a^3\cdot 4\int_{-\pi}^{\pi}\cos^4 \frac{t}{2} \mathrm{d}t\\
&= 6a^3\pi^3
\end{aligned}
$$
最后的计算结果都是 $6a^3\pi^2$ 。
平行截面面积为已知的立体的体积
这种情况很简单,因为已知截面面积 $A(x)$ ,所以微元就是 $\mathrm{d}V=A(x)\mathrm{d}x$ ,因此:
$$V=\int_a^bA(x)\mathrm{d}x$$
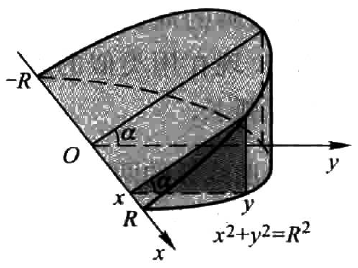
一平面经过半径为 $R$ 的圆柱体的底圆中心,并于地面交成角 $\alpha$ 。计算该平面截圆柱体所得立体的体积。
$$
\begin{aligned}
V &= 2\int_0^R \frac{1}{2}(R^2-x^2)\tan\alpha \mathrm{d}x\\
&=\frac{2}{3}R^3\tan\alpha
\end{aligned}
$$
平面曲线的弧长
直角坐标系
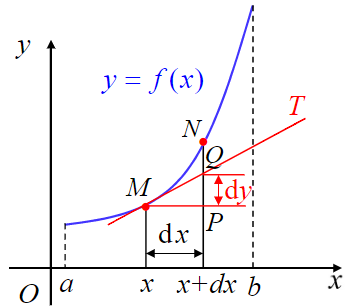
如右图,弧 $MN$ 的微元等价于 $MQ$ ,因此有:
$$
\begin{aligned}
\mathrm{d}L=|MQ|&=\sqrt{(\mathrm{d}x)^2+(\mathrm{d}y)^2}\\
&=\sqrt{1+(\frac{\mathrm{d}y}{\mathrm{d}x})^2}\mathrm{d}x
\end{aligned}
$$
因此,直角坐标系情况下的弧长可以这么计算:
$$L=\int_a^b \sqrt{1+(y^\prime)^2}\mathrm{d}x$$
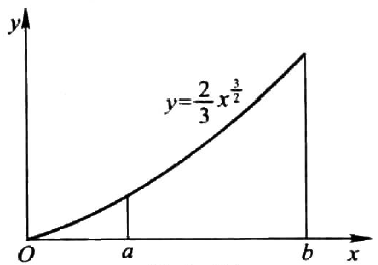
计算曲线 $y=\frac{2}{3}x^{\frac{3}{2}}$ 上相应于 $a\le x\le b$ 的一段弧的长度。
$$
\begin{aligned}
L &= \int_a^b\sqrt{1+(y^\prime)^2}\mathrm{d}x\\
&= \int_a^b\sqrt{1+x}\mathrm{d}x\\
&= \frac{2}{3}(1+x)^{\frac{3}{2}}\bigg|_a^b\\
&= \frac{2}{3}[(1+b)^{\frac{3}{2}}-(1+a)^{\frac{3}{2}}]
\end{aligned}
$$
参数方程
可以从直角坐标系的公式直接类推,假设参数方程为:$\begin{cases}x=\varphi(t)\\ y=\psi(t)\end{cases}$ ,则弧长的微元为:
$$
\begin{aligned}
\mathrm{d}L &= (\mathrm{d}x)^2+(\mathrm{d}y)^2\\
&=\sqrt{(\mathrm{d}t\varphi^\prime(t))^2+(\mathrm{d}t\psi^\prime(t))^2}\\
&=\sqrt{(\varphi^\prime(t))^2+(\psi^\prime(t))^2}\mathrm{d}t
\end{aligned}
$$
因此,参数方程的弧长公式为:
$$L=\int_a^b \sqrt{\varphi^\prime(t)^2+\psi^\prime(t)^2}\mathrm{d}t$$
计算摆线 $\begin{cases}x=a(t-\sin t)\\y=a(1-\cos t)\end{cases}$ 一拱($0\le t\le 2\pi$)的长度。
$$
\begin{aligned}
L &= \int_0^{2\pi}\sqrt{a^2(1-\cos)^2+a^2(-\sin t)^2}\mathrm{d}t\\
&=a\int_0^{2\pi}\sqrt{2-2\cos t}\mathrm{d}t\\
&=2a\int_0^{2\pi}|\sin\frac{t}{2}|\mathrm{d}t\\
&=8a
\end{aligned}
$$
极坐标系
假设曲线弧方程由 $\rho=\rho(\theta)(a\le \theta\le b)$ 确定,根据直角坐标系和极坐标系的关系有:
$$
\begin{cases}
x=\rho(\theta)\cos\theta\\
y=\rho(\theta)\sin\theta\\
\end{cases}
$$
代入弧长的微分,得到:
$$
\begin{aligned}
\mathrm{d}L &= \sqrt{x^\prime(\theta)^2+y^\prime(\theta)^2}\mathrm{d}\theta\\
&= \sqrt{(\rho^\prime(\theta)\cos\theta – \rho(\theta)\sin\theta)^2 + (\rho^\prime(\theta)\sin\theta + \rho(\theta)\cos\theta)^2}\mathrm{d}\theta\\
&= \sqrt{\rho^\prime(\theta)^2+\rho(\theta)^2}\mathrm{d}\theta
\end{aligned}
$$
所以,结论就是:
$$
L=\int_a^b \sqrt{\rho^\prime(\theta)^2+\rho(\theta)^2}\mathrm{d}\theta
$$
求阿基米德螺线 $\rho=a\theta(a\gt 0)$ 相应于 $0\le \theta\le 2\pi$ 一段的弧长。
$$
\begin{aligned}
L&=\int_a^b \sqrt{\rho^\prime(\theta)^2+\rho(\theta)^2}\mathrm{d}\theta\\
&=a\int_a^b \sqrt{1+\theta^2}\mathrm{d}\theta\\
&=a\times (\frac{x}{2}\sqrt{x^2+1}+\frac{1}{2}\ln |x+\sqrt{x^2+1}|)\bigg|_0^{2\pi}\\
&=\frac{a}{2}[2\pi\sqrt{1+4\pi^2}+\ln(2\pi+\sqrt{1+4\pi^2})]
\end{aligned}
$$
旋转体侧面积
直角坐标系
求旋转体侧面积类似于求旋转体体积,需要注意的点是:我们现在是一小段曲线弧绕 $x$ 轴旋转一圈,如下图:
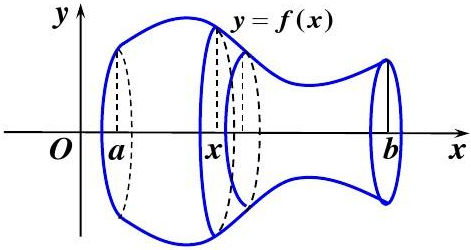
因此,侧面积的微元是:
$$\mathrm{d}A = 2\pi f(x)\mathrm{d}L$$
其中 $\mathrm{d}L$ 就是弧长的微元,因此旋转体的侧面积公式为:
$$
A = \int_a^b 2\pi f(x)\sqrt{1+(y^\prime)^2}\mathrm{d}x
$$
曲线 $y=\sqrt{x-1}$ ,$y=\frac{1}{2}x$ 和 $x$ 轴围成平面区域 $D$ ,求 $D$ 绕 $x$ 轴旋转一周形成的旋转体的表面积。
画一下图,容易发现 $y=\sqrt{x-1}$ 和 $y=\frac{1}{2}x$ 相切于 $(2,1)$ ,并且该旋转体由两部分表面积构成。
$$
\begin{aligned}
A &= 2\pi\int_0^2 \frac{1}{2}\sqrt{1+\frac{1}{2}^2}\mathrm{d}x + 2\pi\int_1^2 \sqrt{1-x}\sqrt{1+(\frac{1}{2\sqrt{x-1}})^2}\mathrm{d}x\\
&= \frac{11\sqrt{5}-1}{6}\pi
\end{aligned}
$$
谢谢大佬
摆线绕y轴旋转体积的最后两步骤有问题答案是6 PI^3 a^3
感谢指出,已修正