注意，本文的主要内容是《算法导论》书中的 KMP 算法，而非原始论文给出的形式。相比较于原始论文，算法导论中给出的 border 形式的 KMP 算法更加实用，原因是 XCPC 竞赛中 border 的作用远超过模式匹配，因此本文中的 next 数组定义为前缀子串最长的 border。

如果你是考研选手，请查阅文末的原始论文定义！！！

Border

先定义两个符号：

1. 字符串 $s$ 长度为 $i+1$ 的前缀子串记为 $pre (s,i)$ 。
2. 字符串 $s$ 长度为 $i+1$ 的后缀子串记为 $suf (s,i)$ 。

例如字符串 $s=ababacab$ 中 $pre (s,3)=aba,suf (s,4)=acab$ 。

Period

Period，即周期。在字符串 $s$ 中，若满足 $s [i]=s [i+p],\forall i\in (0,1,\ldots,|s|-p-1)$ ，则 $p$ 是字符串 $s$ 的一个 period。

Border

Border，可以根据字面意思理解为边界（不知道确切译名）。在字符串 $s$ 中，若满足 $pre (s,p)=suf (s,p)$ ，则 $p$ 是字符串 $s$ 的一个 border，注意 $p<|s|$ ，也就是说某个字符串的 border 不能是它本身。

因此，border 可以理解为：字符串 $s$ 的所有公共前后缀（一个字符串可能有多个 border）。

Period 和 Border 的相互转化

一个推论：如果 $p$ 是字符串 $s$ 的一个 border，那么 $|s|-p$ 是一个 period。这个推论说明 period 和 border 某种意义上是等价的。

前缀函数

给定一个字符串 $s$，其前缀函数被定义为一个长度为 $|s|$ 的数组 $\pi$。
其中 $\pi [i]$ 的定义是：

1. 如果字符串 $s$ 的前缀子串 $pre (s,i)$ 有一对相等的真前缀与真后缀：$pre (pre (s,i),k)$ 和 $suf (pre (s,i),k)$，那么 $\pi [i]$ 就是这个相等的真前缀的长度，也就是 $\pi [i]=k$ 。
2. 如果不止有一对相等的，那么 $\pi [i]$ 就是其中最长的那一对的长度；
3. 如果没有相等的，那么 $\pi [i]=0$。

因此，前缀函数 $\pi [i]$ 实际上就是字符串 $s$ 的前缀 $pre (s,i)$ 中最长的 border。

举例来说，对于字符串 abcabcd：

• $\pi [0]=0$，因为 a 没有真前缀和真后缀，根据规定为 $0$ 。
• $\pi [1]=0$，因为 ab 无相等的真前缀和真后缀。
• $\pi [2]=0$，因为 abc 无相等的真前缀和真后缀。
• $\pi [3]=1$，因为 abca 只有一对相等的真前缀和真后缀：a，长度为 $1$。
• $\pi [4]=2$，因为 abcab 相等的真前缀和真后缀只有 ab，长度为 $2$。
• $\pi [5]=3$，因为 abcabc 相等的真前缀和真后缀只有 abc，长度为 $3$。
• $\pi [6]=0$，因为 abcabcd 无相等的真前缀和真后缀。

因此字符串 abcabcd 的前缀函数为 $[0,0,0,1,2,3,0]$ 。

前缀函数算法实现

在编程实现中，我们一般称前缀函数 $\pi []$ 为 $next []$ 数组，其中 $next [i]$ 表示前缀 $pre (s,i)$ 的最长 border 长度。为了高效求出前缀函数，我们需要一些性质：

• $pre (s,i)$ 是 $pre (s,j)$ 的一个 border $\Leftrightarrow$ $pre (s,i-1)$ 是 $pre (s,j-1)$ 的一个 border 且 $s [i]=s [j]$ 。
• border 具有传递性，假设长度为 $n$ 的字符串 $s$ 的所有 border 长度为 $l_1<l_2<\cdots<l_k$ ，那么可以推出：
  $$\begin{cases} next[n] = l_k\\ next[l_k]=l_{k-1}\\ next[l_{k-1}]=l_{k-2}\\ \cdots\\ \end{cases}$$
• 根据 border 的传递性，可以推出一个迭代关系：$pre (s,i)$ 的所有 border 可以表示为：$next [i],next [next [i]],\ldots$ 。

根据上述性质，如果我们已知 $next [0,1,\ldots,i-1]$ ，想要求出 $next [i]$ ，那就只需要从 $j=next [i-1]$ 开始，每次检查 $s [j]$ 是否等于 $s [i]$ ，如果该条件满足，则说明 $next [i]=j$ ，否则令 $j=next [next [i-1]]$ …… 如此嵌套直到找到前缀函数。

模板

vector<int> getPrefixTable(string& s) {
    int n = s.length();
    vector<int> nxt(n, 0);
    for (int i = 1; i < n; i++) {
        int j = nxt[i - 1];
        while (j > 0 && s[i] != s[j]) {
            j = nxt[j];
        }
        if (s[i] == s[j]) j++;
        nxt[i] = j;
    }
    return nxt;
}

				

					
				
				

					
				
				

					
				
				

					
				
			

时间复杂度分析：注意到 $next [i-1]+1\geq next [i]$ ，因此回跳（$j=next [j]$）的过程最多进行 $O (n)$ 次，所以上述算法是 $O (n)$ 的。

KMP 算法与字符串匹配

对长度为 $n$ 的文本串 $s$ 和长度为 $m (m\leq n)$ 的模式串 $t$ 进行朴素的字符串匹配时，复杂度显然是 $O (nm)$ 的。为了优化这个复杂度，我们可以在失配时利用前缀函数进行跳跃。

在字符串匹配过程中，我们用两个指针 $i,j$ 分别指向文本串和模式串当前匹配到的位置，分两种情况考虑：

1. 当遇到 $s [i+1]= t [j+1]$ 时，说明可以继续匹配，因此两个指针继续往下移动：i++, j++ 。
2. 当遇到 $s [i+1]\neq t [j+1]$ 时，我们已知的信息是 $suf (pre (s,i),j)=pre (t,j)$ ，也就是说他们有一段长度为 $j+1$ 的公共前缀，此时两个指针需要跳转，而非朴素匹配中的归零。 此时，注意到这个公共前缀已经无法匹配，因此我们需要减小 $j$ 指针，此时只需要 check 这个前缀子串的最长 border 能否匹配，如下：
   

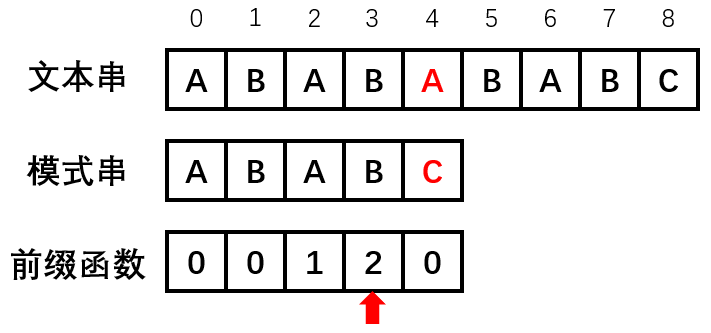
• 上图中演示了 s = ABABABABC, t = ABABC 进行匹配，匹配至 $i=4$ 时失配（$A\neq C$），此时由于已匹配的前缀串 ABAB 的最长 border 是 AB ，因此令 $i=j=4\rightarrow i=4,j=2$ ：

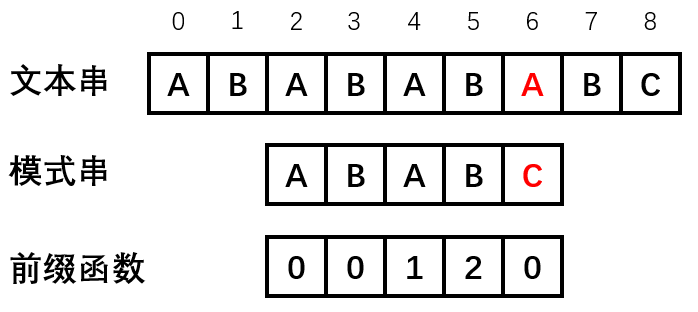
• 如果无法匹配则像求前缀函数时一样嵌套迭代，直到不存在 border 为止。当 $j=m$ 时说明当前位置成功匹配，此时可以逆向算出匹配的位置为 $i+1-m$ ，然后令 $j=next [m-1]$ ，继续下一轮匹配。

最后，当 $j=m$ 时说明当前位置成功匹配，此时可以逆向算出匹配的位置为 $i+1-m$ ，然后令 $j=next [m-1]$ ，继续下一轮匹配。

时间复杂度的分析非常简单，由于每一次匹配操作都会至少使得模式串右移 $1$ 个单位，因此复杂度为 $O (N+M)$ 。

模板

namespace KMP {
    vector<int> getPrefixTable(string& s) { // 求前缀表
        int n = s.length();
        vector<int> nxt(n, 0);
        for (int i = 1; i < n; i++) {
            int j = nxt[i - 1];
            while (j > 0 && s[i] != s[j]) {
                j = nxt[j - 1];
            }
            if (s[i] == s[j]) j++;
            nxt[i] = j;
        }
        return nxt;
    }
 
    vector<int> kmp(string& s, string& t) { // 返回所有匹配位置的集合
        int n = s.length(), m = t.length();
        vector<int> res;
        vector<int> nxt = getPrefixTable(t);
        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && j < m && s[i] != t[j]) {
                j = nxt[j - 1];
            }
            if (s[i] == t[j]) j++;
            if (j == m) {
                res.push_back(i + 1 - m);
                j = nxt[m - 1];
            }
        }
        return res;
    }
}

				

					
				
				

					
				
				

					
				
				

					
				
			

应用

字符串匹配

字符串匹配作为最经典的应用，已经在上文中写过了，可以直接去做模板题：P3375 【模板】KMP 字符串匹配。

一些例题：

• CF471D MUH and Cube Walls
• UVA12467 Secret Word
• CF1017E The Supersonic Rocket
• 2021 浙江省赛 L – String Freshman

如果你想要学习字符串匹配问题的进阶，可以参考这篇文章：FFT 解决字符串匹配问题。

Border & Period

在前面已经提到过：字符串中 Border 和 Period 是可以相互转化的，因此我们可以利用 border 解决很多周期相关的问题。

一些例题：

• UVA455 周期串 Periodic Strings
• CF1200E Compress Words
• P3435 [POI2006] OKR-Periods of Words

KMP 算法的两种不同定义

上方给出的 KMP 算法是《算法导论》中的定义，但是需要注意的是：该方法和原始论文的定义是不同的。

原始论文中定义了两种数组 $f [],next []$，其中 $f$ 数组的定义和上文中的前缀函数（$next$ 数组）类似；但是原始论文中的 $next []$ 数组和现在我们常用的前缀函数有明显区别。

f 数组

原始论文中的 $f$ 数组可以近似地看作前缀函数，其定义如下（下标从 $1$ 开始，而不是常见的 $0-index$）：

$$f[j]= \begin{cases} 0 & j=1\\ 前缀子串 s_{1..j-1} 的最长 border+1 & j\neq 1 \end{cases}$$

例如字符串 $abcabcacab$ 的 $f []$ 数组就是：$0,1,1,1,2,3,4,5,1,2$，如下图：

不难发现，$f$ 数组和前缀函数的定义基本上是一致的。

next 数组

注意，$next []$ 数组有时也被国内教材称为 KMP 算法的进一步优化，但是这个说法没什么道理。

原始论文中的 $next []$ 数组才是真正用来在失配时进行跳跃的，其定义就是：模式串在失配后应该跳到哪一位，如下图所示：

其中 $next [j]=0$ 表示：当前位置 $j$ 必然失配，我们应该把模式串的第 $1$ 位滑动到文本串的第 $j+1$ 位再进行匹配。

注意观察 $next []$ 数组和 $f []$ 数组的区别，第一个不同的位置是第 $4$ 位，因此我们举例说明，比如文本串 $s$ 是 $abcbabca$，而模式串 $t$ 是 $abca$，显然当我们匹配到位置 $j=4$ 时 $s_4=b\neq t_4=a$。此时，如果我们按照前文中的前缀函数方法进行匹配（其实和 $f$ 数组一样），我们应该将模式串滑动到他的最长 border 处，这意味着：我们应该用 $t_1$ 对应 $s_4$ ，然后比较 $t_1$ 和 $s_4$。

但是，从上帝视角看，显然有 $t_1=t_4$，因此比较 $t_1$ 和 $s_4$ 这一步是无意义的，实际上我们应该直接用 $t_1$ 去对应 $s_5$。（观察 $next [4]=0$，也就是说明 $j=4$ 这一位必定失配）出现这个无意义比较的原因就是存在 $t_j=t_{f [j]}$，因此原始论文中的 $next []$ 数组的真实定义实际上是：前缀子串的最长 border，并且 $t_j\neq t_{f [j]}$，并且需要循环这一过程（令 $f [j]=f [f [j]]$ ）。

下面举例说明：例如 $abcab$，显然 $f [5]=2$ ，但是 $t [5]=b=t [f [5]]$，因此我们继续检查 $t [f [f [5]]]$ ，此时由于 $t [f [f [5]]]=a\neq b$，因此 $next [5]=1$。