AtCoder Beginner Contest 205

AC Codes

A – kcal

B – Permutation Check

C – POW

大力分类讨论。小心两边取 $\log$ 的操作，因为可能会出现 $\log 0$ 这种情况。

D – Kth Excluded

给定一个大小为 $N$ 的正整数数列 $A$ ，询问不属于数列 $A$ 的第 $K$ 大正整数。多次询问。

对数列 $A$ 排序后，显然可以二分套二分解决。第一层二分查询答案，第二层二分查询比这个答案小的 $A_i$ 数量。

E – White and Black Balls

有 $N$ 个白球，$M$ 个黑球排成一列，设 $w_i$ 表示前 $i$ 个球中白球的数量，$b_i$ 表示前 $i$ 个球中黑球的数量，求满足 $w_i\leq b_i+k$ 的不同排列数量。

$N,M\leq 10^6, 0\leq K\leq N$ 。

把问题转化到二维坐标轴上，从左往右遍历序列，如果遇到白球就向右走一个单位，否则向上走一个单位，从 $(0,0)$ 走到 $(N,M)$ 。那么本题就是求：不穿过直线 $y=x-K$ 的路径数量。

这个问题非常类似于卡特兰数的一个重要应用：路径计数问题。这个问题有一个经典的求法，如下：

考虑容斥，不妨求出由于要穿过 $y=x-K$ 的方案数，因此我们一定会经过点 $C (c, c – K – 1)$ 。然后将点 $(c, c – K – 1)$ 和点 $(N,M)$ 围成的矩形翻转，如下图：

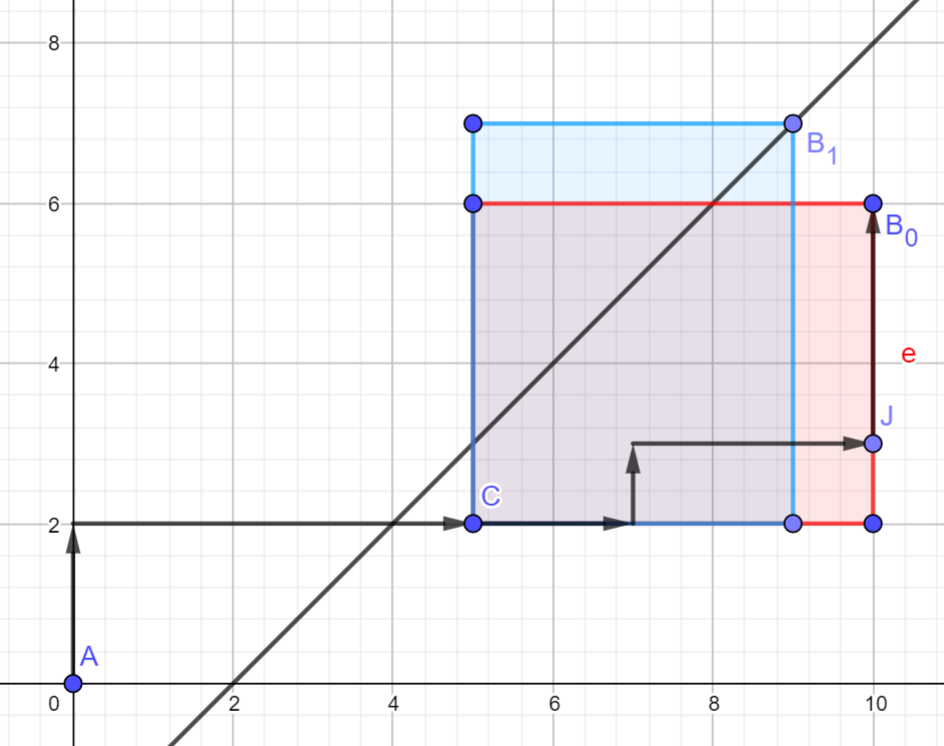
因此我们可以将原本的问题（从 $A$ 走到 $B_0$）转化为从 $A$ 走到 $B_1$ 。由于 $y_{B_0}-y_C=M-(c-K-1),x_{B_0}-x_C=N-c$ ，因此 $B_1$ 的坐标是 $(c+M-(c-K-1),c-K-1+N-c)$ ，化简之后就是 $(M+K+1,N-K-1)$ ，这是一个定点。因此这个问题的方案数就是 $\binom {M+N}{M+K+1}$ 。

再容斥回原本的问题，结论是 $\binom {M+N}{M}-\binom {M+N}{M+K+1}$ ，此外，注意特判一下无解的边界情况。

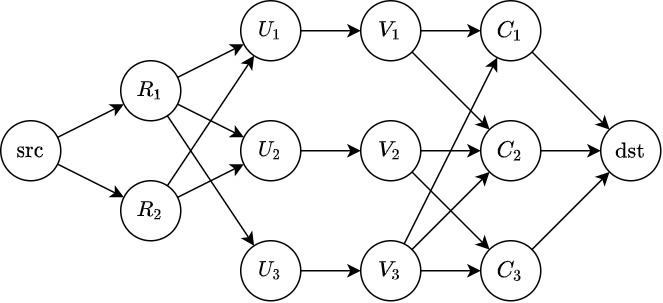
F – Grid and Tokens

给定一个 $H\times W$ 的网格图和 $N$ 枚棋子，第 $i$ 枚棋子可以被放在 $[A_i,C_i]\times [B_i,D_i]$ 这个子矩形中，任意两枚棋子不能位于同一行或列中。询问棋盘上最多可以防止几枚棋子。

$1\leq H,W,N\leq 100$ 。

由于是在网格图上，所以我们可以将一个坐标的横纵两部分拆成二分图，不妨改写一下问题：第 $i$ 枚棋子必须选择第 $a_i,a_{i}+1,\ldots,c_i$ 中的某一行，并且选择 $b_i,b_i+1,\ldots,d_i$ 中 的某一列，每行每列都只能被选中一次，询问最多能放几枚棋子。由于行和列被拆成了两个大小分别为 $H,W$ 的二分图，因此我们可以建图后跑最大流解决本题。

行列只能被选择一次这个限制条件可以通过建图时在二分图的左半部和右半部中间加入一个中间层来解决，具体操作可以参考下图（样例 1 的示意图）：