多项式基本操作
多项式加法、减法
有手就行。
多项式乘法
一句话概括,就是FFT。
这是整个多项式章节中最基础的一部分:如何用FFT将两个 $n$ 度的多项式乘法优化到 $O(n\log n)$ 的时间复杂度。
洛谷模板题:P3803 【模板】多项式乘法(FFT),P4245 【模板】任意模数多项式乘法 。
在多项式乘法中,有两个核心问题,加法卷积和减法卷积:
加法卷积
设 $F(x)=\sum_{i=0}^{n}f_ix^i, G(x)=\sum_{i=0}^{n}g_ix^i$ ,那么就有:
F*G&=\sum_{i=0}^{n}f_ix^i \sum_{i=0}^{n}g_ix^i \\
&=\sum_{k=0}^{2n}\sum_{i+j=k}f_ig_j x^k \\
\end{aligned}
我个人刚学习FFT的时候就没有弄清楚一个很蠢的问题:FFT可以优化多项式乘法,但是这和我卷积有什么关系?实际上卷积和多项式乘法是等价的,并且FFT在大部分的应用场景中都是推出卷积式子后用来优化时间复杂度的。
减法卷积
加法卷积的定义很明确:$\sum_{k=0}^{2n}\sum_{i+j=k}f_ig_j x^k$ ,那么我们怎么求 $\sum_{k=-n}^{n}\sum_{i-j=k}f_ig_j x^k$ 呢?Hugin经常把这个东西叫做减法卷积,虽然网上搜不到这一说法,但是确实很形象,于是我就沿用这一名词。
如下图,给出了加法卷积的图像,不难发现这就是所有满足 $i+j=k$ 的单元格都是一系列反对角线:
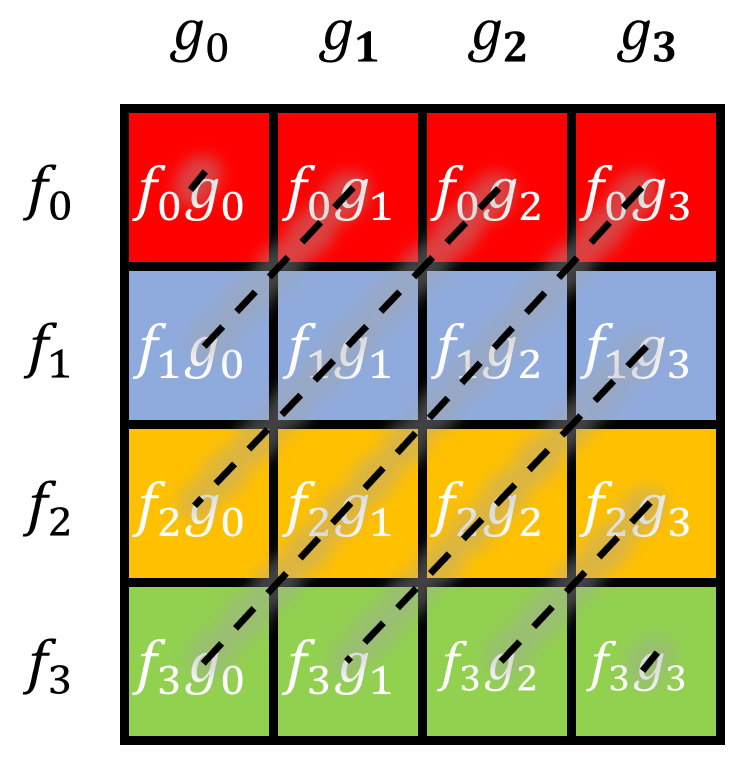
由此,我们也可以画出减法卷积的图像,可以看作加法卷积的水平翻转(也就是一系列对角线):
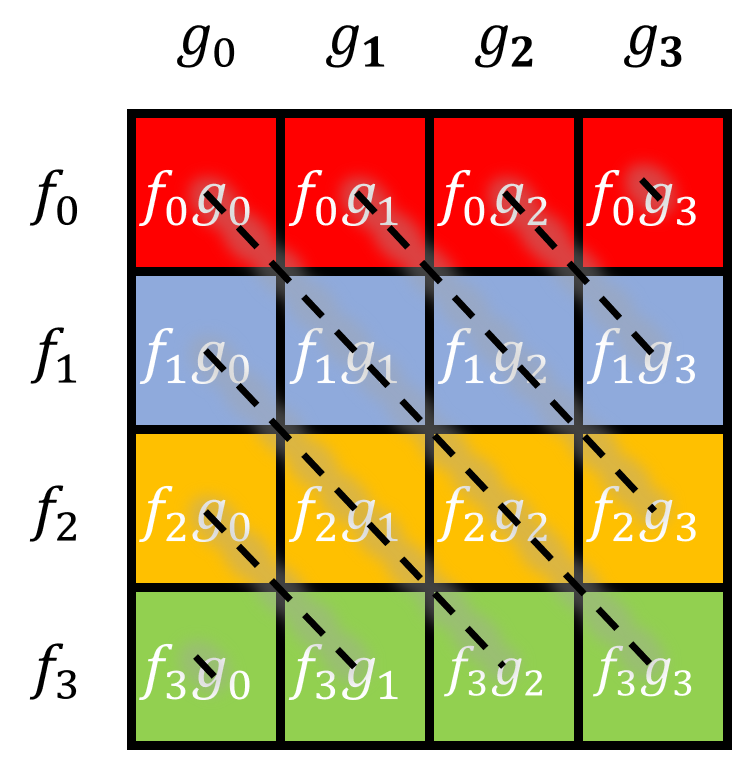
因此,我们可以水平翻转减法卷积,这样减法卷积就完全等价于加法卷积了,如下图(也就是翻转 $G(x)$ 函数):
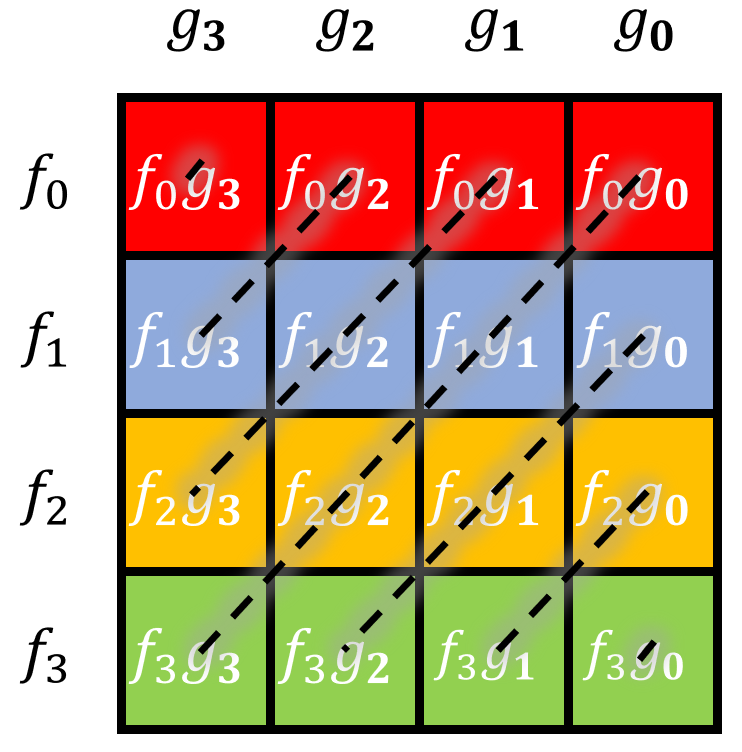
于是,我们记 $G_r(x)=g_n+g_{n-1}x+g_{n-2}x^2+\cdots + g_0x^n$ ,那么减法卷积就是 $F* G_r$ 。
多项式求导
设 $F(x)=\sum_{i=0}^{n}a_ix^i$ ,那么 $F(x)^{\prime}$ 就是:
F(x)^{\prime}=a_1x^0+2a_2x^1+3a_3x^2+\cdots +na_{n}x^{n-1}
\end{aligned}
学过高中数学肯定会。
多项式积分
设 $F(x)=\sum_{i=0}^{N}a_ix^i$ ,那么 $\int F(x)dx$ 就是:
\int F(x)dx=a_0x^1+\frac{a_1}{2}x^2+\frac{a_2}{3}x^3+\cdots + \frac{a_n}{n+1}x^{n+1}+constant
\end{aligned}
其中 $constant$ 是一个常量,我们一般直接忽略,记为 $0$ 。
多项式求逆
已知多项式 $F(x)=\sum_{i=0}^{n-1}a_ix^i$ ,求模 $x^n$ 意义下的多项式逆 $G(x)$ ,即 $F(x)G(x)\equiv 1\pmod{x^n}$ 。
首先,很容易想到由于 $F(x)$ 含有一个常数项 $a_0$ ,因此 $G(x)$ 的常数项一定是 $a_0^{-1}$ 。然后进行数学推导,假设我们已知模 $x^{\lceil\frac{n}{2}\rceil}$ 意义下 $F(x)$ 的逆为 $H(x)$,那就得到了:
F(x)H(x)&\equiv 1\pmod{x^{\lceil\frac{n}{2}\rceil}}\\
F(x)G(x)&\equiv 1\pmod{x^{\lceil\frac{n}{2}\rceil}}
\end{aligned}
两式相减后继续进行推导:
F(x)(G(x)-H(x))&\equiv 0\pmod{x^{\lceil\frac{n}{2}\rceil}}\\
G(x)-H(x)&\equiv 0\pmod{x^{\lceil\frac{n}{2}\rceil}}\\
(G(x)-H(x))^2&\equiv 0\pmod{x^{n}}\\
F(x)(G(x)^2-2G(x)H(x)+H(x)^2)&\equiv F(x)\cdot 0\pmod{x^{n}}\\
G(x)-2H(x)+F(x)H(x)^2&\equiv 0\pmod{x^n}\\
G(x)&\equiv H(x)(2-F(x)H(x))\pmod{x^n}
\end{aligned}
这就得到了一个倍增的做法,时间复杂度 $O(n\log n)$。
洛谷模板题:P4238 【模板】多项式乘法逆 。
多项式开方
这破东西有什么用。
多项式除法
多项式除法一般指长除法,即多项式带余除法。举个例子,假设我们要求 $\frac{F(x)}{G(x)}$ ,不妨转化为:
F(x)=G(x)H(x)+R(x)
\end{aligned}
那么我们要求的就是商 $H(x)$ 和余数 $R(x)$ 。
定义 $F_r(x)$ 为 $F(x)$ 的系数取反后的多项式,即将 $F(x)=\sum_{i=0}^{n}a_ix^i$ 转换为 $F_r(x)=\sum_{i=0}^{n}a_{n-i}x^{i}$ 。假设 $F(x)$ 的最高次数是 $n$ ,$G(x)$ 的最高次数是 $m$ ,因此我们可以有一个推论:$H(x)$ 的最高次数是 $n-m$ ,$R(x)$ 的最高次数不超过 $m-1$ ,于是将 $\frac{1}{x}$ 代入后得到:
F(\frac{1}{x})&=G(\frac{1}{x})H(\frac{1}{x})+R(\frac{1}{x})\\
x^nF(\frac{1}{x})&=x^{m}G(\frac{1}{x})x^{n-m}H(\frac{1}{x})+x^{m-1}R(\frac{1}{x})x^{n-m+1}\\
F_r(x)&=G_r(x)H_r(x)+R_r(x)x^{n-m+1}\\
F_r(x)&\equiv G_r(x)H_r(x)\pmod{x^{n-m+1}}\\
H_r(x)&\equiv \frac{F_r(x)}{G_r(x)}\pmod{x^{n-m+1}}
\end{aligned}
于是,我们就算出了模 $n-m+1$ 意义下的 $H_r(x)$ ,由于 $H(x)$ 的最高次项是 $x^{n-m}$ ,因此我们已经求得了 $H(x)$ ,然后根据 $R(x)=F(x)-G(x)H(x)$ 即可求出余数。
洛谷模板题:P4512 【模板】多项式除法。
多项式对数函数(ln)
已知多项式 $F(x)=\sum_{i=0}^{n-1}a_ix^i$ ,求函数 $G(x)$ 满足 $G(x)\equiv \ln(F(x)) \pmod{x^n}$ 。
首先,若 $ln(F(x))$ 存在,则 $a_0=1$ ,然后直接两边求导再积分:
G(x)^{\prime}&\equiv \ln(F(x))^{\prime} \pmod{x^n}\\
\int G(x)^{\prime}dx&\equiv \int \frac{F(x)^{\prime}}{F(x)}dx \pmod{x^n}\\
G(x)&\equiv \int \frac{F(x)^{\prime}}{F(x)}dx \pmod{x^n}
\end{aligned}
因此,我们只需要对 $F(x)$ 求一次导,然后求 $F(x)$ 的逆,再做一个多项式乘法 $F(x)^{\prime}F(x)^{-1}$ ,最后求一次积分即可,时间复杂度 $O(n\log n)$ 。
洛谷模板题:P4725 【模板】多项式对数函数(多项式 ln) 。
多项式指数函数(exp)
已知多项式 $F(x)=\sum_{i=0}^{n-1}a_ix^i$ ,求函数 $G(x)$ 满足 $G(x)\equiv e^{F(x)} \pmod{x^n}$ 。
多项式快速幂
已知多项式 $F(x)=\sum_{i=0}^{n-1}a_ix^i$ ,求函数 $G(x)$ 满足 $G(x)\equiv F(x)^{k} \pmod{x^n}$ 。
当 $a_0=1$ 时,显然有:
F(x)^k &\equiv \exp(k\ln(F(x)) \pmod{x^n}
\end{aligned}
当 $a_0\neq 1$ 时,我们需要找到系数不为 $0$ 的最低项 $a_{m}x^{m}$ ,然后有:
F(x)^k &\equiv (a_{m}x^{m})^k \exp(k \ln(\frac{F(x)}{a_mx^m})) \pmod{x^n}
\end{aligned}