2021“MINIEYE杯”中国大学生算法设计超级联赛(2)
AC代码
1001 I love cube
给一个三维空间中 $N\times N\times N$ 的点阵,询问一共有几种方法:选出三个点,构成等边三角形,并且每条边平行于坐标平面。
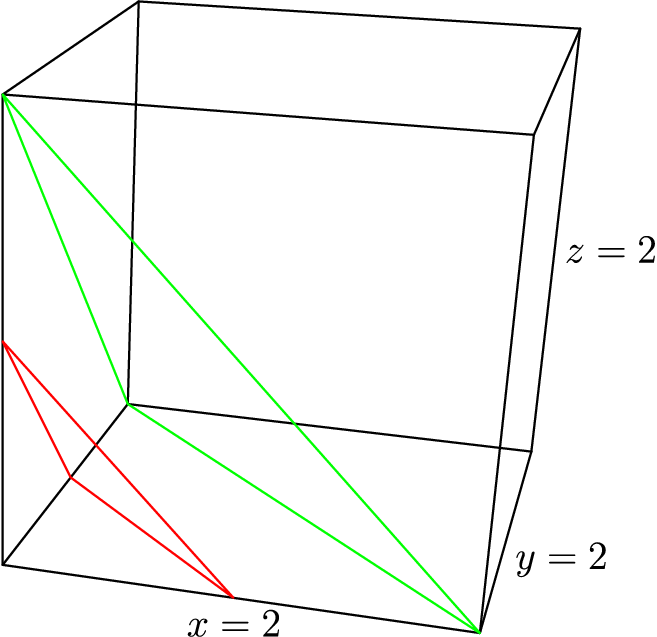
如上图,所以公式是 $(1^3+2^3+\cdots+n^3)\times 8$ 。
1002 I love tree
1004 I love counting
1005 I love string
签到。
1008 I love exam
设 $dp_{i,j,k}$ 表示前 $i$ 门课,挂科 $j$ 门,复习 $k$ 天,最高的得分。
首先预处理出第 $i$门课,复习 $k$ 天的最高得分。
答案为 $dp_{n,p,t}$ 。
1009 I love triples
1010 I love permutation
给定 $a,p$ ,求大小为 $N-1$ 的数列 $A_i\equiv (a\times i)\pmod{p}$ 中的逆序对数的奇偶性。
$p$ 是质数。
最关键的一步转化:
\begin{aligned}
sgn(P) = \frac{\prod_{j>i\geq 0} P_j-P_i}{\prod_{j>i\geq 0}j-i}
\end{aligned}
sgn(P) = \frac{\prod_{j>i\geq 0} P_j-P_i}{\prod_{j>i\geq 0}j-i}
\end{aligned}
其中 $sgn(P)$ 表示逆序对的奇偶性。一个上方式子对于所有排列成立,证明需要考虑两点:
- 这个式子的结果要么是 $-1$ 要么是 $1$ 。这是因为 $\prod_{j>i\geq 0} P_j-P_i$ 和 $\prod_{j>i\geq 0}j-i$ 都是一个 $[1..n]$ 的排列,因此两个式子的绝对值一样,只有正负符号不同。
- 如果该式的结果是 $1$ ,那么该式的逆序对数奇偶性是偶数,否则是奇数。因为 $\prod_{j>i\geq 0}j-i$ 一定是正数(这个式子可以看成在求 $1,2,3,\cdots,n$ 的排列的逆序对数),同时由于交换一对数逆序对数的奇偶性翻转这一性质,因此如果 $\prod_{j>i\geq 0} P_j-P_i$ 是正数则说明 $P$ 的逆序对数奇偶性和 $1,2,3,\cdots,n$ 相同。
有了这步变换就能够推出以下结论了:
\begin{aligned}
sgn(P) &= \frac{\prod_{j>i\geq 0} P_j-P_i}{\prod_{j>i\geq 0}j-i} \\
&\equiv\frac{\prod_{j>i\geq 0}ja-ia}{\prod_{j>i\geq 0}j-i}\pmod{p} \\
&\equiv a^{\frac{P(P-1)}{2}}\pmod{p}
\end{aligned}
sgn(P) &= \frac{\prod_{j>i\geq 0} P_j-P_i}{\prod_{j>i\geq 0}j-i} \\
&\equiv\frac{\prod_{j>i\geq 0}ja-ia}{\prod_{j>i\geq 0}j-i}\pmod{p} \\
&\equiv a^{\frac{P(P-1)}{2}}\pmod{p}
\end{aligned}
所以只需要求出 $a^{\frac{P(P-1)}{2}}\pmod{p}$ 的值即可,更近一步实际上可以求 $a^{\frac{P-1}{2}}\pmod{p}$ 。
1011 I love max and multiply
1012 I love 114514
签到。