2021暑假训练组合数学题解

十二重计数法

• 小球盒子模型大合集

小球盒子模型总结。

「SDOI2016」排列计数

• 错位排列签到题

求有多少种 $1$ 到 $n$ 的排列 $a$，满足序列恰好有 $m$ 个位置 $i$，使得 $a_i = i$ 。

显然就是 $\binom{n}{m}D_{n-m}$ ，$D_i$ 表示 $i$ 的错位排列数量。

CF272D Dima and Two Sequences

• 温暖人心的简单题

给定两个大小为 $N$ 的点对序列 $(a_i,i)$ 和 $(b_i,i)$ ，将两个序列合在一起，重排成一个长度为 $2n$ 的新序列 $c$ ，要求第一维是一个不减序列。询问有几种不同的排列。

$N\leq 10^5$ 。

简单的排列组合，答案显然是 $\frac{\prod cnt_i!}{2^{num}}$ ，其中 $cnt_i$ 表示相同的 $x$ 坐标数量，$num$ 表示完全相同的点对数量。唯一的坑点在于逆元不一定存在。

ABC110D Factorization

• 小球盒子模型+温暖人心的简单题

给定 $N,M$ ，询问有几种长度为 $N$ 且不同的正整数序列 $A$ 满足 $\prod_{i=1}^N A_i=M$ 。

$N\leq 10^5,M\leq 10^9$ 。

将 $M$ 分解质因子为 $p_0^{c_0}p_1^{c_1}\cdots p_k^{c_k}$ ，那么对于每个质因子 $p_i$ 而言都是一个独立的问题：将 $c_i$ 个相同小球放入 $N$ 个不同盒子里，可以空盒有几种方案。乘起来就是答案。

ABC156E Roaming

• 小球盒子模型+温暖人心的简单题

给定 $N,K$ ，一共 $N$ 个房间，每个房间初始有一个人，接下来 $K$ 天中每天恰好移动一个房间中的人，询问最终的不同状态数量。（每个人都看作相同的）。

$N\leq 2\times 10^5,K\leq 10^9$ 。

由于 $N$ 不大，因此可以枚举空房间的数量 $i$ ，剩下的 $N-i$ 个房间可以看作不同的盒子，要放入 $N$ 个小球，不能空盒。因此答案就是 $\sum_{i=0}^{\min(N,K)}\binom{N}{i}\binom{N-1}{N-i-1}$ 。

CF57C Array

• 经典变换

大小为 $n$ 的数列 $a$ 每个元素都满足 $1\leq a_i\leq n$ ，求单调不增或不减的数列数量。

单调不增或不减显然是两种对称的情况，两者当且仅当 $a_1=a_2=a_3=\cdots=a_n$ 的情况下重复计数，因此我们只需要计算其中一种的数量 $S$ ，答案即 $2S-n$ 。

我们考虑计算单调不增的情况，即 $1\leq a_1\leq a_2\leq \cdots\leq a_n\leq n$ 的不同数列数量。我们构造一个辅助数列 $b$ 并且设 $b_i = a_i + i$ ，那么数列 $b$ 就满足 $2\leq b_1<b_2<\cdots<b_n\leq 2n$ ，数列 $b$ 的求解相当容易，显然是 $\binom{2n-1}{n}$ ，因此本题答案为：

ABC205E White and Black Balls

• 卡特兰数

有 $N$ 个白球，$M$ 个黑球排成一列，设 $w_i$ 表示前 $i$ 个球中白球的数量，$b_i$ 表示前 $i$ 个球中黑球的数量，求满足 $w_i\leq b_i+k$ 的不同排列数量。

$N,M\leq 10^6, 0\leq K\leq N$ 。

把问题转化到二维坐标轴上，从左往右遍历序列，如果遇到白球就向右走一个单位，否则向上走一个单位，从 $(0,0)$ 走到 $(N,M)$ 。那么本题就是求：不穿过直线 $y=x-K$ 的路径数量。

这个问题非常类似于卡特兰数的一个重要应用：路径计数问题。这个问题有一个经典的求法，如下：

考虑容斥，不妨求出由于要穿过 $y=x-K$ 的方案数，因此我们一定会经过点 $C(c, c – K – 1)$ 。然后将点 $(c, c – K – 1)$ 和点 $(N,M)$ 围成的矩形翻转，如下图：

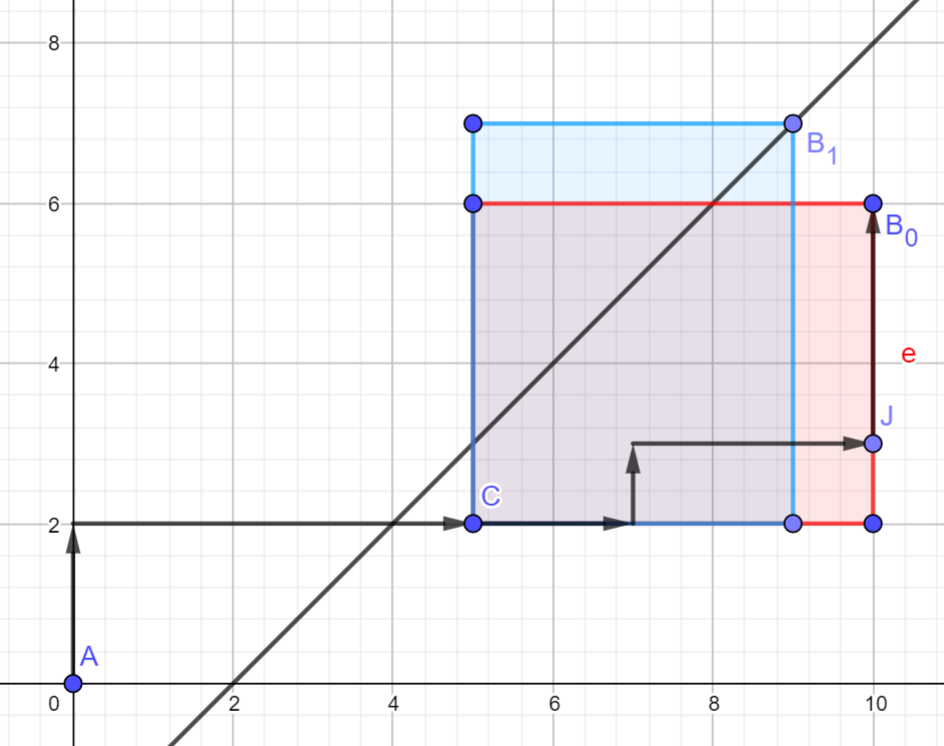
因此我们可以将原本的问题（从 $A$ 走到 $B_0$）转化为从 $A$ 走到 $B_1$ 。由于 $y_{B_0}-y_C=M-(c-K-1),x_{B_0}-x_C=N-c$ ，因此 $B_1$ 的坐标是 $(c+M-(c-K-1),c-K-1+N-c)$ ，化简之后就是 $(M+K+1,N-K-1)$ ，这是一个定点。因此这个问题的方案数就是 $\binom{M+N}{M+K+1}$ 。

再容斥回原本的问题，结论是 $\binom{M+N}{M}-\binom{M+N}{M+K+1}$ ，此外，注意特判一下无解的边界情况。

LeetCode1866 恰有 k 根木棍可以看到的排列数目

• 第一类斯特林数

有 $n$ 根长度互不相同的木棍，长度为从 $1$ 到 $n$ 的整数。请你将这些木棍排成一排，并满足从左侧 可以看到恰好 $k$ 根木棍。从左侧可以看到木棍的前提是这个木棍的左侧不存在比它更长的木棍。

$k\leq n\leq 5000$ 。

将每根能看到的木棍及其后面被挡住的木棍看作一个整体，则这 $n$ 根木棍被划分成了 $k$ 个部分，每个部分的第一根木棍即为可以看到的木棍。

对于每个长为 $m$ 的部分，对于其任意排列，我们总是可以将排列中最大的元素当作可以看到的木棍，移到该部分的开头，则剩余的木棍可以任意排列，因此每个部分的方案数为 $(m-1)!$，即为一个长为 $m$ 的圆排列的方案数。

因此原问题本质上就是在问长为 $n$ 的排列划分成 $k$ 个非空圆排列的方案数，这就是第一类斯特林数。

CF1342E Placing Rooks

• 第二类斯特林数

给定一个 $n\times n$ 的棋盘，要求你在棋盘上放 $n$ 个车（国际象棋），使得所有格子都能被车在一步内攻击到，询问正好存在 $k$ 对车能够相互攻击（不能跨过棋子攻击）的棋子摆法有几种。

$n\leq 200000,k\leq \frac{n(n-1)}{2}$ 。

首先，由于所有格子都需要被车在一步内攻击到，因此该棋盘每一行或者每一列都至少有一个车，由此我们能够立刻推出 $F(n,0)=n!$ 。并且，由于车不能跨过棋子攻击，因此最多存在 $k-1$ 对车能够互相攻击，即 $F(n,k)=0(k\geq n)$ 。

然后，我们考虑存在 $k(n>k>0)$ 对车能够相互攻击的情况，不妨假设该棋盘每一行至少有一个车（和每一列至少有一个车的情况是完全对称的，因此结果乘 $2$ 即可）。我们将这 $n$ 个车看作图上的点，在能够互相攻击的车之间连线，一共需要连 $k$ 条线，因此相当于 $n-k$ 个连通分量，问题转化为将 $n$ 个元素划分为 $n-k$ 个子集有几种方法，实际上就是在求第二类斯特林数 $S^{n-k}_{n}$ 。

由于每一行都至少有一个车，因此只有 $n-k$ 列中有车，相当于在总共 $n$ 列的棋盘中选择 $n-k$ 列，将答案乘上 $C^{n-k}_{n}$ ；并且我们考虑到这 $n-k$ 个子集是无序的，因此再乘上 $(n-k)!$ 。因此本题的答案为 $2S^{n-k}_nC^{n-k}_n(n-k)!$ 。

CF294C Shaass and Lights

• 多重集的排列数

有 $n$ 盏灯，有 $m$ 盏已经点亮，每次只能点亮与已经点亮的灯相邻的灯，求点亮所有灯的总方案数。

$m\leq n\leq 1000$ 。

首先考虑，点亮的灯将整段区间划分为了一堆小区间，每个小区间都可以看作是子问题。除了首尾的两段小区间只有一种点亮方法以外，所有小区间每次点亮的灯既可以是最左侧，又可以是最右侧，因此方案数为 $2^{len-1}$（$len$ 为小区间的长度）。根据乘法原理，这些子问题的乘积 $\prod 2^{len_i-1}$ 就是答案。

但是这样忽略了操作的先后次序，比如有三个区间，操作数分别为 $1,2,3$ ，那我们还需要考虑 $1,2,2,3,3,3$ 这个序列的排列数。设每个子问题都要点亮 $len_i$ 盏灯，这就是一个多重集的排列问题，结论是 $\frac{(\sum len)_i!}{\prod len_i!}$ 。

CF451E Devu and Flowers

• 多重集的组合数+容斥原理

有 $s$ 个球，$n$ 个盒子，第 $i$ 个盒子最多能放 $f_i$ 个球，也可以不放，问放球的方案总数。

$n\leq 20, s\leq 10^{14}, f_i\leq 10^{12}$ 。

多重集的组合数裸题。可以利用容斥原理或dp解决，但是本题的数据范围只能容斥。

改写一下这个问题的表述方式：求方程 $x_1+x_2+x_3+\cdots+x_n=r$ ，且满足 $x_i\leq f_i$ 的约束条件的非负整数解数。

如果我们忽略 $f_i$ 的限制，那么本题就是一个球相同，盒子不同，可以空盒的小球盒子模型，答案是 $\binom{s+n-1}{n-1}$ 。如果我们能求出所有不合题意的方案数，用 $\binom{s+n-1}{n-1}$ 减去就能求出本题答案了。

注意到本题中 $n$ 很小，因此可以直接二进制枚举子集，假设至少某个子集 $S$ 不满足约束条件，也就是说对于任意 $i\in S$ 都满足 $x_i>f_i$ 。对于这个子集 $S$ ，我们可以将 $x_i$ 改写为 $y_i = x_i – (f_i + 1)[i \in S]$ 。这个变换使得问题重新转化为了 $y_1+y_2+\cdots + y_n = S – \sum_{i\in S}(f_i + 1)$ ，于是这又可以套用小球盒子模型解决了。

二进制枚举每个子集，根据子集元素个数的奇偶性进行容斥即可解决本题，复杂度 $O(n\times 2^n)$ 。这题利用二进制枚举进行容斥的思路和这题是一致的。

HHKB2020D Squares

• 容斥原理

多组询问，在 $[0,N]\times [0,N]$ 的平面空间内放入两个边长分别为 $A,B$ 的正方形，顶点均位于整点上且两个正方形不重叠，询问有几种方法？

$A,B\leq N\leq 10^9$ 。

首先，$N<A+B$ 肯定无解，反之有解。

不妨考虑容斥，先不考虑两个正方形重叠的情况，那么答案显然为 $(N-A+1)^2(N-B+1)^2$ ，然后再我们减去这些情况中两个正方形重叠的情况。重叠情况的计数有一个技巧，我们可以将 $x$ 坐标系和 $y$ 坐标系的情况分开来考虑，这样的话就变成了两个相同的一维问题：两条长度分别为 $A,B$ 的线段在 $[0,N]$ 内相交的摆法；二维情况就是一维情况的平方。

这个一维子问题同样可以容斥，我们用不考虑是否重叠情况的总数 $(N-A+1)(N-B+1)$ 减去不重叠的情况数，如果两个线段不重叠，那么整条 $[0,N]$ 的线段一定可以形象地描述为 空格 线段A 空格 线段B 空格 （线段 $A,B$ 位置互换的情况是一致的，结果 $\times 2$ 就行），利用隔板法解决，计算得到结果为：$\binom{N-A-B+2}{2}$。

因此答案为 $(N-A+1)^2(N-B+1)^2-((N-A+1)(N-B+1)-2\binom{N-A-B+2}{2})^2$ 。

CF571A Lengthening Sticks

• 容斥原理

有三根木棍，长度分别为 $a,b,c$ ，你现在可以给这三根木棍加长整数个单位，三根木棍加长的总长不能超过 $l$ ，请问有几种加长方案使得加长后的三根木棍能够围成一个非退化的三角形。

$a,b,c,l\leq 3\times 10^5$ 。

不考虑约束条件的话，总方案数是 $\binom{l+3}{3}$ ，然后我们再减去不合法的情况。分三类讨论： $a$ 为最长边； $b$ 为最长边； $c$ 为最长边。我们先假设 $c$ 是最长边以方便讨论，我们枚举给 $c$ 加上的长度 $i$ ，那么剩下 $\min(l-i,c+i-a-b)$ 的长度分配给 $a,b$ ，显然答案是：

ABC172E NEQ

• 容斥原理

两个大小为 $N$ 的数列 $A,B$ 满足：

1. 对于任意的 $i$ 满足 $A_i\neq B_i$ 。
2. 对于任意的 $i,j(i\neq j)$ 满足 $A_i\neq A_j,B_i\neq B_j$ 。

数列中的每一项都是 $[1,M]$ 的正整数，询问这样的数列数量。

$N\leq M\leq 5\times 10^5$ 。

在满足条件2的情况下，枚举至少有 $i$ 对 $A_j=B_j$ ，那么容易得出这样的数列数量是（设为 $f_i$ ）：

容斥一下就可以得出本题的答案为：$\sum_{i=0}^n (-1)^i f_i$ 。

CF439E Devu and Birthday Celebration

• 容斥原理+小球盒子模型

$q$ 次询问，每次给出 $n,f$ 询问有多少个长度为 $f$ 的不同数列 $a$ 满足：

• 数列 $a$ 元素之和等于 $n$ ，即 $\sum_{i=0}^{n-1}a_i=n$
• 数列 $a$ 各元素的最大公因数为 $1$ ，即 $\gcd(a_0,a_1,\ldots,a_{n-1})=1$ 。

$1\leq f\leq n\leq 10^5, 1\leq q\leq 10^5$ 。

$\gcd=1$ 的数列并不容易直接求，因此我们转化为求 $\gcd\geq i$ 的数列数量，通过容斥原理解决本题。

注意到一个关键点，本题中我们枚举的 $i$ 必定是 $n$ 的因子，而 $10^5$ 以内因子个数最多的数只有 $9592$ 个因子。因此可以枚举每个因子求解。假设当前枚举到的因子是 $i$ ，那么问题就是：求 $\gcd(\frac{a_0}{i}, \frac{a_1}{i},\ldots, \frac{a_{f-1}}{i})\geq \frac{n}{i}$ 的数列数量，这等价于将 $\frac{n}{i}$ 个小球放入 $f$ 个盒子，不能空盒的方案数。

容斥的时候注意，这题的容斥是离散的，不是简单的奇偶翻转。比如 $n=6$ 时，枚举到 $i=1$ ，那么 $1,2,3,6$ 都被计数了，枚举到 $i=2$ ，那么 $2,6$ 都被计数了……

Yukicoder1431 東大文系数学2020第2問改

• 二维容斥原理

二维平面上有 $N$ 条平行于 $x$ 轴的直线和 $N$ 条平行于 $y$ 轴的直线，直线之间互不重合，因此一共有 $N^2$ 个交点。

现在，你可以从这些交点中选择 $M$ 个，并且恰好有 $K$ 条直线不经过任何你选择的点。请问你可以选择的方案数？

$N\leq 3000, M\leq N^2, 0\leq K\leq 2N-2$ 。

枚举有 $i$ 条横线和 $j$ 条竖线上不能选点，那么就只剩下 $(N-i)(N-j)$ 个交点可供选择，因此方案数就是：

但需要注意的是这个方案数实际上对应了 $\binom{i+j}{K}$ 种恰好有 $K$ 条直线不经过任何你选择的点的情况，因此本题的结论是：