编译原理速成

距离期末考试 5 天前的编译原理速成计划。。。

应付简答题的一些概念

编译的逻辑过程

编译的主要逻辑过程有词法分析，语法分析，语义分析，中间代码生成，中间代码优化，目标代码生成，目标代码优化。其间可以有多级中间代码。

编译和解释的区别

编译方式：是将源程序经编译得到可执行文件后，就可脱离源程序和编译程序单独执行，所以编译方式的效率高，执行速度快。
解释方式：在执行时，必须源程序和解释程序同时参与才能运行，其不产生可执行程序文件，效率低，执行速度慢。

文法和语言

文法（grammar）是一个四元组 $G = (V_N, V_T, P, S)$ ，从左到右分别表示非终结符的集合，终结符的集合，产生式的集合和开始符号。

文法 $G [S]$ 的语言 $L (G [S])$ 指的是从该文法的开始符号可以推出的所有只含终结符的字符串集合，用集合的方式可以表示为 $L (G [S]) = \{ x|x\in V_T \cap S \Rightarrow x \}$ 。

四种不同文法的特征：

0 型文法（短语文法，图灵机）
- 产生式形如 $\alpha \rightarrow \beta$
- 其中 $\alpha,\beta \in {(V_T\cup V_N)}^{*}$ 且 $\alpha$ 至少含有一个非终结符
1 型文法（上下文有关文法，线性界限自动机）
- 产生式形如 $\alpha \rightarrow \beta$
- 其中 $|\alpha| \leq |\beta|$ ，仅 $S\rightarrow \varepsilon$ 例外，且 $S$ 不能出现在产生式右部
- 与 0 型文法相比，1 型文法的最大特征就是其产生式左部的长度小于等于右部
2 型文法（上下文无关文法，非确定下推自动机）
- 产生式形如 $A\rightarrow B$
- 其中 $A\in V_N,B\in (V_T\cup V_N)^*$
- 上下文无关文法的最大特征是产生式的左部一定只有非终结符，因此只要找到符合产生式右边的串，就可以把它归约为对应的非终结符
3 型文法（正则文法，有限自动机）
- 产生式形如 $A\rightarrow \alpha$ 或者 $A\rightarrow \alpha B$
- 其中 $\alpha \in V_T^*,A,B\in V_N$

综合属性和继承属性

属性文法中的两类属性，综合属性和继承属性的最大不同之处在于：综合属性是自下而上传递信息的，继承属性是自上而下传递信息的。

S 属性文法和 L 属性文法

S 属性文法只含有综合属性。

L 属性文法既含有综合属性，也含有继承属性，一次自顶向下的遍历就能求出所有值。

平时作业题解

作业 1

T1-1

文法 $G＝(\{A,B,S\},\{a,b,c\},P,S)$ ，其中 $P$ 为
$\begin{cases} S\rightarrow Ac|aB \\ A\rightarrow ab \\ B\rightarrow bc \end{cases}$
写出 $L (G [S])$ 的全部元素。

本题是编译原理中的文法基本概念题，一个文法 $G = (V_N, V_T, P, S)$ 的语言 $L (G [S])$ 指的是从该文法的开始符号可以推出的所有只含终结符的字符串集合。

T1-4

给出生成下述语言的三型文法：
(1) $\{ a^n | n \geq 0 \}$
(2) $\{ a^nb^m|n,m\geq 1 \}$
(3) $\{a^nb^mc^k | n,m,k\geq 0 \}$

就是按照正规文法的定义去构造即可，答案不唯一。

第一问：

\begin{aligned} S\rightarrow aS|\varepsilon \end{aligned}

第二问：

\begin{aligned} S&\rightarrow aA \\ A&\rightarrow aA|B \\ B&\rightarrow bB|b \end{aligned}

第三问：

\begin{aligned} S&\rightarrow aS|A \\ A&\rightarrow bA|B \\ B&\rightarrow cB|\varepsilon \end{aligned}

作业 2

T2-1

构造正规式： $a ((a|b)^* | ab^* a)^* b$ 相应的 DFA.

先画出 NFA：

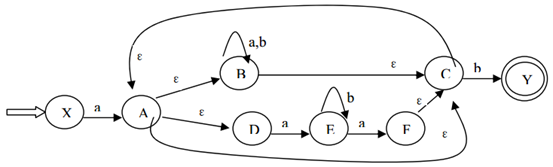
然后利用子集构造法找出 epsilon-closure：

状态名	状态	a	b
0	[X]*	[A,B,C,D]*	/
1	[A,B,C,D]	[A,B,C,D,E]*	[A,B,C,D,Y]*
2	[A,B,C,D,E]	[A,B,C,D,E,F]*	[A,B,C,D,E,Y]*
3	[A,B,C,D,Y]	[A,B,C,D,E]	[A,B,C,D,Y]
4	[A,B,C,D,E,F]	[A,B,C,D,E,F]	[A,B,C,D,E,Y]
5	[A,B,C,D,E,Y]	[A,B,C,D,E,F]	[A,B,C,D,E,Y]

上方表格中带有 * 的表示新状态，需要加入子集表中。

最后根据子集表建立 DFA：

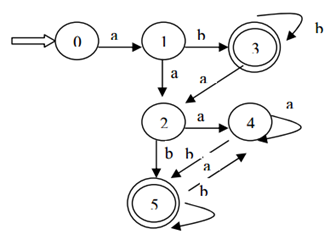
T2-2

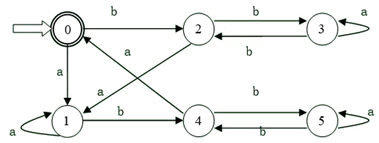
将下图确定化和最小化：

确定化即将非确定性有限自动机（NFA）转化为确定性有限自动机（DFA），而上图已经是一个 DFA，因此不需要执行确定化的步骤，我们直接开始最小化：

根据是否为终态将所有状态分为两个子集： $\{0\}, \{1,2,3,4,5\}$ 。
求出出边 $a$ 的 $\delta$ 函数： $\delta (1,a)=1, \delta (2,a)=1, \delta (3,a)=3, \delta (4,a)=0, \delta (5,a)=5$ 。
求出出边 $b$ 的 $\delta$ 函数： $\delta (1,b)=4, \delta (2,b)=3, \delta (3,b)=2, \delta (4,b)=5, \delta (5,b)=4$ 。
由于 $\delta (4,a)=0$ ，因此 $4$ 不指向集合内部，重新划分为 $\{0\}, \{4\}, \{1,2,3,5\}$ 。
由于 $\delta (1,b)=4,\delta (5,b)=4$ ，因此 $1,5$ 不指向集合内部，重新划分为 $\{0\}, \{1,5\}, \{4\}, \{2,3\}$
由于 $\delta (2,a)=1$ ，因此 $2$ 不指向集合内部，重新划分为 $\{0\}, \{2\}, \{1,5\}, \{3\}, \{4\}$ 。
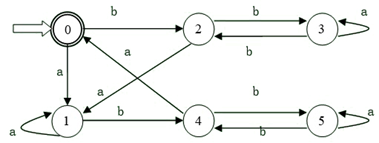
得出一组解： $\{0\}, \{1,5\}, \{2\}, \{3\}, \{4\}$ ，新的状态依次重命名为 $0,1,2,3,4$ ，最后画出最小化 DFA 的图：

$\delta (x,y)$ 函数的意义是状态 $x$ 经过字符 $y$ 到达的新状态。

最小化的本质就是将 DFA 划分为数个所有同类型出边指向相同目标的子集。

作业 3

T3-1

文法为：
$\begin{cases} S\rightarrow a| * |(T) \\ T\rightarrow SN \\ N\rightarrow .SN|\varepsilon \\ \end{cases}$
给出其 LL (1) 分析表，以及输入串 $(a.a)\#$ 的分析过程。

先求出 SELECT 集：

\begin{cases} SELECT(S\rightarrow a)=\{a\} \\ SELECT(S\rightarrow *)=\{*\} \\ SELECT(S\rightarrow (T))=\{(\} \\ SELECT(T\rightarrow SN)=FIRST(S)=\{a,*,(\} \\ SELECT(N\rightarrow .SN)=\{.\} \\ SELECT(N\rightarrow \varepsilon)=FOLLOW(N)=FOLLOW(T)=\{)\} \\ \end{cases}

根据 SELECT 集求出预测分析表为：

	a	*	(	)	.
S	S→a	S→*	S→(
T	T→SN	T→SN	T→SN
N				N→)	N→.SN

最后按照预测分析表给出分析过程（注意分析栈要给出对应的回文串！）：

分析栈	剩余串	动作 / 产生式
#S	(a.a)#	S→(T)
#)T(	(a.a)#	读入
#)T	a.a)#	T→SN
#)NS	a.a)#	S→a
#)Na	a.a)#	读入
#)N	.a)#	N→.SN
#)NS.	.a)#	读入
#)NS	a)#	S→a
#)Na	a)#	读入
#)N	)#	N→epslion
#)	)#	读入
#	#	ACC

T3-2

消除下面文法的左递归并提取左公共因子，然后判断是否为 LL (1) 文法。
$\begin{aligned} A\rightarrow aABe|a, B\rightarrow Bb|d \end{aligned}$

首先提取左公因子：

\begin{cases} A\rightarrow aC \\ C\rightarrow ABe|\varepsilon \\ B\rightarrow Bb|d \end{cases}

观察后容易发现存在一个直接左递归： $B\rightarrow Bb|d$ ，将其消除即可：

\begin{cases} A\rightarrow aC \\ C\rightarrow ABe|\varepsilon \\ B\rightarrow dD \\ D\rightarrow bD|\varepsilon \end{cases}

判断是否为 LL (1) 文法只需要判断产生式的 SELECT 集是否有交，因此我们求出所有产生式的 SELECT 集：

\begin{cases} SELECT(A)=\{a\} \\ SELECT(C\rightarrow ABe)=FIRST(A)=\{a\} \\ SELECT(C\rightarrow \varepsilon)=FOLLOW(C)=FOLLOW(A)=\{\#,d\} \\ SELECT(B\rightarrow dD)=\{d\} \\ SELECT(D\rightarrow bD)=\{b\} \\ SELECT(D\rightarrow \varepsilon)=FOLLOW(D)=FOLLOW(B)=\{e\} \\ \end{cases}

需要进行判断的分支有两个 $SELECT (C)$ 和 $SELECT (D)$ ，分别有：

\begin{cases} SELECT(C\rightarrow ABe)\cap SELECT(C\rightarrow \varepsilon)=\{a\}\cap \{\#,d\}=\phi \\ SELECT(D\rightarrow bD)\cap SELECT(D\rightarrow \varepsilon)=\{b\}\cap \{e\}=\phi \end{cases}

因此，该文法是 LL (1) 文法。

作业 4

T4-1

已知文法 $A\rightarrow aAd|aAb|\varepsilon$ ，判断该文法是否是 SLR (1) 文法，若是构造相应分析表，并对输入串 $ab\#$ 给出分析过程。

增广文法 $G'[S’]:$

\begin{cases} S’\rightarrow A \\ A\rightarrow aAd \\ A\rightarrow aAb \\ A\rightarrow \varepsilon\\ \end{cases}

由此得到 LR (0) 项目集族及识别活前缀的 DFA，如下图：

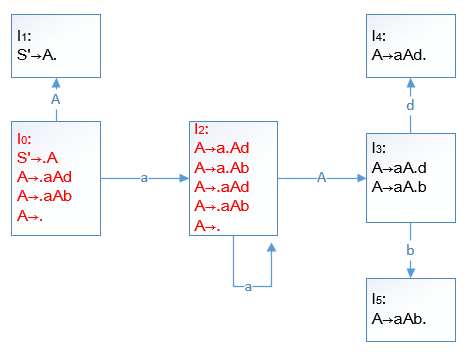
注意上图中标红的 $I_0,I_2$ 中存在移进 - 归约冲突： $A\rightarrow .aAd$ 是移进，而 $A\rightarrow .$ 是归约，因此该文法不是 LR (0) 文法。但是，题目要求的是判断 SLR (1) 文法，因此我们需要判断能否通过 FOLLOW 集解决冲突：

\begin{cases} FOLLOW(A\rightarrow .aAd)=\{d\}\\ FOLLOW(A\rightarrow .aAb)=\{b\}\\ FOLLOW(A\rightarrow .)=\{b,d,\#\}\\ \end{cases}

由于 $\{a\}\cap\{b,d,\#\}=\phi$ ，因此可以用 FOLLOW 集解决移进 - 规约冲突，所以该文法是 SLR (1) 文法，构造分析表如下（其中 a,b,d,# 是 ACTION 表，A 是 GOTO 表）：

状态	a	b	d	#	A
0	S2	r3	r3	r3	1
1				ACC
2	S2	r3	r3	r3	3
3		S5	S4
4		r1	r1	r1
5		r2	r2	r2

根据分析表得到输入串 $ab\#$ 的分析过程：

状态栈	符号栈	剩余输入串	动作
0	#	ab#	S2，移进
02	#a	b#	r3，A→epsilon
023	#aA	b#	S5，移进
0235	#aAb	#	r2
01	#A	#	ACC

作业 5

T5-1

设文法如下 $S\rightarrow L.L | L, L\rightarrow LB | B, B→0 | 1$ ， $S.val$ 为由 $S$ 生成的二进制数的值 (如，对于输入 $101.101$ ， $S.val=5.625$ )；按照语法制导翻译的方法，对每个产生式给出相应的语义规则。

这种题的关键是记住推理的顺序是自底向上的，也就是在回溯时向上合并叶子节点信息！！！可以类比为线段树的 push_up 操作！！！

\begin{cases} S\rightarrow L_1.L_2 & \{S.val:=L_1.val+\frac{L_2.val}{2^{L_2.length}}; print(S.val) \}\\ S\rightarrow L & \{S.val := L.val; print(S.val)\}\\ L_1\rightarrow L_2B & \{L_1.val:=2\times L_2.val+B.val; L_1.length:=L_2.length+1\}\\ L\rightarrow B & \{L.val := B.val;L.length=1\}\\ B\rightarrow 1 & \{B.val:=1\}\\ B\rightarrow 0 & \{B.val:=0\} \end{cases}

上述分析过程中几个需要注意的地方：
1. 开始符需要加一句 $print (S)$ 。
2. 存在多个相同符号时（例如 $S\rightarrow L.L$ ），每个符号要加上下标加以区别。
3. 上方的例子中由于无法在 $S\rightarrow L.L$ 归约前判断到底是整数部分还是小数部分，因此我们需要记录当前二进制数的位数（即 $length$ 属性）
4. 赋值符号是 := 。

T5-2

假设变量的说明是由下列文法生成的： $D\rightarrow i L, L\rightarrow ,i L | :T, T\rightarrow integer | real$ ，建立一个语法制导定义，把每一个标志符的类型加在符号表中。

这题如果代入的是 C 系列语言视角还是挺迷惑的，因为我们定义变量是这么做的：int a，而不是 a:int，但是这个定义方式也是广泛存在的，比如 kotlin 中定义变量就是这样：var a: int 。想通这一点后，这个变量说明文法就迎刃而解了。

此外这一题需要一些前置的定义，我们定义： $type$ 表示变量的类型属性，这显然是一个综合属性； $i.entry$ 代表变量 $i$ 在符号表中的表项； $addtype (x, y)$ 表示将属性 $y$ 添加到变量 $x$ 的表项（符号表）。

\begin{cases} D\rightarrow iL & \{D.type:=L.type;addtype(i.entry, D.type)\}\\ L_1\rightarrow ,iL_2 & \{L_1.type:=L_2.type;addtype(i.entry,L_1.type\}\\ L\rightarrow :T & \{L.type:=T.type\}\\ T\rightarrow integer & \{T.type:=integer\}\\ T\rightarrow real & \{T.type:=real\}\\ \end{cases}

一些重点

最左推导及其语法树

例题：对于上下文无关文法 $G=(\{E,O\}, \{ (, ),＋, *, v, d \}, P, E)$ , $P$ 为
$\begin{cases} E\rightarrow EOE \\ E\rightarrow (E) \\ E\rightarrow v \\ E\rightarrow d \\ O \rightarrow ＋ \\ O \rightarrow * \\ \end{cases}$
给出符号串 $v*(v＋d)$ 的最左推导.

\begin{aligned} E&\Rightarrow EOE \\ &\Rightarrow vOE\\ &\Rightarrow v*E\\ &\Rightarrow v*(E)\\ &\Rightarrow v*(EOE)\\ &\Rightarrow v*(vOE)\\ &\Rightarrow v*(v+E)\\ &\Rightarrow v*(v+d) \end{aligned}

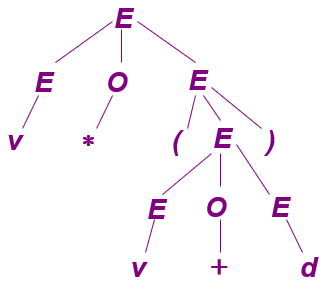
正则表达式和正则文法

由于正则表达式和正则文法是等价的，因此一定可以将两者相互转化。

正则表达式转正则文法的方法如下：
1. 对形如 $A→xy$ 的正规产生式，改写为： $A\rightarrow xB, B\rightarrow y$ ， $B$ 为新的非终结符；
2. 对形如 $A\rightarrow x^*y$ 的正规产生式，改写为： $A\rightarrow y, A\rightarrow xB, B\rightarrow xB, B\rightarrow y$ ， $B$ 为新非终结符；
3. 对形如 $A\rightarrow x|y$ 的正规产生式，改写为： $A\rightarrow x, A\rightarrow y$ ；

例题：将 $r=a (a|d)^*$ 转换为正规文法。

\begin{aligned} S&\rightarrow aA, A\rightarrow (a|d)^* \\ S&\rightarrow aA, A\rightarrow \varepsilon, A\rightarrow (a|d)A \\ S&\rightarrow aA, A\rightarrow \varepsilon, A\rightarrow aA, A\rightarrow bA \\ \end{aligned}

正则文法转正则表达式方法如下：
1. 文法产生式 $A\rightarrow xB, B\rightarrow y$ ，转换为正规式 $A\rightarrow xy$ 。
2. 文法产生式 $A\rightarrow, xA|y$ ，转换为正规式 $A\rightarrow x^*y$ 。
3. 文法产生式 $A\rightarrow x, A\rightarrow y$ ，转换为正规式 $A\rightarrow x|y$ 。

例题：文法 $G [S]: S\rightarrow aA,S\rightarrow a, A\rightarrow aA, A\rightarrow dA, A\rightarrow a, A\rightarrow d$ 转换为正规式。

将 $S,A$ 为左部的产生式分别列出： $S\rightarrow aA|a, A\rightarrow (a|d) A|(a|d)$
推出 $A\rightarrow (a|d)^*$
推出 $S\rightarrow a (a|d)^*$

左递归

最简单的左递归就是形如 $S\rightarrow Sa|b$ 的文法，这时会导致不断调用 $S\rightarrow Sa$ 这一产生式，使得无法进行文法识别。

消除直接左递归的方法：

对形如 $P\rightarrow P\alpha | \beta$ 的产生式，可以修改为 $P\rightarrow \beta Q, Q\rightarrow \alpha Q | \varepsilon$ 。其中 $Q$ 为新增加的非终结符。

例题：消除文法 $G [E]: E\rightarrow E+T|T, T\rightarrow T*F|F, F\rightarrow (E)|a$ 的左递归。

本题中很显然有两个左递归（前两个式子），因此只需要修改这两个产生式：

\begin{cases} E\rightarrow TA \\ A\rightarrow +TA|\varepsilon \\ T\rightarrow FB \\ B\rightarrow *FB|\varepsilon \\ F\rightarrow (E)|a \end{cases}

消除间接左递归的方法：

如果有间接左递归，例如 $S\rightarrow Aa|b, A\rightarrow S$ ，我们可以将 $S$ 代入出现了间接左递归的式中将其变为直接左递归。

例题：消除文法 $G [S]: S\rightarrow Aa|b, A\rightarrow Ac|Sd|\varepsilon$ 的左递归。

该文法中存在的间接左递归是 $S\rightarrow Aa, A\rightarrow Sd$ ，因此我们将 $S$ 代入得到： $A\rightarrow Ac|Aad|bd|\varepsilon$ 。

上式中存在两个左递归，分别消除后得到：

\begin{cases} A\rightarrow bdB|B \\ B\rightarrow cB|adB|\varepsilon \end{cases}

FIRST, FOLLOW, SELECT

注意 FIRST 集中可能含有 $\varepsilon$ ，而 FOLLOW 集中一定不含 $\varepsilon$ ，但是可能有 $\#$ ，即终止符号。

LR(0), SLR(1), LR(1)

判断 LR (0) 是最简单的，只需要看是否存在移进 - 归约冲突或者归约 - 归约冲突，若不存在则为 LR (0)。

判断 SLR (1) 的话则需要分类讨论，例如出现了 $A\rightarrow .a | .B$ 的移进 - 归约冲突，则需要判断 $FOLLOW (A)\cap \{a\}$ 是否为空；若出现了 $A\rightarrow .a, B\rightarrow .a$ 的归约 - 归约冲突，则需要判断 $FOLLOW (A)\cap FOLLOW (B)$ 是否为空；两者均为空时则为 SLR (1) 文法。

~~只要不是以上两个，那么一定是 LR (1) 了，因为只剩这个了（LALR 不考）。~~

直接上例题：

已知文法 $G=(\{A,B,D\}，\{a,b\},P,S)$ 其中 $P$ 为： $A\rightarrow BaBb|DbDa,B\rightarrow \varepsilon,D\rightarrow \varepsilon$ 。
(1) 判断 G 是 LR (0)、SLR (1) 还是 LR (1)，请给出原因；
(2) 构造与上述判断文法相应的分析表；
(3) 对输入串 $ab\#$ 给出分析过程.

遇到这种直接问三种文法的题目直接画 LR (1) 自动机是最省事的：

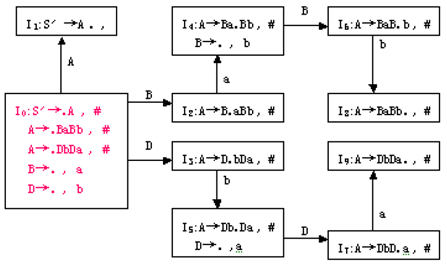
由于 I0 存在移进 - 归约冲突，因此不是 LR (0) 文法。

$I_0$ 存在归约 - 归约冲突，同时 $FOLLOW (B)\cap FOLLOW (D)=\{a,b\}$ ，因此不是 SLR (1) 文法。

注意到 $B\rightarrow .,a$ 和 $D\rightarrow .,b$ 可以通过搜索字符 $a,b$ 区分，因此是 LR (1) 文法。分析表如下：

状态	ACTION			GOTO
	a	b	#	A	B	D
0	R3	R4		1	2	3
1			ACC
2	S4
3		S5
4		R3			6
5	R4					7
6		S8
7	S9
8			R1
9			R2

$ab\#$ 的分析过程如下表：

状态栈	符号栈	剩余输入串	动作	转移
0	#	ab#	R3	2
02	#B	ab#	S4
024	#Ba	b#	R3	6
0246	#BaB	b#	S8
02468	#BaBb	#	R1	1
01	#A	#	acc

静态链和动态链画图

这部分完全没学，面向题目学习一下。。。

例题：由如下类 Pascal 代码，画出 R 第二次激活时的静态链 (存取链) 和动态链 (控制链)。

 program Main( I,O)；
procedure P;
   procedure Q;
      procedure R;
         begin
            … P; …
         end;   /*R*/
      begin
         … R; …
      end;   /*Q*/
   begin
      … Q; …
   end;   /*P*/
procedure S;
   begin
      … P; …
   end;   /*S*/
begin
   … S; …
end.   /*main*/

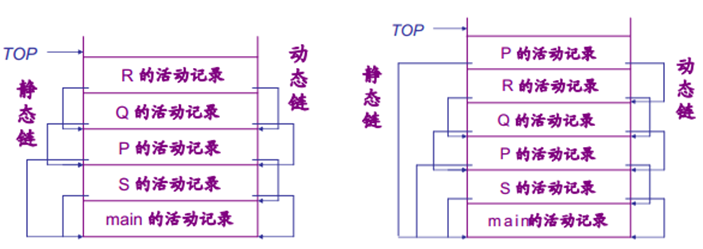
解释一下上图怎么画的：

首先是运行栈的项目由下到上的所有栈中项目都要遵循 pascal 语言自底向上，自外向内的顺序加入。比如 Main 函数是定义在最外层的，因此最先入栈，嵌套的层数为 0；然后入栈的是 P3，嵌套的层数为 1…… 用目录的方法可以这么看：
```
 main
----P
---R
--Q
--P
-S
				
					
				
				
					
				
				
					
				
				
					
				
			
```
因此，总体的顺序就是 `S->P->Q->R->P` 。
静态链的箭头指向指的是定义中的嵌套关系，比如代码中的 P 和 S 都直接定义在 Main 中，因此直接指向 Main；而 Q 定义在 P 中，因此指向 P……
动态链的箭头指向调用自己的函数，比如代码中的 S 直接被 Main 调用，因此指向 Main；P 第一次被 S 调用，因此指向 S；P 第二次被 R 调用，因此指向 R……

流图的一些概念

支配：流图中的节点 $A$ 支配节点 $B$ 表示要到达节点 $B$ 必须先经过节点 $A$ 。记作 A DOM B ，DOM 表示 dominate。
支配节点集：也叫必经节点集，某个节点 $A$ 的支配节点集就是他的所有支配节点的点集。
回边：当点 $A$ 支配点 $B$ 时，如果存在一条 $B$ 到 $A$ 的有向边，这条有向边就被称为回边。
自然循环：当存在一条 $B$ 到 $A$ 的回边时，该回边对应的自然循环就是点 $A$ 和所有从点 $A$ 出发后，不经过点 $A$ 就可以到达点 $B$ 的节点。注意一个特例：如果某个节点存在自环，那么该节点本身构成一个自然循环。

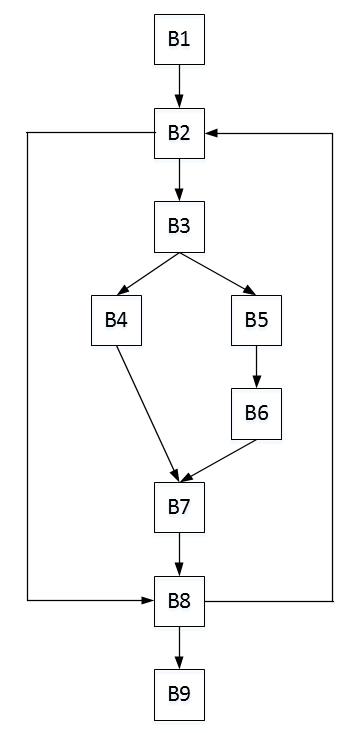
例题：对如下程序流图

(1) 求出流图中各结点 n 的必经结点集 D (n);
(2) 求出流图中的回边；
(3) 求出流图中的循环.