这是Lecture 3 (Part I) – “Manual” Neural Networks和Lecture 3 (Part II) – “Manual” Neural Networks的笔记。
The gradients of a two-layer network
two-layer network
在实际场景下,linear hypothesis class无法分类所有情况,比如
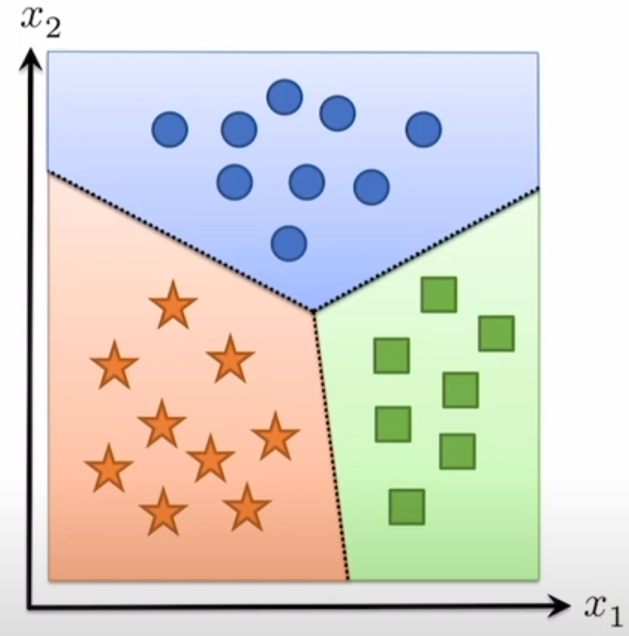
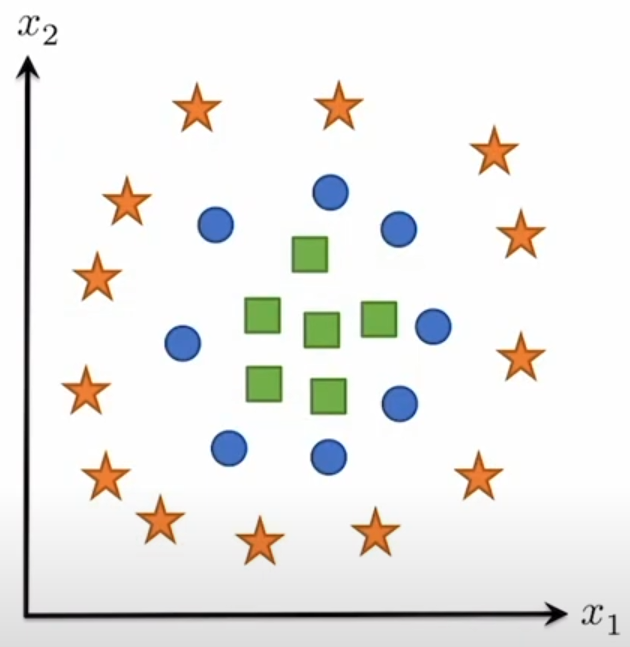
因此往往采用MLP,也就是线性网络+非线性网络嵌套。一个最简单的例子就是two-layer network,
$$
\sigma(XW_1)W_2
$$
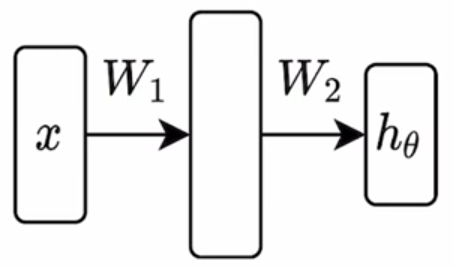
这里 $\sigma$ 表示一个对逐个元素的非线性变换,比如常见的ReLU、tanh等。
$X\in\mathbb R^{m\times n},W_1\in\mathbb R^{n\times d}, W_2\in\mathbb R^{d\times k}$
gradients
令 $X$ 表示输入是batch matrix form。
目标:计算 $\nabla_{{W_1,W_2}}\ell_{ce}(\sigma(XW_1)W_2,y)$。
$W_2$
然后我们还是“将一切视作标量”,直接链式求导,
$$
\begin{aligned}
\frac{\partial \ell_{ce}(\sigma(XW_1)W_2,y)}{\partial W_2} &= \frac{\partial \ell_{ce}(\sigma(XW_1)W_2,y)}{\partial \sigma(XW_1)W_2}\cdot \frac{\partial \sigma(XW_1)W_2}{\partial W_2}\\
&= (S – I_y)\cdot \sigma(XW_1)\quad(S=\text{normalize}(\exp(\sigma(XW_1)W_2)))
\end{aligned}
$$
然后调整维度,$(S-I_y)\in\mathbb R^{m\times k},\sigma(XW_1)\in R^{m\times d}$,而我们是对 $W_2\in\mathbb R^{d\times k}$ 求偏导,因此
$$
\nabla_{W_2}\ell_{ce}(\sigma(XW_1)W_2,y) = (\sigma(XW_1))^T\cdot (S-I_y)
$$
$W_1$
再对 $W_1$ 求偏导,
$$
\begin{aligned}
\frac{\partial \ell_{ce}(\sigma(XW_1)W_2,y)}{\partial W_1} &= \frac{\partial \ell_{ce}(\sigma(XW_1)W_2,y)}{\partial \sigma(XW_1)W_2}\cdot \frac{\partial \sigma(XW_1)W_2}{\partial \sigma(XW_1)}\cdot \frac{\partial \sigma(XW_1)}{\partial XW_1}\cdot \frac{\partial XW_1}{\partial W_1}\\
&= (S-I_y)\cdot W_2\cdot \sigma^\prime(XW_1)\cdot X
\end{aligned}
$$
这里 $\sigma$ 是一个标量函数,所以 $\sigma^\prime$ 就是这个标量函数的导数,比如ReLU的导数就是一个分段函数 $\sigma(x)=0,x\le 0;1,x\gt 0$。
对于上面这一串连乘,我们列出维度:$(S-I_y)\in\mathbb R^{m\times k}, W_2\in\mathbb R^{d\times k}, \sigma^\prime(XW_1)\in\mathbb R^{m\times d}, X\in\mathbb R^{m\times n}$,而 $W_1\in\mathbb R^{n\times d}$,因此
$$
\nabla_{W_1}\ell_{ce}(\sigma(XW_1)W_2,y) = X^T(\sigma^\prime(XW_1) \circ ((S-I_y)W_2^T))
$$
这里 $\circ$ 表示标量积,即逐元素相乘。
这里的启发就是
不要手算了,此外你也很难想到为什么标量积出现在这里,毕竟这不是严谨的数学推导。实际上,我们对于模型求梯度也不会真的手算链式法则,这是最后一次手推特定case的超长链式求导了。
Backpropagation “in general”
假设我们有一个全连接网络 $Z_{i+1} = \sigma_i(Z_iW_i);i=1,\ldots,L$,如果要求最后一层的偏导,那么就有
$$
\frac{\partial \ell(Z_{L+1},y)}{\partial W_i} = \frac{\partial \ell}{\partial Z_{L+1}}\cdot \frac{\partial Z_{L+1}}{\partial Z_L}\cdots \frac{\partial Z_{i+2}}{\partial Z_{i+1}}\cdot \frac{\partial Z_{i+1}}{\partial W_i}
$$
注意到这里的链式求导很多都是重复的操作,设
$$
G_{i+1} = \frac{\partial \ell}{\partial Z_{L+1}}\cdot \frac{\partial Z_{L+1}}{\partial Z_L}\cdots \frac{\partial Z_{i+2}}{\partial Z_{i+1}}
$$
则有一个简单的递推关系
$$
G_i = G_{i+1}\cdot \frac{\partial Z_{i+1}}{\partial Z_i} = G_{i+1}\cdot \frac{\partial \sigma(Z_iW_i)}{\partial Z_iW_i}\cdot\frac{\partial Z_iW_i}{\partial Z_i} = G_{i+1}\cdot \sigma^\prime(Z_iW_i)\cdot W_i
$$
这里 $G_i = \nabla_{Z_i}\ell(Z_{l+1},y)\in\mathbb R^{m\times n_i},Z_i\in\mathbb R^{m\times n_i},W_i\in\mathbb R^{n_i\times n_{i+1}}$。
因此我们调整 $G_{i+1}\cdot \sigma^\prime(Z_iW_i)\cdot W_i$ 的维度为
$$
G_i = \nabla_{Z_i}\ell(Z_{l+1},y) = (G_{i+1}\circ \sigma^\prime(Z_iW_i)) \cdot W_i^T
$$
最后就可以求出我们实际上需要的梯度 $\nabla_{W_i}\ell(Z_{L+1},y)$,
$$
\begin{aligned}
\frac{\partial \ell(Z_{L+1},y)}{\partial W_i} &= \nabla_{W_i}\ell(Z_{L+1},y)\\
&= G_{i+1}\cdot \frac{\partial Z_{i+1}}{\partial W_i}\\
&= G_{i+1}\cdot \frac{\partial \sigma_i(Z_iW_i)}{\partial W_i}\\
&= G_{i+1}\cdot \frac{\partial \sigma_i(Z_iW_i)}{\partial Z_iW_i}\cdot \frac{\partial Z_iW_i}{\partial W_i}\\
&= G_{i+1}\cdot \sigma^\prime(Z_iW_i) \cdot Z_i
\end{aligned}
$$
最后再调整维度为
$$
\frac{\partial \ell(Z_{L+1},y)}{\partial W_i} = \nabla_{W_i}\ell(Z_{L+1},y) = Z_i^T \cdot (G_{i+1}\circ \sigma^\prime(Z_iW_i))
$$
Backpropagation: Forward and backward passes
一次完整的反向传播算法实际上由一次前向传播和一次反向传播共同组成,具体流程如下:
- Forward pass
- Initialize: $Z_1=X$,
- Iterate: $Z_{i+1} = \sigma_i(Z_iW_i); i=1,\ldots,L$。
- Backward pass
- Initialize: $G_{L+1} = \nabla_{Z_{L+1}}\ell(Z_{L+1},y) = S-I_y$,
- Iterate: $G_i = (G_{i+1}\circ \sigma^\prime(Z_iW_i)) \cdot W_i^T; i=L,\ldots,1$,
- Compute gradients: $\nabla_{W_i}\ell(Z_{L+1},y) = Z_i^T \cdot (G_{i+1}\circ \sigma^\prime(Z_iW_i))$。