本文内容主要来源于Transformer原始论文、The Annotated Transformer和CMU Advanced NLP Fall 2024 (4): Attention and Transformers。

Model Architecture

大多数有竞争力的神经序列转换模型（Neural Sequence Transduction Models）都具有编码器-解码器（Encoder-Decoder）结构(cite)。

编码器将输入的符号表示序列 $(x_1,\ldots,x_n)$ 映射到一个连续表示的序列 $\boldsymbol{z}=(z_1,\ldots,z_n)$。

符号表示（Symbol Representations）：

• 在NLP中，符号通常指的是单词、字符或其他离散的语言单位。
• 每个符号 $x_i$ 通常通过嵌入层（Embedding Layer）转换为一个高维向量，这些向量捕捉了符号的语义和语法特征。

输入序列（Input Sequence）：

• 序列中的每个符号 $x_1,\ldots,x_n$ 按照其在句子或文档中的顺序排列。
• 例如，句子 “I love NLP” 的符号序列可以表示为 $(x_1, x_2, x_3) = (\text{I}, \text{love}, \text{NLP})$。

连续表示（Continuous Representations）

• 编码器将每个离散的符号向量 $x_i$ 映射为一个新的连续向量 $z_i$，这些向量位于一个连续的、高维的向量空间中。
• 这些连续向量不仅包含了每个符号的基本特征，还融合了其在序列中的上下文信息。
• 比如原始的文字信息可能采用独热编码（One-Hot Encoding）：

  "cat"   → [1, 0, 0, 0]
  "dog"   → [0, 1, 0, 0]
  "mouse" → [0, 0, 1, 0]

每个向量彼此正交，无法体现“猫”和“狗”在语义上的相似性。

如果采用词嵌入（Word Embedding）则

  "cat"   → [0.2, 0.8, 0.1, ...]
  "dog"   → [0.3, 0.7, 0.2, ...]
  "mouse" → [0.1, 0.9, 0.05, ...]

“cat”和“dog”的向量在空间中距离较近，反映了它们在语义上的相关性。

对于给定的 $\boldsymbol z$，解码器随后逐个元素生成输出符号序列 $(y_1,\ldots,y_m)$。在每一步中，模型都是自动回归（auto-regressive）的(cite)，将前一步中模型生成的符号序列当作一个额外的输入进行处理。

怎么理解自动回归？

这里的自动（auto）其实表现在模型每一层都会将前一层的输出当作输入，也就是在生成 $y_t$ 时，模型会自动利用先前推导的信息 $y_1,\ldots,y_{t-1}$，而无需人为设置参数进行干预。

下方代码给出了一个编码器-解码器架构模型的基本实现：

class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many
    other models.
    """

    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator

    def forward(self, src, tgt, src_mask, tgt_mask):
        """Take in and process masked src and target sequences."""
        return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)

    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)

    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

class Generator(nn.Module):
    """Define standard linear + softmax generation step."""

    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        return log_softmax(self.proj(x), dim=-1)

Transformer 遵循这一整体架构，对编码器和解码器使用堆叠的self-attention和FFN层，分别如图 1 的左半部分和右半部分所示。

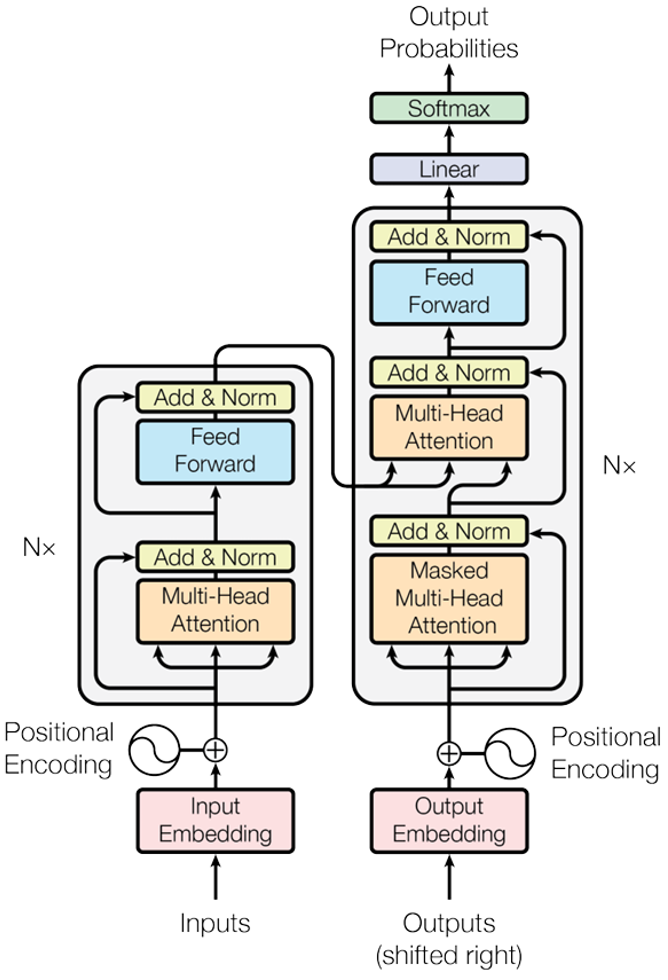
Multi-Head Attention

Attention

先看原文中的定义：

一个注意力函数可以被描述为将一个查询（query）和一组键值对（key-value pairs）映射到一个输出，其中查询、键、值和输出都是向量。输出是通过对值的加权求和计算得到的，其中每个值的权重是通过查询与对应的键的兼容性函数来计算的。

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

啥玩意？先往下看……

Cross-Attention和Self-Attention

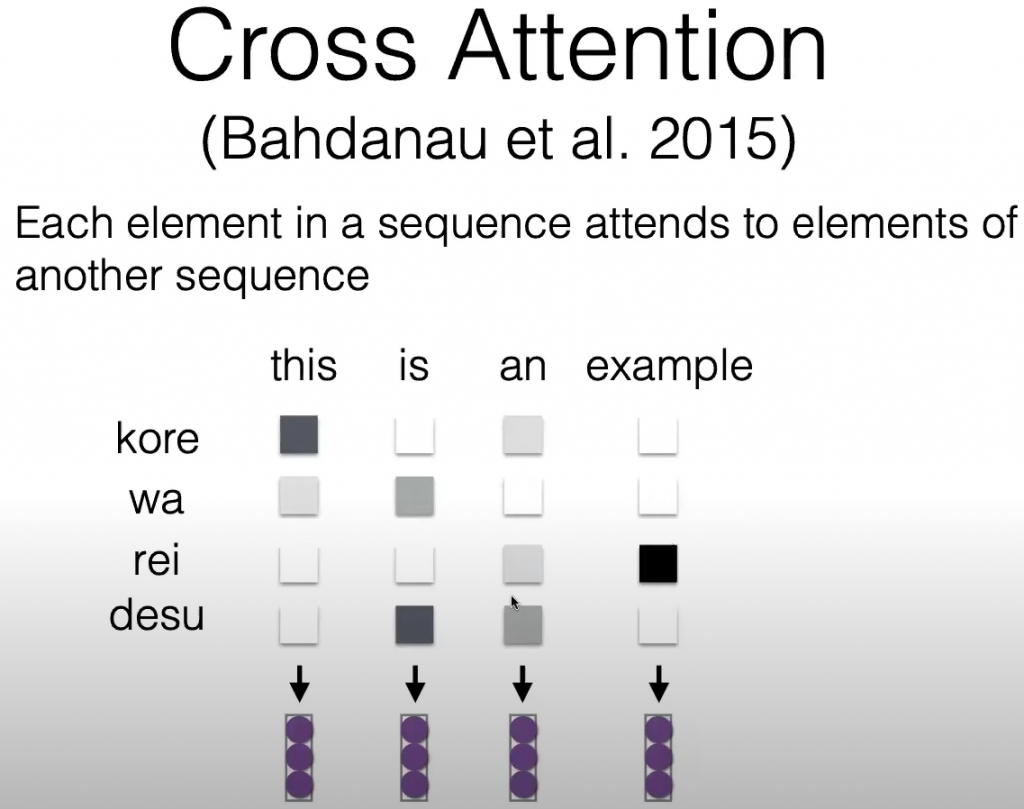
简单地，cross-attention用于衡量两个不同序列之间的对应关系（或者说我们应该“注意”的对象），比如上图实际上给出了一个日语-英语翻译的例子，颜色越深表示这两个对象之间的关系越紧密。而self-attention则用于衡量相同序列之间的对应关系。

Calculating Attention

我们通过一个日语-英语翻译的例子来解释注意力（attention）的概念，由于是两个不同序列，因此这个例子是cross-attention：将日语“kono eiga ga kirai”翻译到英语“I hate this movie”。

“kono eiga ga kirai” 是日语中的一个常用短语，意思是“我讨厌这部电影”或“我不喜欢这部电影”。

この (kono)：

• 意思：这个、这。

映画 (eiga)：

• 意思：电影、影片。

が (ga)：

• 意思：是（日语中的主格助词）。

嫌い (kirai)：

• 意思：讨厌、不喜欢。

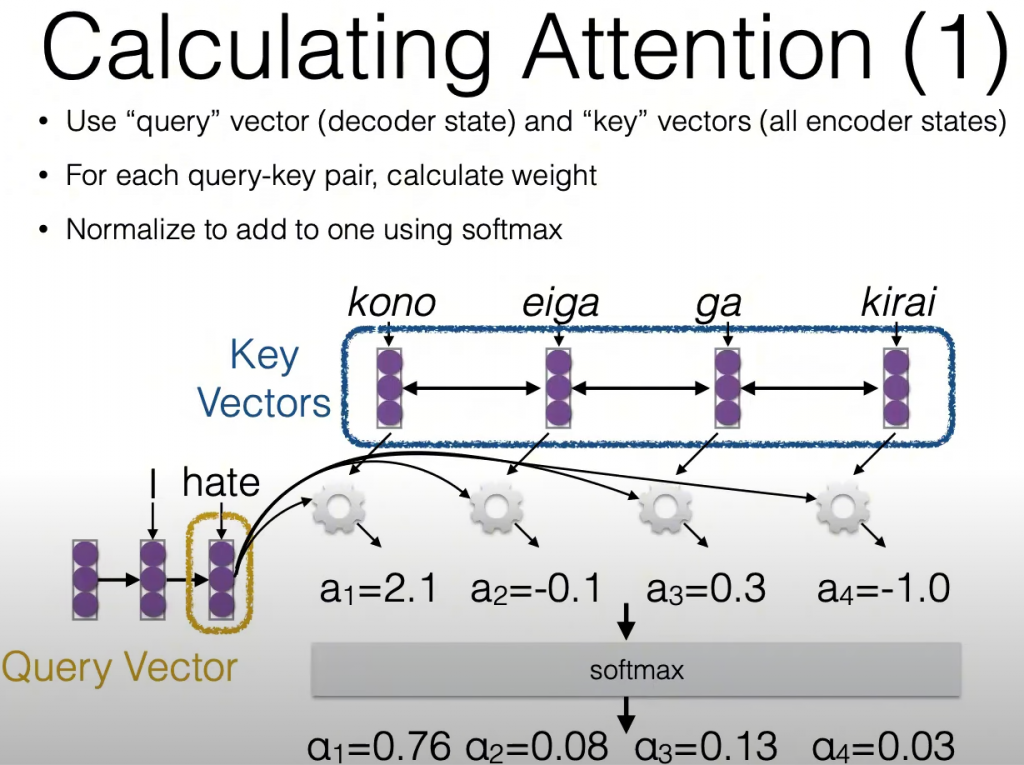
图中的示例是当前查询到 hate 这个单词的状态下（query vector，注意这个vector实际上也包含之前状态I的信息，并不仅仅是hate这个token），或者说我们的模型已经翻译出了 I hate；在kono eiga ga kirai（key vectors）中，接下来应该“注意”哪些vector。

因为当前状态（query vector）已经包含了I hate的信息，所以我们下一步自然应该更加关注this在日语中的对应关系，即kono（图中的数值也表明了我们的推理是合理的）。

最后再通过一个softmax以归一化数值范围，就可得到对于query vector我们更应该“注意”哪些key vectors了，如上图sample为 0.76, 0.08, 0.13, 0.03。

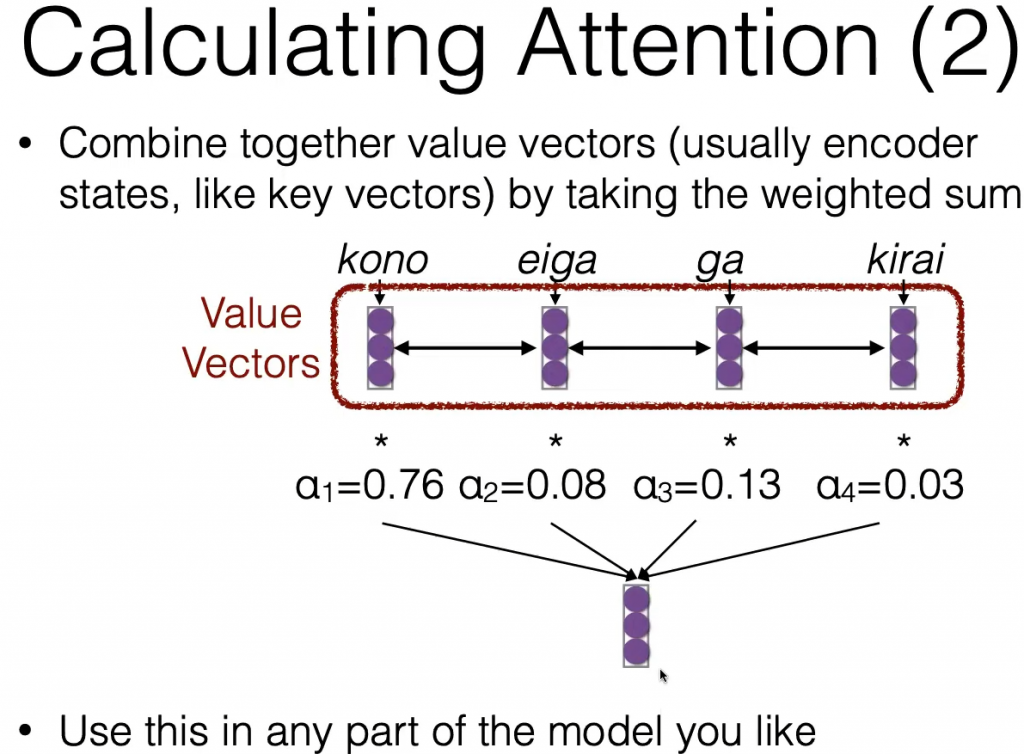
在求出了当前的query vector对于每一个key vector的“注意”程度（也就是 0.76, 0.08, 0.13, 0.03 这个概率）之后，再对value vectors加权求和就能得到最终所求结果了。注意在大部分情况下，value vectors一般等于key vectors。

也就是说，不论在cross-attention中还是self-attention中都有 $k=v$，它们的区别就在于：

• self-attention: $q=k$
• cross-attention: $q\neq k$

因此，我们可以得到attention的一个直观理解：求出在当前状态下（query vector）我们应该“关注”的内容（对key vectors中的每个vector加权求和）。

Attention Score Functions

我们已经通过一个例子了解了attention的概念，包括Cross-Attention和Self-Attention的区别，但是我们还没有解决一个问题：怎么计算attention（比如上图中的 0.76, 0.08, 0.13, 0.03），这就引出了这一节的内容：Attention Score Functions。

一个简单好用的方法就是采用MLP去计算 $Q$ 和 $K$ 之间的attention，MLP的简单结构可以表示出各种复杂的函数关系，这是一个非常灵活的方法。

但是，MLP存在一个严重问题：难以表达两个vector之间的点积（并不是不行），这是因为MLP引入了非线性变换。但是在NLP中我们很直观地希望看到：两个相似单词的vector也应该相近，因此它们之间的点积也应该更大；而词义相差较大的单词之间的点积则应该尽量小。

一个简单的解决方案就是上图中的bilinear score function，这个方法去掉了非线性变换，且仅仅只引入了一个矩阵作为参数。

那么为什么不直接用点积呢？

假设 $Q,K$ 是两个不等长但相似的序列，直接用点乘就无法准确表示他们之间的关系了！并且点乘没有参数，不够灵活。

在transformer中实际上用到的是scaled dot product（注意这里只是一个简化，实际上并不仅仅是点积），不难发现它与简单的点积之间的区别就在于：它除以了一个缩放因子 $d_k$，且这个 $d_k = \sqrt{|k|}$。

缩放步骤的引入主要是为了解决以下问题：

1. 梯度消失问题：
   当查询和键向量的维度 $d_k$ 很大时，点积 $q^\text{T}k$ 的值可能会非常大。这会导致 softmax 函数的梯度变得非常小，影响模型的训练效果。
2. 数值稳定性：
   缩放点积有助于保持 softmax 输入的数值范围在一个合理的区间内，避免数值过大或过小导致的计算不稳定。

为什么缩放因子是 $\sqrt{|k|}$？因为这个值的实验结果表现较好。

Scaled Dot-Product Attention

在transformer中，采用了一种特殊的”Scaled Dot-Product Attention”，输入由维度为 $d_k$ 的queies和keys、维度为 $d_v$ 的values构成。这里的Scaled Dot-Product跟上一小节的定义是完全相同的，也就是 $q^\text{T}k / d_k$。

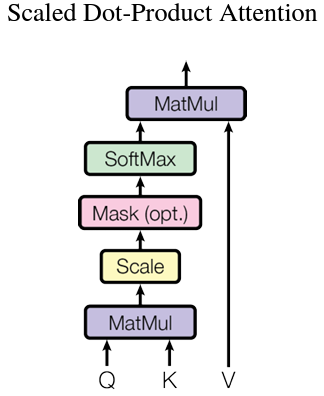
在实际情况中，我们往往会将数个向量 $q,k,v$ 分别打包成矩阵，也就是上图中的 $Q,K,V$，然后通过矩阵运算计算attention。公式如下
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^\text T}{ \sqrt{d_k}})V
$$

def attention(query, key, value, mask=None, dropout=None):
    """Compute 'Scaled Dot Product Attention'"""
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = scores.softmax(dim=-1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

Masking

注意到，上文中我们忽略了Scaled Dot-Product Attention中的 Mask(opt.) 这一部分，本节就会对此进行解释。

还是以日-英翻译作为例子，假设要将日语“kono eiga ga kirai”翻译到英语“I hate this movie”。当我们利用矩阵进行运算时，存在一个问题：我们希望每一步只用到当前已经获得的信息。比如在本例中，我们将“kono eiga ga kirai”翻译为了“I hate this movie”，翻译的流程是逐个语句进行的，比如我们在翻译 I 时，实际上我们只有 kono eiga ga kirai 的信息；同理，我们在翻译 hate 时，实际上只有 kono eiga ga kirai 和 I 的信息。但是我们在计算attention时可能将所有的向量打包了，因此就会导致模型的”视野”过大，而masking就是为了解决这一问题而提出的。

如图，我们可以将mask简单地理解为一个01矩阵，其中黑色块为1，白色块为0，将mask与原矩阵点乘即可。

为什么代码中写的是 scores = scores.masked_fill(mask == 0, -1e9)？

因为点乘mask之后还要经过softmax，而乘 1e-9 可以认为是将这个数字变成了 $-\inf$，经过softmax之后就变成了 $0$。

Multi-Head Attention

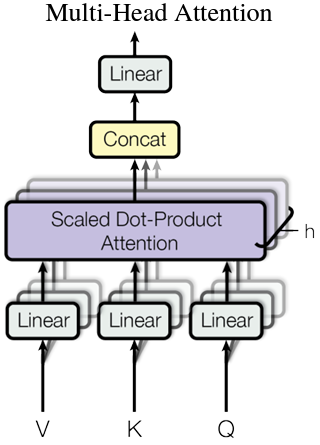
Multi-head Attention实际上就是将大矩阵切割成 $N$ 个大小相同的子矩阵然后分别求attention，最后再重新拼回一个大矩阵。

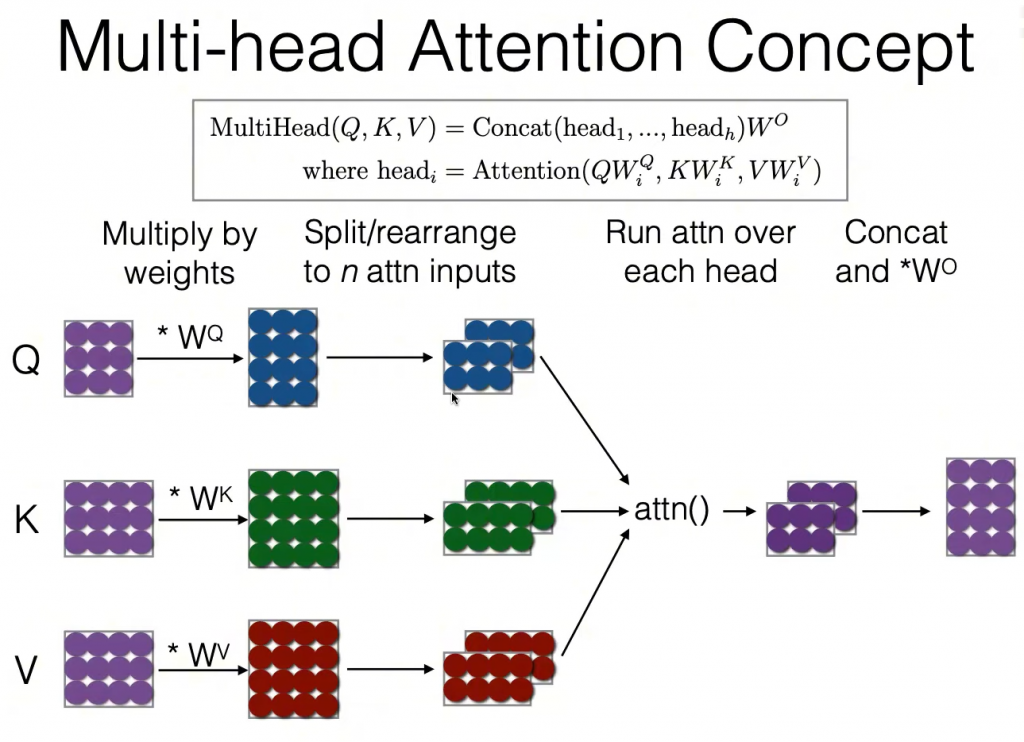
比如上图中，我们就展示了将大矩阵切分为2个小矩阵时的Multi-Head Self-Attention。

注意，transformer中一个单头注意力实际上在计算 $\text{softmax}(QW_i^Q \cdot (KW_i^K)^T / \sqrt{|K|}) VW_i^V$，我们聚焦于softmax中的内容，并不管缩放因子，则

$$
QW_i^Q \cdot (KW_i^K)^T = Q[W_i^Q \cdot(W_i^K)^T] K^T
$$

这实际上就是bilinear score function的转置，也就是说这两种方法一定程度上等价。

多头注意力使模型能够在不同的位置同时关注来自不同表示子空间的信息。使用单一注意力头时，平均会阻碍这一点。

举个例子，在翻译的情景下，我们不仅仅希望模型关注单词之间的对应关系，还希望模型能提取上下文联系，语法结构等联系。但是这些信息可能不能在单一空间中被全部表示出来，我们认为不同信息在不同子空间下会表现出不同特征，因此采用多头注意力机制。

再来理解一下论文中给出的公式（可以和上图找到对应关系）

$$
\begin{aligned} \text{MultiHead}(Q, K, V) &= \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \\ \text{where } \text{head}_i& = \text{Attention}(Q W_i^Q, K W_i^K, V W_i^V) \end{aligned}
$$

这里，$W_i^Q\in\mathbb R^{d_{\text{model}}\times d_k}, W_i^K\in\mathbb R^{d_{\text{model}}\times d_k}, W_i^V\in\mathbb R^{d_{\text{model}}\times d_v}，W^O\in\mathbb R^{hd_v\times d_{\text{model}}}$。

在原论文中，作者采用了 $h=8$ 个并行的注意力层（或者说heads），参数设置为 $d_k=d_v=d_{\text{model}}/h=64$。由于每个头的维度减少，总计算成本与全维度的单头注意力相似。

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        """Take in model size and number of heads."""
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = [
            lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
            for lin, x in zip(self.linears, (query, key, value))
        ]

        # 2) Apply attention on all the projected vectors in batch.
        x, self.attn = attention(
            query, key, value, mask=mask, dropout=self.dropout
        )

        # 3) "Concat" using a view and apply a final linear.
        x = (
            x.transpose(1, 2)
            .contiguous()
            .view(nbatches, -1, self.h * self.d_k)
        )
        del query
        del key
        del value
        return self.linears[-1](x)

代码中 self.linears = clones(nn.Linear(d_model, d_model), 4) 实际上声明了 $4$ 个线性层（全连接层），前三个就是 $W_i^Q,W_i^K,W_i^V$，用于对输入的 $Q,K,V$ 进行映射；最后一个则是 $W^O$。

Position-wise Feed-Forward Networks

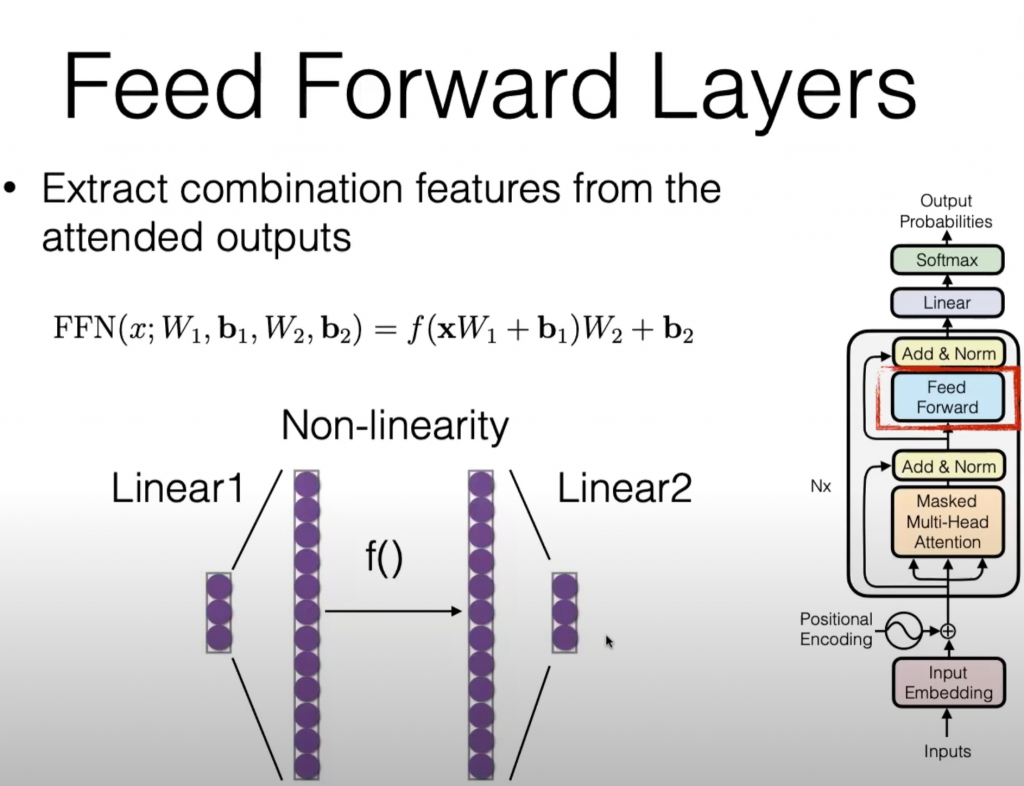
除了注意力子层之外，我们的编码器和解码器中的每个层都包含一个完全连接的前馈网络，该网络单独且相同地应用于每个位置。这由两个线性变换组成，中间有一个 ReLU。

class PositionwiseFeedForward(nn.Module):
    """Implements FFN equation."""

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(self.w_1(x).relu()))

这是一个非常简单的结构，由线性层1、激活函数（非线性变换）、线性层2构成。根据原文的参数设置 d_model = 512, d_ff = 2048。写成公式就是
$$
FFN(x) = \max (0, xW_1+b_1)W_2+b_2
$$
这个公式假设激活函数 $f$ 和原文一致，为ReLU。

Positional Encoding

由于我们的模型不包含递归和卷积，为了使模型能够利用序列的顺序，我们必须加入一些有关序列中tokens的相对或绝对位置的信息。

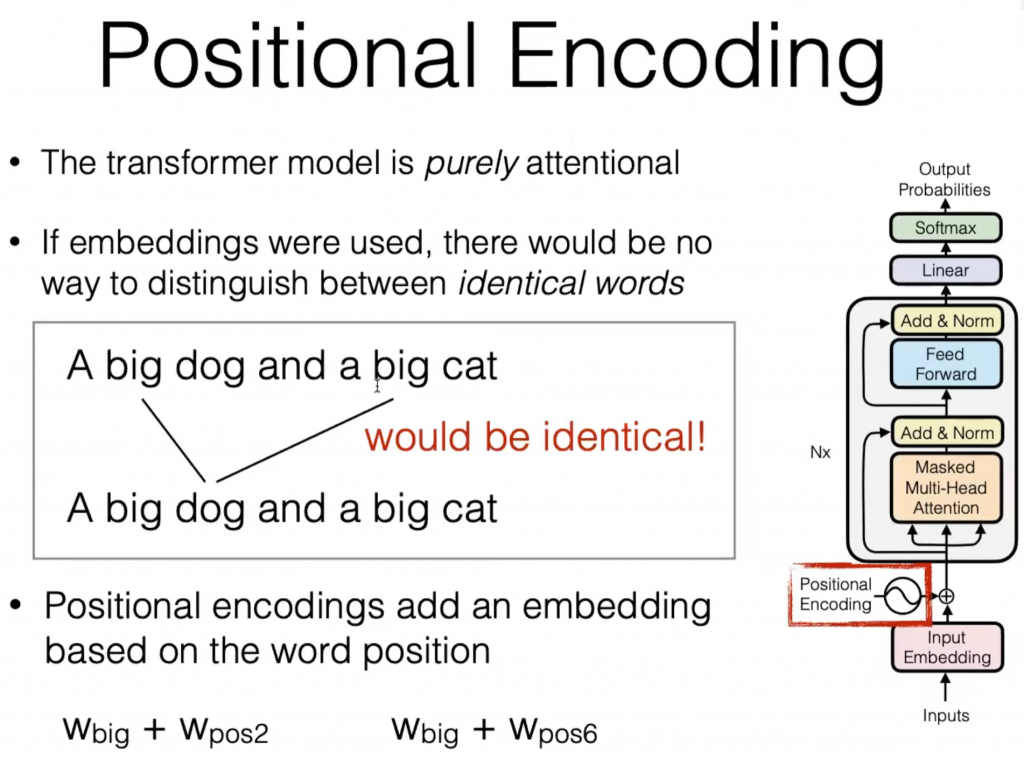
如图，对于这样一个语句 A big dog and a big cat，如果我们直接对于所有token进行映射，那么语句中的两个 big 就会是相同的vector，但是我们知道这两个 big 实际上修饰了不同的目标，尽管语义接近，但是肯定有所不同。因此我们需要加入token所在位置的信息，这样就能区分出不同位置相同单词的语义了。

在这项工作中，我们使用不同频率的正弦和余弦函数：
$$
PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right) \
PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)
$$
这里 $pos$ 表示位置（position），$i$ 表示维度。

class PositionalEncoding(nn.Module):
    """Implement the PE function."""

    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer("pe", pe)

    def forward(self, x):
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        return self.dropout(x)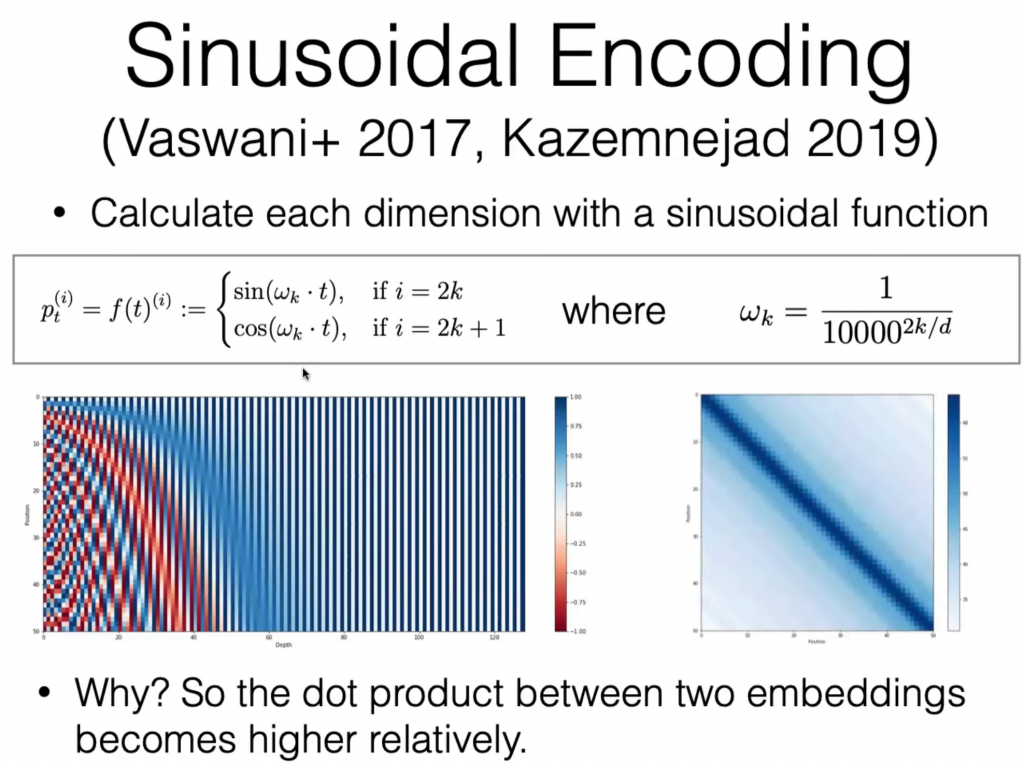

使用三角函数进行编码的一个直观理解在于：我们希望增加相似向量点乘的大小，减小不相似向量点乘的大小。所以采用三角函数，令向量点乘大小的衰减逐渐加速（如图）。

Bonus: Other Encodings

除了transformer原始论文中采用的sinusoidal encoding，我们还可以采用可学习的encoding，也就是将positional encoding作为一个参数加入模型，同时参与梯度的反向传播。

disavantage的解释：正弦和余弦的函数形式是周期性的，能够自然地对更长的序列（超出训练中见过的长度）进行编码，而学习式编码通常只对训练中见过的序列长度有效，无法很好地推广到更长的序列。

另一个比较sota的方法是RoPE，核心思路是我们更应该关注两个向量在原序列中的相对位置，并非绝对位置。

Encoder and Decoder Stacks

Encoder

Transformer Encoder由 $N=6$ 个相同的层堆叠而成

def clones(module, N):
    """Produce N identical layers."""
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

class Encoder(nn.Module):
    """Core encoder is a stack of N layers"""

    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, mask):
        """Pass the input (and mask) through each layer in turn."""
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

每层有两个主要的子层。第一个是多头自注意力机制（multi-head self-attention mechanism），第二个是简单的位置级全连接前馈网络（Position-Wise Fully Connected Feed-Forward Network，简称 FFN）。

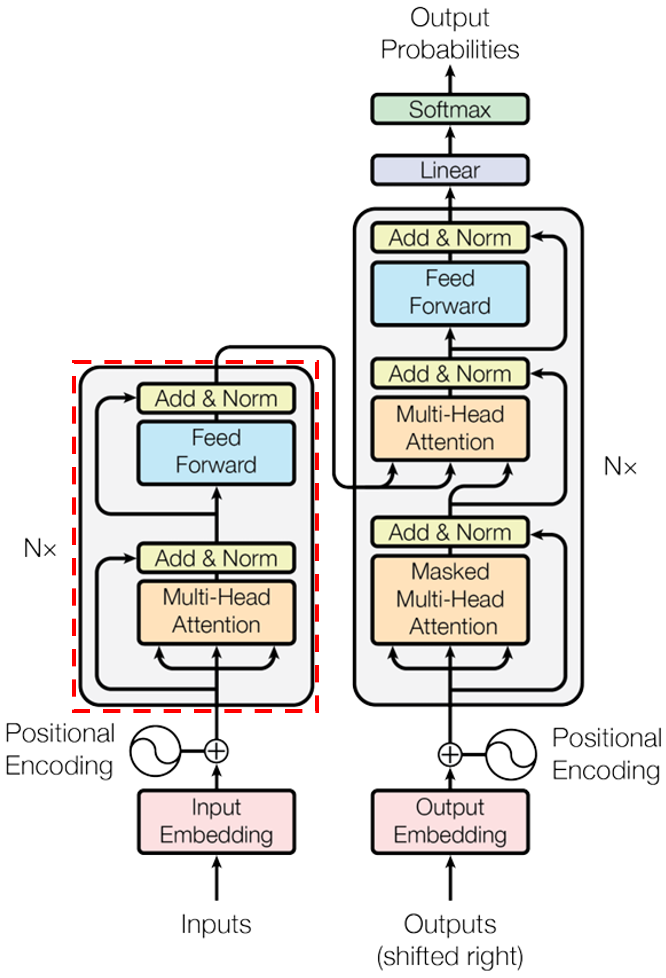
class EncoderLayer(nn.Module):
    """Encoder is made up of self-attn and feed forward (defined below)"""

    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        """Follow Figure 1 (left) for connections."""
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

这里任意两个子层之间都采用了残差连接（residual connections），并在此之后采用layer normalization(cite)。

class LayerNorm(nn.Module):
    """Construct a layernorm module (See citation for details)."""

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2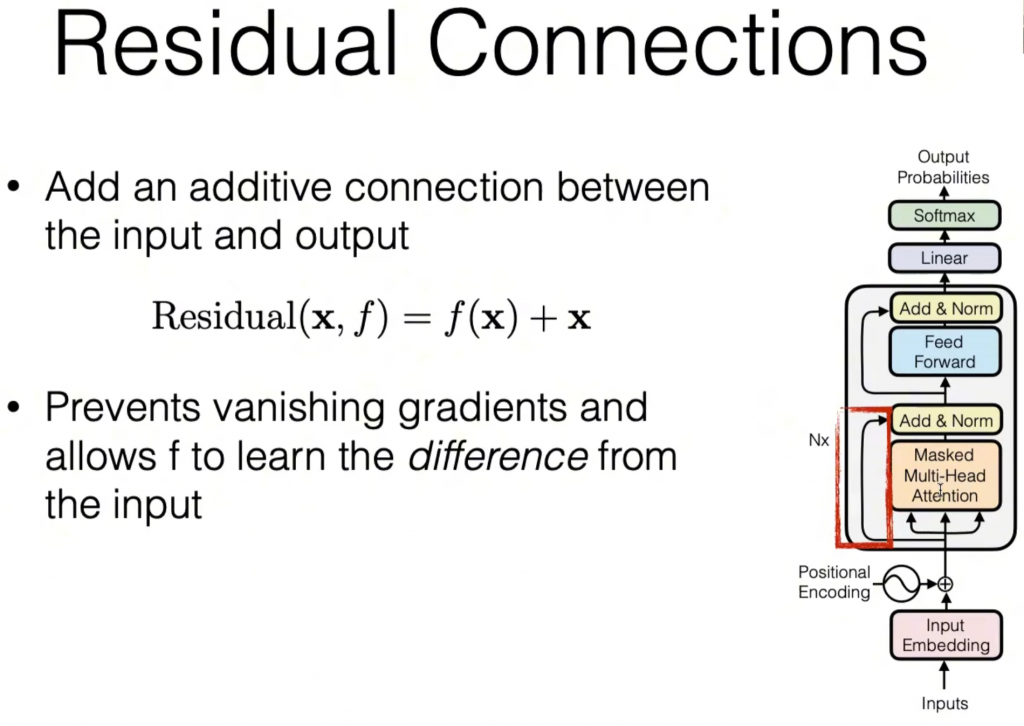

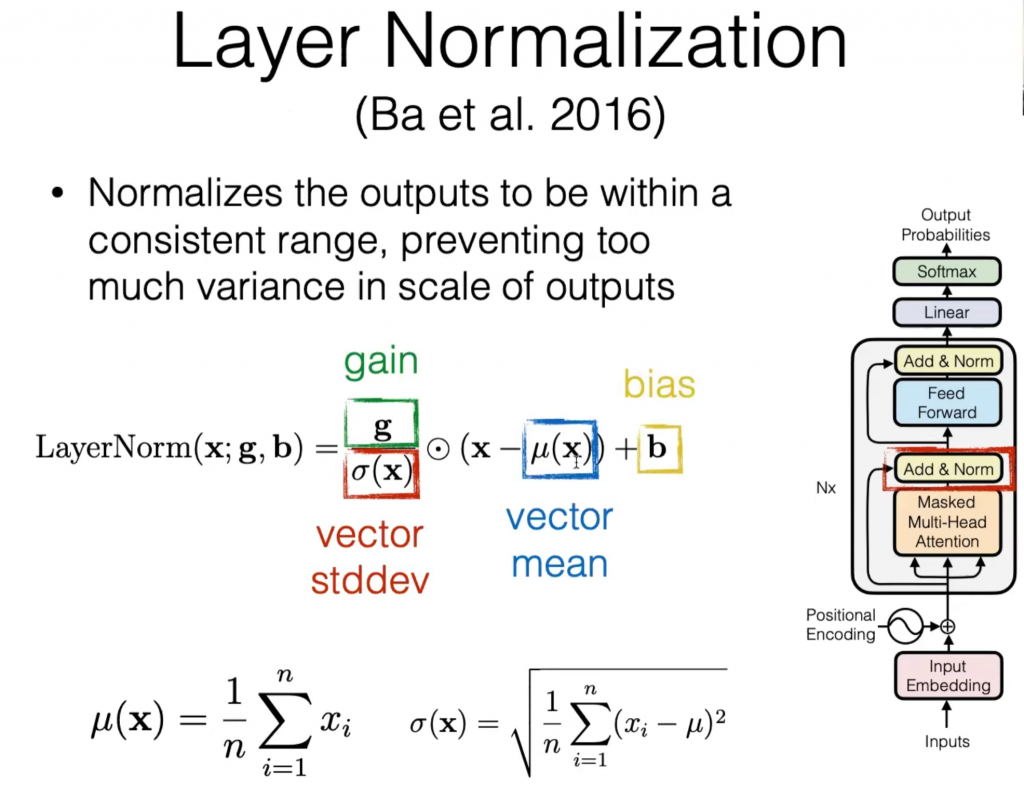
于是每个子层的输出实际上是 $\text{LayerNorm}(x+\text{SubLayer(x)})$。此外，我们还将 dropout(cite)应用于每个子层的输出，然后将其添加到子层输入并进行归一化。

class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

Bonus: Post- vs. Pre- Layer Norm

如果你仔细看了上方的代码实现，你会发现 x + self.dropout(sublayer(self.norm(x))) 和原始论文中的 $\text{LayerNorm}(x+\text{SubLayer(x)})$ 有一些不同，这就是本节的内容。

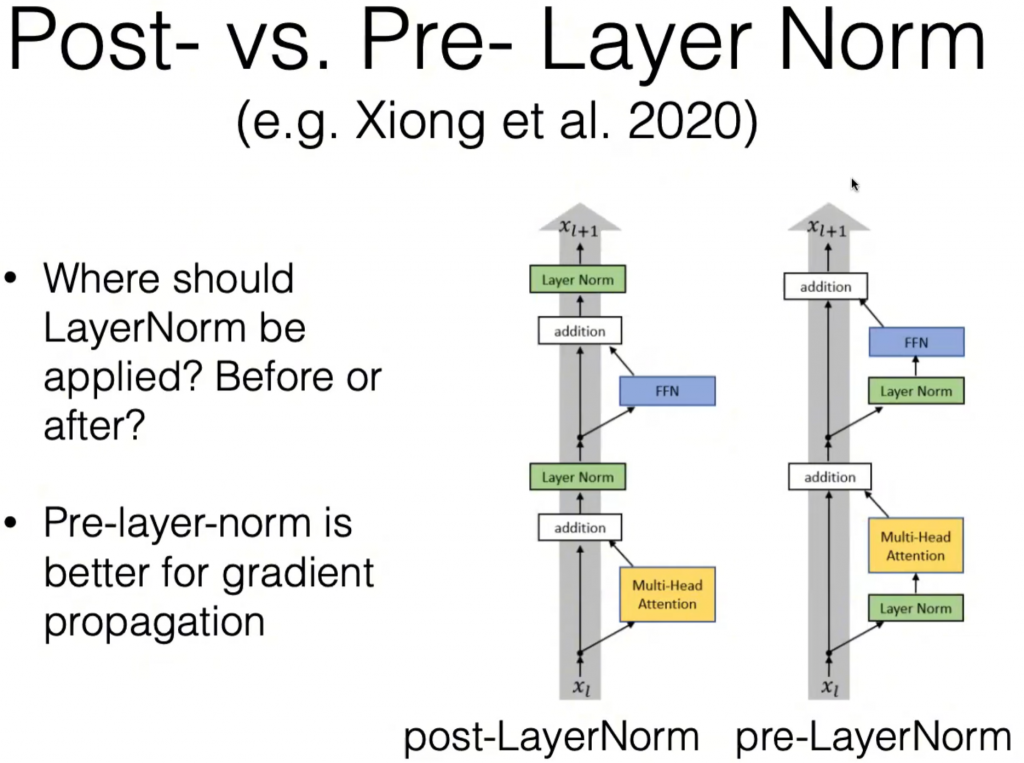
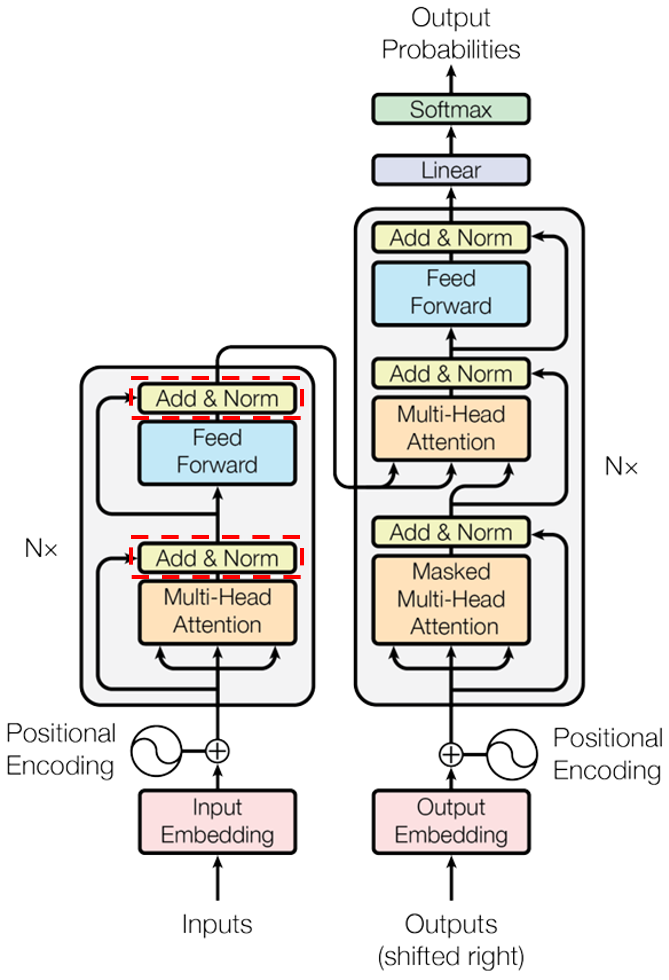
如图，Layer Norm应该在哪里被添加？transformer原始论文的做法是左边的Post-Layer Norm，但是实践表明右边的Pre-Layer Norm更优。

Pre-Layer Norm更适合梯度的反向传播，因为Post-Layer Norm会在网络的主干上做归一化，但是Pre-Layer Norm只会在残差连接处做归一化，并不会极大地影响网络主干回传的梯度。

Decoder

Transformer Decoder同样由 $N=6$ 个相同的层堆叠而成

class Decoder(nn.Module):
    """Generic N layer decoder with masking."""

    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

一个显著的不同之处在于：Decoder Layer中包含了两个attention层，其中Masked Multi-Head Attention层和encoder中的Multi-Head Attention层类似，都是self-attention，只不过加入了mask来屏蔽那么模型应当未知的信息。而decoder中的Multi-Head Attention层则变成了cross-attention，用于将encoder的输出和decoder的预测进行融合。

class DecoderLayer(nn.Module):
    """Decoder is made of self-attn, src-attn, and feed forward (defined below)"""

    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)

    def forward(self, x, memory, src_mask, tgt_mask):
        """Follow Figure 1 (right) for connections."""
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

def subsequent_mask(size):
    """Mask out subsequent positions."""
    attn_shape = (1, size, size)
    subsequent_mask = torch.triu(torch.ones(attn_shape), diagonal=1).type(
        torch.uint8
    )
    return subsequent_mask == 0

此外的结构都是类似的，包括在任意子层之间的残差连接+Layer Norm。

Embeddings

与其他的序列转换模型类似，transformer也采用可学习的token将输入tokens转换为维度为 d_model 的向量。此外还乘了一个缩放系数 $\sqrt{d_k}$。

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

这里 nn.Embedding 的核心功能是将离散的索引（如单词、字符或其他类别的整数索引）映射为连续的低维向量（嵌入向量）。例如，nn.Embedding(num_embeddings=1000, embedding_dim=64) 会创建一个形状为 $1000 \times 64$ 的嵌入矩阵。

观察模型结构不难发现，transformer输入需要两个embedding，对于翻译任务，input embedding表示源语言的词嵌入表示，output embedding表示目标语言的词嵌入表示。

Full Model

def make_model(
    src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1
):
    """Helper: Construct a model from hyperparameters."""
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab),
    )

    # This was important from their code.
    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform_(p)
    return model

接下来的代码是对该模型的测试：

def inference_test():
    test_model = make_model(11, 11, 2)
    test_model.eval()
    src = torch.LongTensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
    src_mask = torch.ones(1, 1, 10)

    memory = test_model.encode(src, src_mask)
    ys = torch.zeros(1, 1).type_as(src)

    for i in range(9):
        out = test_model.decode(
            memory, src_mask, ys, subsequent_mask(ys.size(1)).type_as(src.data)
        )
        prob = test_model.generator(out[:, -1])
        _, next_word = torch.max(prob, dim=1)
        next_word = next_word.data[0]
        ys = torch.cat(
            [ys, torch.empty(1, 1).type_as(src.data).fill_(next_word)], dim=1
        )

    print("Example Untrained Model Prediction:", ys)


def run_tests():
    for _ in range(10):
        inference_test()


def show_example(fn, args=None):
    if args is None:
        args = []
    if __name__ == "__main__":
        return fn(*args)


show_example(run_tests)

运行结果为

Example Untrained Model Prediction: tensor([[ 0, 10,  4,  0,  4,  0,  4,  0,  4,  0]])
Example Untrained Model Prediction: tensor([[0, 7, 9, 7, 9, 7, 9, 7, 9, 7]])
Example Untrained Model Prediction: tensor([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
Example Untrained Model Prediction: tensor([[0, 3, 3, 4, 8, 6, 7, 9, 2, 3]])
Example Untrained Model Prediction: tensor([[0, 4, 2, 7, 5, 4, 7, 5, 4, 7]])
Example Untrained Model Prediction: tensor([[0, 9, 0, 9, 0, 9, 0, 9, 0, 9]])
Example Untrained Model Prediction: tensor([[0, 5, 4, 5, 4, 5, 4, 5, 4, 5]])
Example Untrained Model Prediction: tensor([[0, 2, 7, 0, 2, 7, 0, 2, 2, 2]])
Example Untrained Model Prediction: tensor([[0, 6, 5, 6, 5, 8, 6, 5, 8, 6]])
Example Untrained Model Prediction: tensor([[ 0, 10,  9,  3, 10,  9,  3, 10,  9,  3]])

注意这里的初始化是随机的，所以运行结果不一定相同。