直线
定义
一般式
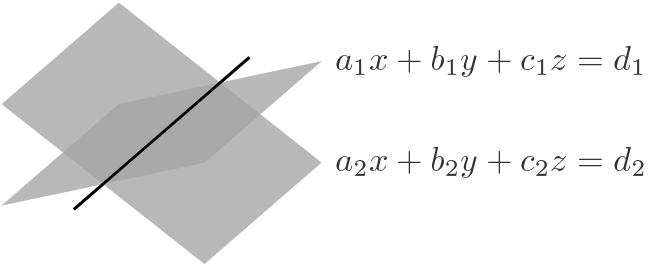
不像二维几何中,直线 $l$ 可以直接用一个方程 $ax+by=c$ 简单地表示,三维几何中 $ax+by+cz=d$ 表示一个平面。而直线可以表示为两个平面的交,即方程组
$$
l:\begin{cases}
\Pi_1: a_1x+b_1y+c_1z=d_1\\
\Pi_2: a_2x+b_2y+c_2z=d_2\\
\end{cases}
$$
点向式
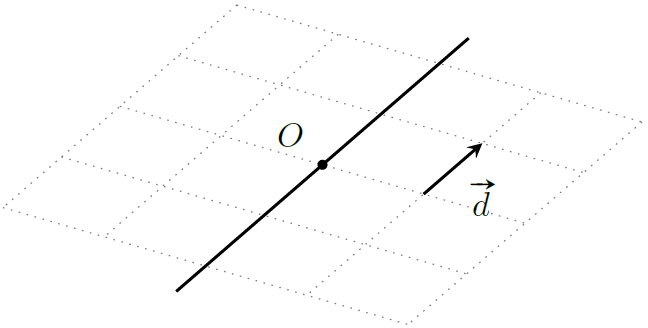
跟二维几何类似的是,一条直线也可以由直线上一点 $O$ 和直线的方向向量 $\boldsymbol d$ 表示
$$
l:O + t\boldsymbol d
$$
这里 $t$ 是参数方程中的参数,可以取任意实数。相较于一般式,点向式是三维直线更简洁、更直观的表示方法。
一般式转换为点向式
因为直线 $l$ 既在平面 $\Pi_1$ 上,又在平面 $\Pi_2$ 上,所以直线 $l$ 的方向向量 $\boldsymbol d$ 同时垂直于两平面的法向量 $\boldsymbol n_1,\boldsymbol n_2$,所以有 $\boldsymbol d = \boldsymbol n_1\times \boldsymbol n_2$。
然后,我们就只需要找到直线 $l$ 上任意一点 $O$ 的坐标。这里,我们将计算出 $l$ 上最接近原点的一点,公式如下
$$
O = \frac{(d_1\boldsymbol n_2 – d_2\boldsymbol n_1)\times \boldsymbol d}{|\boldsymbol d|^2}
$$
我们来分析一下这个公式,该式由两个向量相减得到,
$$
\begin{aligned}
\boldsymbol v_1 &= \frac{d_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\\
\boldsymbol v_2 &= \frac{d_2}{|\boldsymbol d|^2}(\boldsymbol n_1\times\boldsymbol d)\\
\end{aligned}
$$
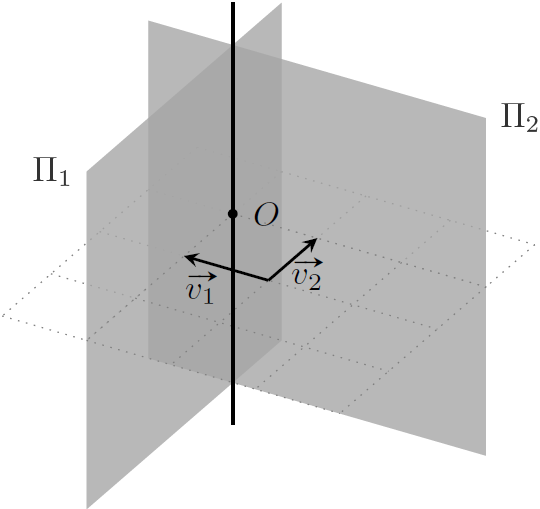
显然,$\boldsymbol v_1$ 是垂直于 $\boldsymbol n_2$(平行于 $\Pi_2$)的向量,$\boldsymbol v_2$ 是垂直于 $\boldsymbol n_1$(平行于 $\Pi_1$)的向量。因此,$\boldsymbol v_1$ 可以被视作是从原点出发,以平行于 $\Pi_2$ 的方向指向平面 $\Pi_1$ 的向量;$v_2$ 则是从原点出发,以平行于 $\Pi_1$ 的方向指向平面 $\Pi_2$ 的向量。
然后,我们验证点 $O$ 在平面 $\Pi_1$ 上
$$
\begin{aligned} \boldsymbol n_1\cdot O &= \boldsymbol n_1\cdot(\boldsymbol v_1+\boldsymbol v_2)\\ &= \boldsymbol n_1\cdot\boldsymbol v_1\\ &= \frac{d_1\boldsymbol n_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\\ &= \frac{d_1\boldsymbol d}{|\boldsymbol d|^2}(\boldsymbol n_1\times\boldsymbol n_2)\quad(三重积性质)\\ &= \frac{d_1\boldsymbol d}{|\boldsymbol d|^2}\cdot\boldsymbol d\\ &=d_1 \end{aligned}
$$
同理可证明点 $O$ 也在平面 $\Pi_2$ 上。此外,还可证明 $\boldsymbol v_1\perp \boldsymbol d$
$$
\begin{aligned} \boldsymbol v_1\times\boldsymbol d &= \frac{d_1}{|\boldsymbol d|^2}(\boldsymbol n_2\times\boldsymbol d)\cdot \boldsymbol d\\ &= \frac{d_1}{|\boldsymbol d|^2}\boldsymbol n_2\cdot(\boldsymbol d\times\boldsymbol d)\\ &= \boldsymbol 0 \end{aligned}
$$
同理可证明 $\boldsymbol v_2\perp\boldsymbol d$,于是点 $O$ 是直线 $l$ 上距离原点最近的一点。
点和直线
位置关系
假设我们需要验证某一点 $P$ 是否位于直线 $l:O+t\boldsymbol d$ 上,实际上只需要证明 $\vec{OP}$ 平行于 $\boldsymbol d$,也就是 $\boldsymbol d\times\vec{OP}=\boldsymbol 0$。
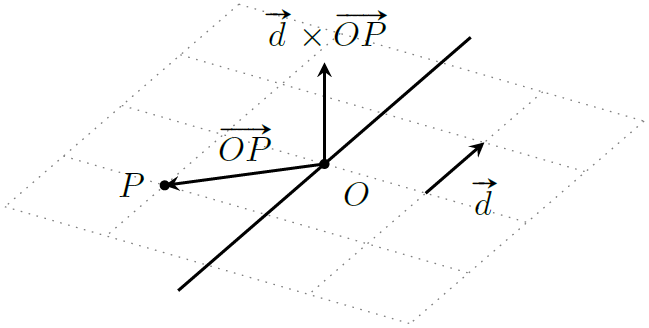
此外,$\boldsymbol d\times\vec{OP}$ 还可以用于计算点 $P$ 到直线 $l$ 的距离(叉积的绝对值等于平行四边形面积)
$$
\text{dist}_l P = \frac{|\boldsymbol d\times\vec{OP}|}{|\boldsymbol d|}
$$
投影点/反射点
如下图,作点 $P$ 关于直线 $l$ 的投影点 $P^\prime$。
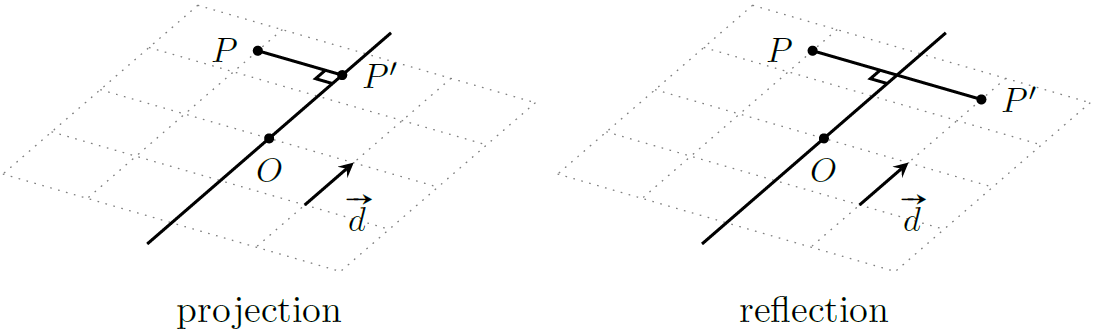
根据点积的性质有 $\vec{OP}\cdot \frac{\boldsymbol d}{|\boldsymbol d|}=|OP^\prime|$,所以
$$
\begin{aligned} \text{proj}_lP &= O + |OP^\prime|\cdot \frac{\boldsymbol d}{|\boldsymbol d|}\\ &= O + \vec{OP}\cdot\frac{\boldsymbol d}{|\boldsymbol d|}\cdot\frac{\boldsymbol d}{|\boldsymbol d|}\\ &= O + \frac{\vec{OP}\cdot \boldsymbol d\cdot\boldsymbol d}{|\boldsymbol d|^2} \end{aligned}
$$
反射点 $\text{refl}_lP$ 可以通过投影点求出
$$
\text{refl}_lP = P + 2(\text{proj}_lP-P)
$$
平面和直线
位置关系
设平面 $\Pi:\boldsymbol n\cdot P=d$,直线 $l:O+t\boldsymbol d$。如果平面 $\Pi$ 上某一点 $P$ 同时也是直线 $l$ 上一点,则有
$$
\boldsymbol n\cdot(O+t\boldsymbol d) = d
$$
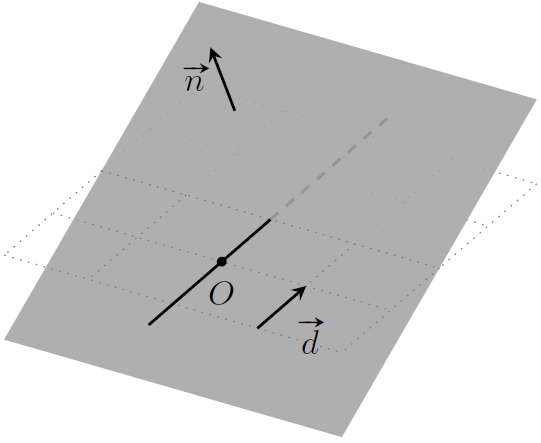
然后解出参数 $t$
$$
t = \frac{d-\boldsymbol n\cdot O}{\boldsymbol n\cdot\boldsymbol d} = \frac{-\text{side}_\Pi O}{\boldsymbol n\cdot\boldsymbol d}
$$
因此直线与平面的交点就是
$$
O + t\boldsymbol d = O – \frac{\text{side}_\Pi O}{\boldsymbol n\cdot\boldsymbol d}\cdot\boldsymbol d
$$
除了直线与平面相交的情况,直线还有可能平行于平面,此时直线的方向向量必然垂直于平面的法向量,即
$$
\boldsymbol d \cdot\boldsymbol n = 0
$$
投影直线/反射直线
线面角
类似于二面角,直线 $l$ 和平面 $\Pi$ 的线面角实际上就是方向向量 $\boldsymbol d$ 和法向量 $\boldsymbol n$ 之间的夹角 $\theta$。
根据余弦定理有
$$
\theta = \arccos(\frac{\boldsymbol n\cdot\boldsymbol d}{|\boldsymbol n||\boldsymbol d|})
$$
此外,$\theta$ 的范围一般也是取 $[0,\frac{\pi}{2}]$。
线线角
两条直线之间的夹角实际上就是由两条直线的方向向量定义的,计算类似于线面角或二面角。
直线和直线
直线与直线之间可能有以下三种情况:
- 平行
- 相交
- 偏离
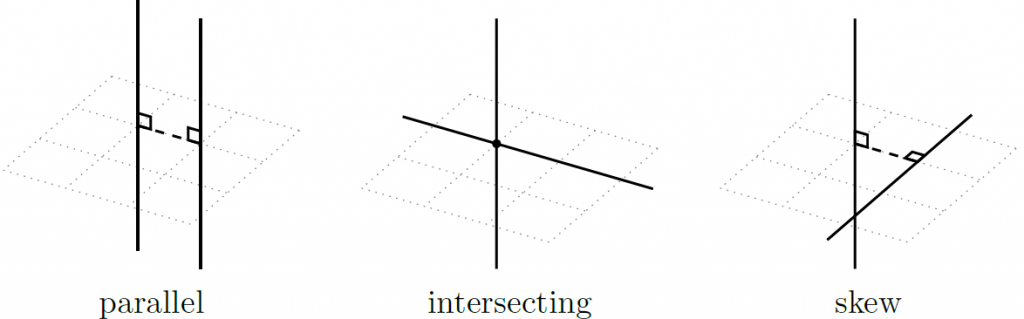
下文中,我们将讨论两直线 $l_1:O_1+k\boldsymbol d_1$ 和 $l_2:O_2+t\boldsymbol d_2$ 之间的关系。
平行
首先,两直线平行是最简单的一种情况,只需要判断两条直线之间的方向向量是否平行,即
$$
\boldsymbol d_1\times \boldsymbol d_2 = \boldsymbol 0
$$
如果两直线平行,则它们之间的距离就是点 $O_1$ 到直线 $l_2$ 的距离。
非平行
设点 $C_1$ 是直线 $l_1$ 上最接近直线 $l_2$ 的点,点 $C_2$ 是直线 $l_2$ 上最接近直线 $l_1$ 的点,那么线段 $C_1C_2$ 必然同时垂直于 $l_1,l_2$,且 $|C_1C_2|$ 就是两直线之间的最短距离。设 $\boldsymbol n = \boldsymbol d_1\times \boldsymbol d_2$,因为向量 $\vec{C_1C_2}$ 同时垂直于 $\boldsymbol d_1,\boldsymbol d_2$,所以 $\vec{C_1C_2}\parallel \boldsymbol n$,于是
$$
\text{dist}_{l_1}l_2 = |C_1C_2| = \frac{|\vec{C_1C_2}\cdot\boldsymbol n|}{|\boldsymbol n|}
$$
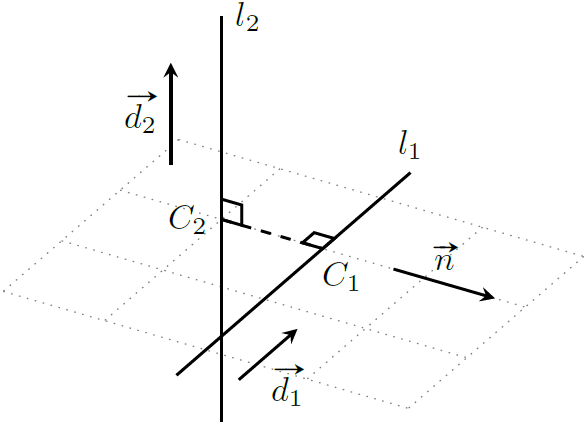
但是我们还不知道 $C_1,C_2$ 的坐标,无法求解上式,因此我们需要将问题进一步转化:考虑到点积的性质(向量之间的投影不变,则向量点积的值不变),$\vec{C_1C_2}\cdot \boldsymbol n$ 式中可以将点 $C_2$ 移动至直线 $l_2$ 上任意一点 $C_2^\prime$ 而不影响该式的值,即 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{C_1C_2^\prime}\cdot \boldsymbol n$。为了方便起见,我们取点 $C_2^\prime = O_2$,即 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{C_1O_2}\cdot \boldsymbol n$。同理点 $C_1$ 也可以移动至直线 $l_1$ 上任意一点 $C_1^\prime$,取点 $C_1^\prime=O_1$,于是 $\vec{C_1C_2}\cdot \boldsymbol n = \vec{O_1O_2}\cdot \boldsymbol n$,
$$
\text{dist}_{l_1}l_2 = \frac{|\vec{O_1O_2}\cdot\boldsymbol n|}{|\boldsymbol n|}
$$
实际上点 $C_1,C_2$ 的坐标也是可以求的:设直线 $l_2$ 和向量 $\boldsymbol n$ 张开的平面为 $\Pi_2$,此时点 $C_1$ 实际上就是平面 $\Pi_2$ 和直线 $l_1$ 之间的交点。
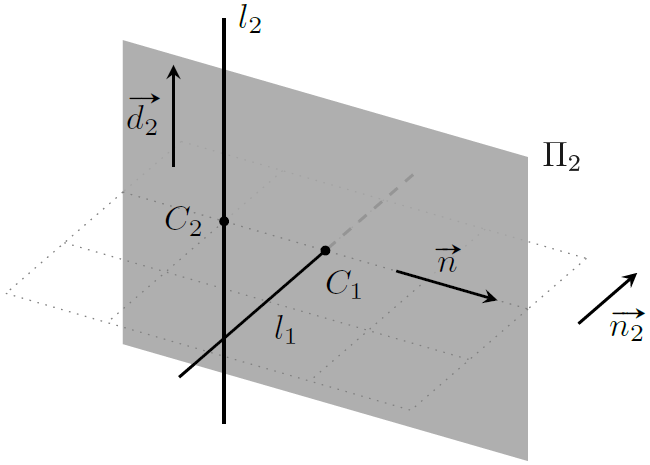
即 $\Pi_2$ 的法向量为 $\boldsymbol n_2 = \boldsymbol d_2\times\boldsymbol n$,利用直线平面之间的距离公式即可求出
$$
C_1 = O_1 + \frac{\vec{O_1O_2}\cdot\boldsymbol n_2}{\boldsymbol d_1\cdot\boldsymbol n_2}\cdot\boldsymbol d_1
$$
特别地,当 $l_1,l_2$ 相交时,$C_1,C_2$ 是同一个点($l_1,l_2$ 的交点)。
记 $\vec w = Q(y) – P(x),\vec{p}=\vec{AB},\vec q=\vec{CD}$,如果 $|\vec w|$ 取最小值,则 $\vec w$ 在最理想情况下应该同时垂直于 $\vec {AB},\vec{CD}$,也就是满足方程 $\vec w\cdot\vec{p}=\vec 0, \vec w\cdot\vec{q}=\vec 0$,这实际上是一个二元一次方程组
$$
\begin{cases}
(C + y\cdot\vec{q} – A – x\cdot \vec{p})\cdot \vec{p}=\vec 0\\
(C + y\cdot\vec{q} – A – x\cdot \vec{p})\cdot \vec{q}=\vec 0\\
\end{cases}\Rightarrow
\begin{cases}
\vec p\cdot\vec p\cdot x – \vec p\cdot\vec q\cdot y = (C-A)\cdot \vec{p}\\
\vec p\cdot\vec q\cdot x – \vec q\cdot\vec q\cdot y = (C-A)\cdot \vec{q}\\
\end{cases}
$$
解出该方程即可。
线段
点和线段
要求点 $P$ 到线段 $AB$ 的最短距离,实际上就是判断点 $P$ 到直线 $AB$ 的投影点 $H$ 是否位于线段 $AB$ 内。如果是,则最短距离就是 $|PH|$;如果不是,则最短距离就是 $\min(|PA|, |PB|)$。
此外,也可以通过直接求点 $P$ 到线段 $AB$ 的最近点得到答案,先求出点 $P$ 到直线 $AB$ 的投影点 $H$,然后求出 $t = (\vec{AH}\cdot \vec{AB}) / (\vec{AB}\cdot\vec{AB})$,然后将 $t$ clamp到区间 $[0,1]$ 内,则 $A+t\cdot \vec{AB}$ 就是点 $P$ 到线段 $AB$ 的最近点。
线段和线段
三维空间中,线段 $AB$ 和 $CD$ 之间的最短距离是一个相对复杂的问题,但实际上也有非常漂亮的解决办法,下面介绍的方法来源于这里。
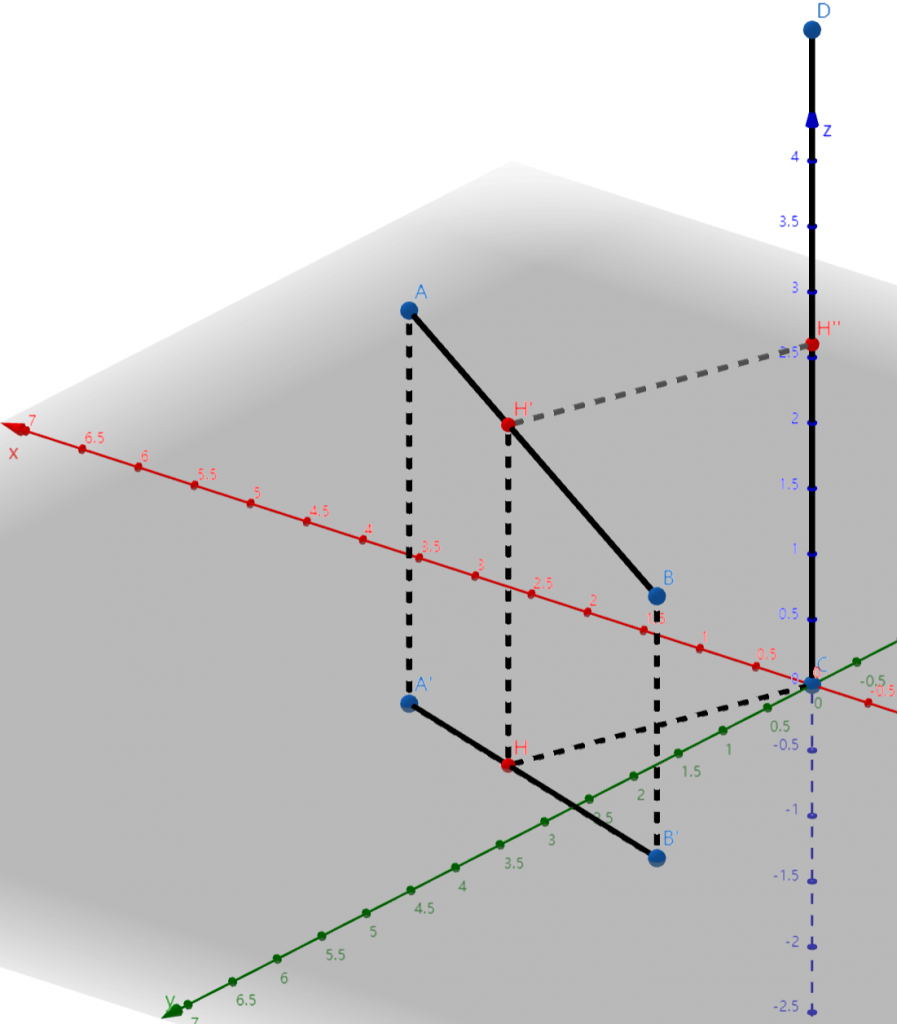
如图,我们先构建一个由法向量 $\vec{CD}$ 和点 $C$ 定义的平面 $\Pi$(上图中的 $xOy$ 平面),然后将线段 $AB$ 投影到该平面上,投影线段为 $A^\prime B^\prime$。找到点 $C$ 到线段 $A^\prime B^\prime$ 的最近点 $H$,再作 $HH^\prime \parallel AA^\prime$。
此时,线段 $AB$ 和 $CD$ 之间的最短距离就是点 $H^\prime$ 到线段 $CD$ 的最短距离(图中的 $|H^\prime H^{\prime\prime}|$)。这个方法的核心思路是:如果我们沿着 $\vec{DC}$ 方向从上向下看,那么线段 $AB$ 和 $CD$ 之间的最短距离就被转化为了点 $C$ 到线段 $AB$ 之间的距离(因为此时线段 $CD$ 退化为了一个点)。
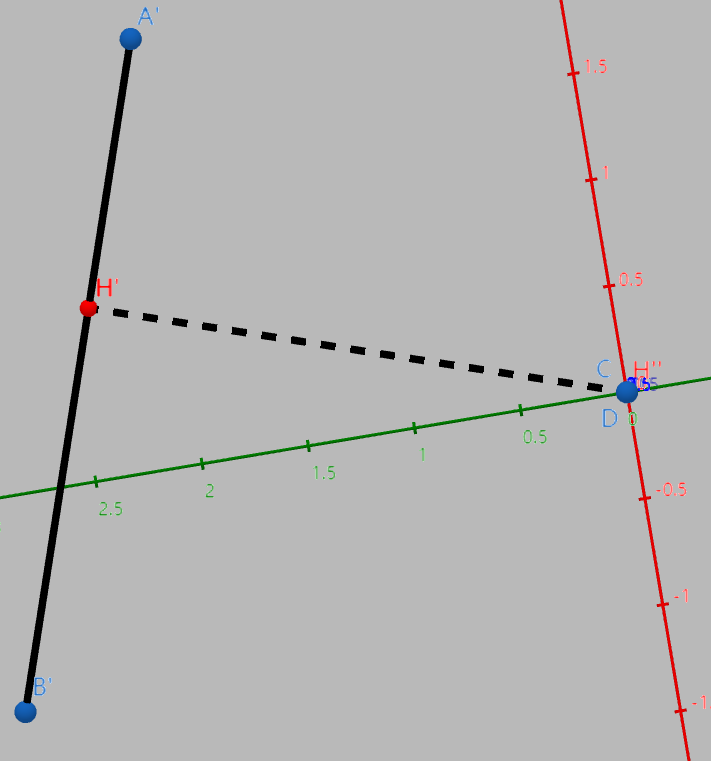
当然,你也可以用前文提到的计算直线之间最近点对,然后判断点对是否分别在线段上进行计算。