三维几何2. 平面 – st1vdy's blog

平面

定义

平面是满足方程 $ax+by+cz=d$ 的点 $(x,y,z)$ 的集合。类似于二维平面（直线），这里 $a,b,c$ 定义了平面的方向，$d$ 定义了平面相对于原点的偏移量。

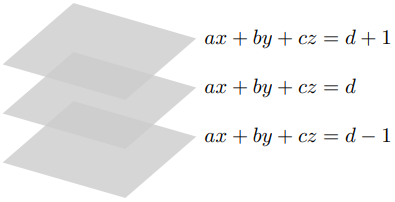
法向量 $\boldsymbol n=(a,b,c)$ 是一个垂直于平面 $ax+by+cz=d$ 的向量，因此常用于描述平面的方向。

关于法向量的补充

假设平面 $\Pi:ax+by+cz=d$ 上有一点 $P_0(x_0,y_0,z_0)$，平面上任意一点 $P(x,y,z)$ 与点 $P_0$ 构成的向量都应该垂直于法向量 $\boldsymbol n$，也就是点积为零
$$
\begin{aligned}
\boldsymbol n\cdot \vec{P_0P} &= (a,b,c)\cdot(x-x_0,y-y_0,z-z_0) \\
&= ax+by+cz – (ax_0+by_0+cz_0)
\end{aligned}
$$
又因为点 $P_0$ 是平面 $\Pi$ 上的点，所以满足方程 $\Pi:ax_0+by_0+cz_0=d$，因此
$$
\boldsymbol n\cdot \vec{P_0P} = ax+by+cz – (ax_0+by_0+cz_0) = 0
$$

除了法向量垂直于平面上任意向量这一定义，我们还可以这样思考：假设点 $P(x,y,z)$ 是平面 $\Pi:ax+by+cz=d$ 上的任意一点，则向量 $\vec{OP}$ 与法向量 $\boldsymbol n$ 的点积恒为 $d$。

根据以上讨论可知，定义一个平面实际上需要四个量 $(a,b,c,d)$，其中 $(a,b,c)$ 是该平面的法向量 $\boldsymbol n$，而 $d$ 是一个偏移量，因此实际上就是两个量：$\boldsymbol n, d$。

根据给定条件构建一个平面

给定直线方程 $ax+by+cz=d$。
给定平面上一个点 $P(x,y,z)$ 和平面法向量 $\boldsymbol n(a,b,c)$ 这种情况实际上只需要求出 $d$，根据平面方程可知 $ax+by+cz=d$，因此 $d=\boldsymbol n \cdot P$。
给定平面上的三个点 $P,Q,R$ 定义向量 $\boldsymbol u = \vec{PQ},\boldsymbol v = \vec{PR}$，则法向量 $\boldsymbol n=\boldsymbol u\times\boldsymbol v$，$d = \boldsymbol n\cdot P$。

点和平面

位置关系

判断点 $P$ 和平面 $\Pi(ax+by+cz=d)$ 的位置关系，只需要判断 $\boldsymbol n\cdot P – d$ 的正负

$\boldsymbol n\cdot P – d\gt 0$：点 $P$ 在平面 $\Pi$ 的上方
$\boldsymbol n\cdot P – d= 0$：点 $P$ 在平面 $\Pi$ 上
$\boldsymbol n\cdot P – d\lt 0$：点 $P$ 在平面 $\Pi$ 的下方

此外，$\boldsymbol n\cdot P – d$ 可以用于表示点到平面的有向距离。

点到平面的距离

设 $Q$ 是平面 $\Pi$ 上任意一点，作 $PH\perp \boldsymbol n$，则点 $P$ 到平面 $\Pi$ 的距离就是 $|QH|$。
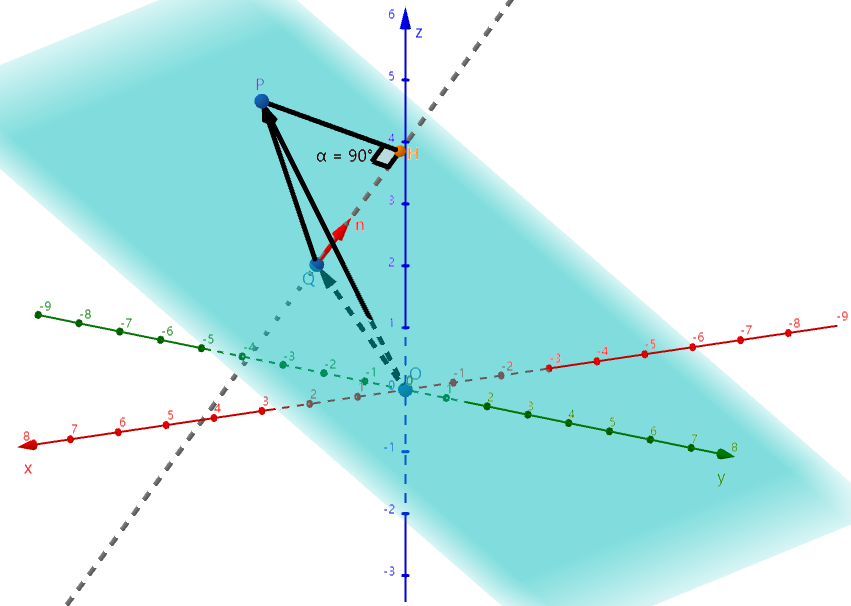
根据点积的几何意义可知 $\vec{QP}\cdot \boldsymbol n = |\vec{QP}||\boldsymbol n|\cos\angle PQH$，若法向量 $\boldsymbol n$ 是单位法向量，则 $\vec{QP}\cdot \boldsymbol n = |\vec{QP}|\cos\angle PQH = |QH|$。根据向量的特性：$\vec{QP}=\vec{OP}-\vec{OQ}$，结合法向量证明章节中的性质：$\boldsymbol n\cdot \vec{OQ}=d$，推出
$$
\begin{aligned}
\vec{QP}\cdot \boldsymbol n &= (\vec{OP}-\vec{OQ})\cdot \boldsymbol n\\
&= \boldsymbol n\cdot P – d
\end{aligned}
$$
如果 $\boldsymbol n$ 不是单位法向量，则还要除以 $\boldsymbol n$ 的模长：$\text{dist}_\Pi P = \frac{|\boldsymbol n\cdot P – d|}{|\boldsymbol n|}$，你可能对它的展开式很熟悉：
$$
\frac{|\boldsymbol n\cdot P – d|}{|\boldsymbol n|} = \frac{|ax+by+cz-d|}{\sqrt{a^2+b^2+c^2}}
$$

记 $\text{side}_\Pi P = \boldsymbol n\cdot P – d$。

投影点/反射点

我们在上一节中已经求出了点 $P$ 到平面 $\Pi$ 的有向距离 $\text{side}_\Pi P = \boldsymbol n\cdot P – d$，利用该性质即可直接求出投影点

$$
\begin{aligned}
\text{proj}_\Pi P &= P + \vec{HQ}\\ &= P – \text{side}_\Pi P\cdot \frac{\boldsymbol n}{|\boldsymbol n|} \\
\end{aligned}
$$

反射点就是 $P+2\vec{HQ} = P – 2\cdot\text{side}_\Pi P\cdot \frac{\boldsymbol n}{|\boldsymbol n|}$。

平面平移

假设平面 $\Pi$ 沿向量 $\boldsymbol t$ 的方向平移 $|\boldsymbol t|$ 个单位，因为平面法向量 $\boldsymbol n$ 不会因平移发生变化，所以只有偏移量 $d$ 改变。

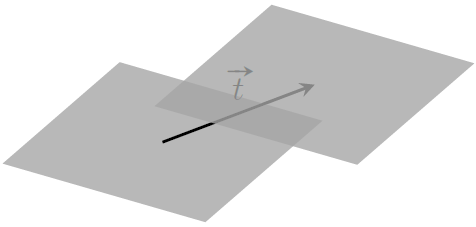
设 $P$ 是平面 $\Pi$ 上任意一点，则有 $\boldsymbol n\cdot P = d$。同时设平移后的平面为 $\Pi^\prime:ax+by+cz=d^\prime$，则
$$
d^\prime = \boldsymbol n\cdot(P + \boldsymbol t) = d + \boldsymbol n\cdot\boldsymbol t
$$
特殊地，如果要沿着法向量 $\boldsymbol n$ 的方向将平面平移 $\delta$ 个单位距离，此时 $\boldsymbol t = \frac{\delta\boldsymbol n}{|\boldsymbol n|}$，于是
$$
d^\prime = d + \boldsymbol n\cdot \frac{\delta\boldsymbol n}{|\boldsymbol n|} = d + \delta |\boldsymbol n|
$$

二面角

求两平面 $\Pi_1:\boldsymbol n_1\cdot P=d_1,\Pi_2:\boldsymbol n_2\cdot P=d_2$ 之间的夹角，实际上等价于求法向量 $\boldsymbol n_1,\boldsymbol n_2$ 之间的夹角。

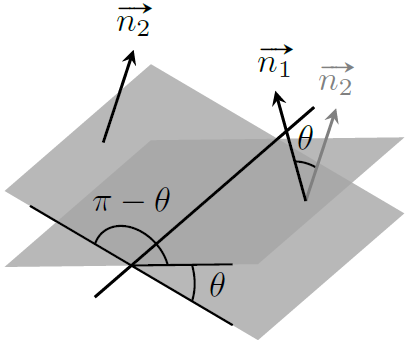
设向量 $\boldsymbol n_1,\boldsymbol n_2$ 之间的夹角为 $\theta$，根据余弦定理有
$$
\cos\theta = \frac{\boldsymbol n_1\cdot\boldsymbol n_2}{|\boldsymbol n_1||\boldsymbol n_2|}\Rightarrow \theta = \arccos(\frac{\boldsymbol n_1\cdot\boldsymbol n_2}{|\boldsymbol n_1||\boldsymbol n_2|})
$$
由于二面角实际上有两个（除了垂直的情况，分别是一个锐角和一个钝角，相加为 $\pi$），我们一般认为较小的那个角度为二面角的角度，因此如果 $\theta\gt\frac{\pi}{2}$，则取 $\frac{\pi}{2}-\theta$ 作为二面角的角度。

平面

定义