B-splines – st1vdy's blog

B-spline

Cox-de Boor recursion formula

定义集合 $U$ 由 $m+1$ 个不降的实数 $u_0\le u_1\le\cdots\le u_m$ 构成，我们称 $u_i$ 为结点（knot），$U$ 为结点向量（knot vector）。

给定结点向量 $U$，则其对应的 $k$ 次B-spline $N_{i,k}(u),\ u\in[u_0,u_m]$ 就是由以下递推公式定义的多项式：

$$
\begin{aligned}
&N_{i,0}(u) = \begin{cases}
1 & u_i\le u\lt u_{i+1}\\
0 & \text{otherwise}
\end{cases}\\
&N_{i,k}(u) = \frac{u-u_i}{u_{i+k}-u_i}N_{i,k-1}(u) + \frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}N_{i+1,k-1}(u)
\end{aligned}
$$

这被称为是Cox-de Boor recursion formula。

Sample

B-spline的定义式看起来很复杂，但是仔细分析就会发现它实际上就是一个关于自变量 $u$ 的函数，只不过用了递归式来定义。递归的边界是 $N_{i,0}(u)$，这是一个只能为0或1的分段函数。

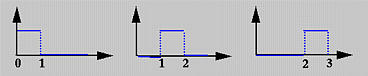
比如 $u_0=0,u_1=1,u_2=2,u_3=3$，则

$$
\begin{aligned}
N_{0,0}(u) &= \begin{cases}
1 & 0\le u\lt 1\\
0 & \text{otherwise}
\end{cases}\\
N_{1,0}(u) &= \begin{cases}
1 & 1\le u\lt 2\\
0 & \text{otherwise}
\end{cases}\\
N_{2,0}(u) &= \begin{cases}
1 & 2\le u\lt 3\\
0 & \text{otherwise}
\end{cases}\\
\end{aligned}
$$

下图为 $N_{0,0},N_{1,0},N_{2,0}$ 的图像：

为了更直观地理解 $N_{i,k}(u)$ 的递推，我们画出递归的树状图：

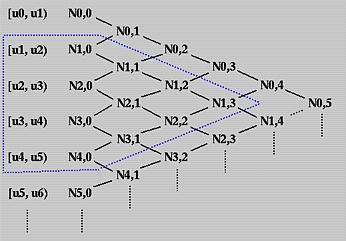
为了计算 $N_{i,1}$，需要先计算出 $N_{i,0},N_{i+1,0}$，然后就能再计算 $N_{i,2}$……

还是以 $u_0=0,u_1=1,u_2=2,u_3=3$ 为例，我们计算 $N_{i,1}(u)$：

$$
\begin{aligned}
N_{0,1}(u) &= \frac{u-u_0}{u_{1}-u_{0}}N_{0,0}(u) + \frac{u_{2}-u}{u_{2}-u_{1}}N_{1,0}(u)\\
&= uN_{0,0}(u) + (2-u)N_{1,0}(u)\\
&= \begin{cases}
u & 0\le u\lt 1\\
2 – u & 1\le u\lt 2
\end{cases}\\
N_{1,1}(u) &= \frac{u-u_1}{u_2-u_1}N_{1,0}(u) + \frac{u_3-u}{u_3-u_1}N_{2,0}(u)\\
&= uN_{1,0}(u) + (3-u)N_{2,0}(u)\\
&= \begin{cases}
u & 1\le u\lt 2\\
3-u & 2\le u\lt 3
\end{cases}
\end{aligned}
$$

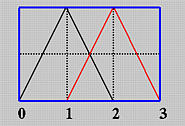
下图为 $N_{0,1},N_{1,1}$ 的图像：

再计算 $N_{0,2}$：

$$
\begin{aligned}
N_{0,2}(u) &= \frac{u-u_0}{u_2-u_0}N_{0,1}(u) + \frac{u_3-u}{u_3-u_1}N_{1,1}(u)\\
&= 0.5u N_{0,1}(u) + 0.5(3-u)N_{1,1}(u)\\
&= \begin{cases}
0.5u^2 & 0\le u\lt 1\\
0.5u(2-u) + 0.5u(3-u) & 1\le u\lt 2\\
0.5(3-u)^2 & 2\le u\lt 3
\end{cases}
\end{aligned}
$$

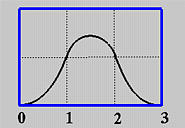
下图为 $N_{0,2}$ 的图像：

Two Important Observations

Observation1

观察树状图，$N_{i,k}(u)$ 的递归边界必然是 $N_{i,0}(u),N_{i+1,0}(u),\cdots,N_{i+k,0}(u)$，也就是说 $N_{i,k}(u)$ 只在 $[u_i,u_{i+k+1})$ 上非零；或者更进一步地， $N_{i,k}(u)$ 是 $N_{i,0}(u),N_{i+1,0}(u),\cdots,N_{i+k,0}(u)$ 的线性组合。

Observation2

反向思考 $N_{i,0}(u)$ 可以影响哪些 $N_{i,k}(u)$，我们可以画出上图中的三角形区域。不难发现 $N_{i,0}(u)$ 对于 $k$ 次B-spline至多可以影响 $N_{i-k,k}(u), N_{i-k+1,k}(u),\cdots,N_{i,k}(u)$。

Meaning of the Coefficients

最后，我们研究递推式 $N_{i,k}(u) = \frac{u-u_i}{u_{i+k}-u_i}N_{i,k-1}(u) + \frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}N_{i+1,k-1}(u)$ 中系数的意义，根据上方的观察可知 $N_{i,k-1}(u)$ 在 $[u_i,u_{i+k})$ 上非零，$N_{i+1,k-1}$ 在 $[u_{i+1},u_{i+k+1})$ 上非零。系数 $\frac{u-u_i}{u_{i+k}-u_i}$ 表示 $u$ 到左端点 $u_i$ 的长度占 $N_{i,k-1}(u)$ 非零区间 $[u_i,u_{i+k})$ 的比例，系数 $\frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}$ 表示 $u$ 到右端点 $u_{i+k+1}$ 的长度占 $N_{i+1,k-1}(u)$ 非零区间 $[u_{i+1},u_{i+k+1})$ 的比例，如下图：

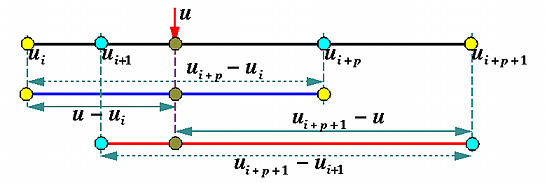
*图里的 $p$ 等价于文章中的 $k$。

也就是说 $N_{i,k}(u)$ 实际上就是 $N_{i,k-1}(u)$ 和 $N_{i+1,k-1}(u)$ 的线性组合。

Properties

$N_{i,k}(u)$ 是一个关于 $u$ 的 $k$ 次多项式。这一点通过上方的树形图递推过程很容易证明。
$N_{i,k}(u)\ge 0$。
$N_{i,k}(u)$ 仅在区间 $[u_i,u_{i+k+1})$ 上非零（对应上方观察1）。
在区间 $[u_i,u_{i+1})$ 上，至多 $k+1$ 个 $k$ 次多项式非零：$N_{i-k,k},N_{i-k+1,k},\cdots,N_{i,k}\neq0$（对应上方观察2）。
$1$ 的分割（Partition of unity）：在区间 $[u_i,u_{i+1})$ 上，至多 $k+1$ 个 $k$ 次多项式非零：$N_{i-k,k},N_{i-k+1,k},\cdots,N_{i,k}\neq0$，且这些多项式之和为 $1$，即
$$
\sum_{j=i-k}^i N_{j,k}(u) = 1,\quad u\in[u_i,u_{i+1})
$$
证明如下：
1. 首先，对于 $k=0$ 有 $N_{i,0}(u) = \begin{cases}1 & u\in[u_i,u_{i+1})\\ 0 & \text{otherwise}\end{cases}$，性质成立。
2. 假设 $k\lt p$ 时，$\sum_{j=i-k}^i N_{j,k}(u) = 1,\quad u\in[u_i,u_{i+1})$ 均成立，于是有 $N_{i-p+1,p-1}(u) + \cdots + N_{i,p-1}(u)=1$。
3. $k=p$ 时，
$$
\begin{aligned}
N_{i-p,p}(u)+N_{i-p+1,p}(u)+\cdots+N_{i,p}(u) =&\ \frac{u-u_{i-p}}{u_{i}-u_{i-p}}N_{i-p,p-1}(u) + \frac{u_{i+1}-u}{u_{i+1}-u_{i-p+1}}N_{i-p+1,p-1}(u)+\\
&\ \frac{u-u_{i-p+1}}{u_{i+1}-u_{i-p+1}}N_{i-p+1,p-1}(u) + \frac{u_{i+2}-u}{u_{i+2}-u_{i-p+2}}N_{i-p+2,p-1}(u)+\\
&\ \cdots+\\
&\ \frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u) + \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\\
=&\ \frac{u-u_{i-p}}{u_{i}-u_{i-p}}N_{i-p,p-1}(u) + [N_{i-p+1,p-1}(u) + \cdots + N_{i,p-1}(u)] + \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\\
=&\ \frac{u-u_{i-p}}{u_{i}-u_{i-p}}N_{i-p,p-1}(u) + \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u) + 1\\
=&\ 1
\end{aligned}
$$
对于一个 $k$ 次的B-spline，在一个重数为 $p$ 的结点（即 $u_i=u_{i+1}=\cdots=u_{i+p-1}$）处，该函数的光滑性是 $C^{k-p}$（即 $k-p$ 阶连续可导）。
比如上文中的 $N_{0,2}(u) = \begin{cases}0.5u^2 & 0\le u\lt 1\\0.5u(2-u) + 0.5u(3-u) & 1\le u\lt 2\\0.5(3-u)^2 & 2\le u\lt 3\end{cases}$ 就是 $C^1$ 光滑（一阶连续可导）。
证明参考论文B(asic)-Spline Basics.。

B-spline Curves

B-spline Curves Definition

给定 $n+1$ 个控制点（control points） $P_0,P_1,\cdots,P_{n}$ 和 $n+k+1$ 个结点构成的结点向量 $U = (u_0,u_1,\cdots,u_{n+k})$，就能定义一条 $k$ 次B-spline曲线：

$$
S(u) = \sum_{i=0}^n N_{i,k}(u) P_i
$$

在B-spline curve中，结点向量的选取一般有以下几种特殊形式：

uniform：$u_{i+1}-u_i$ 是常数，比如 $U=(0,1,2,3,4)$。
open uniform：前 $k+1$ 和后 $k+1$ 个 $u_i$ 分别相等，其余 $u_i$ 则满足 $u_{i+1}-u_i$ 是常数，比如 $U=(0,0,0,0,1,2,3,4,4,4,4)$。这个trick也被称为是”clamped”，这也将是我们后文中主要讨论的B-spline curve的构造形式。

Properties

性质1

B-spline curve $S(u)$ 是由 $n+1$ 条 $k$ 次分段曲线构成的，这就是 $N_{i,k}(u)$ 的性质。

性质2

用open uniform形式结点向量构造的B-spline curve的起点、终点分别是 $P_0$ 和 $P_n$。注意到 $N_{0,k}(u)$ 是控制点 $P_0$ 的系数，并且在 $[u_0,u_{k+1})$ 上非零，因为 $u_0=u_1=\cdots=u_k$，所以 $N_{0,0}(u),N_{1,0}(u),\cdots,N_{k-1,0}(u)=0$，只有 $N_{k,0}\neq 0$，因此 $N_{k,0}=1$，即 $S(u_0)=P_0$，同理有 $S(u_{n+k})=P_1$。（这也是open uniform的核心优势）

性质3

可以用低阶曲线去近似大量的控制点

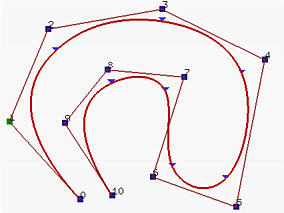
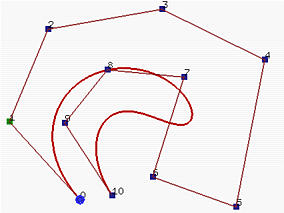
上图中的B-spline curve由11个控制点，14个结点构成，由定义可知该曲线为3次曲线，而同样情况下的Bezier curve因为次数过高所以近似效果劣于B-spline curve。

性质4

修改控制点 $P_i$ 只会影响区间 $[u_i,u_{i+p+1})$ 上的曲线 $S(u)$。

这是因为控制点 $P_i$ 的系数是 $N_{i,k}(u)$，而 $N_{i,k}(u)$ 仅在区间 $[u_i,u_{i+p+1})$ 上非零。

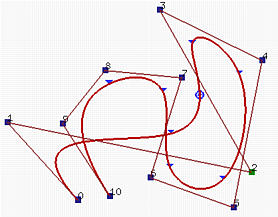
如上图，移动 $P_2$ 只会影响局部的曲线。

性质5

假设 $u\in [u_{i},u_{i+1})$，则 $S(u)$ 位于控制点构成的凸包 $P_{i-k},P_{i-k+1},\cdots,P_{i}$ 内部。

因为 $u\in [u_{i},u_{i+1})$，该区间对应的B-spline $N_{i,0}$ 只能影响到 $N_{i,k}(u),\cdots,N_{i-p+1}(u),N_{i-p}(u)$，它们分别是控制点 $P_i,\cdots,P_{i-k+1},P_{i-k}$ 的系数，这些系数全部非零且和为 $1$，因此 $S(u)$ 必然位于凸包 $P_{i-k},P_{i-k+1},\cdots,P_{i}$ 内部（线性组合的性质）。

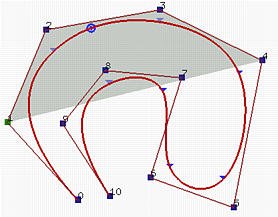
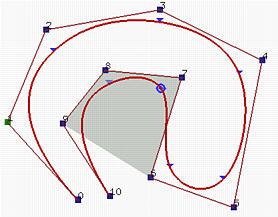
性质6

对于一个 $k$ 次的B-spline curve，如果其结点向量中没有重复点，那么该曲线的光滑性至少是 $C^{k-1}$。

性质7

对于一个 $k$ 次的B-spline curve，在一个重数为 $p$ 的结点（即 $u_i=u_{i+1}=\cdots=u_{i+p-1}$）处，该曲线的光滑性是 $C^{k-p}$（当结点向量中没有重复点时，$p=1$，该性质等价于性质6）。

这点通过B-spline的性质6即可推出。

性质8

Bezier curve是B-spline curve的特殊情况，假设 $n=k$（即B-spline的次数为 $n$，结点向量满足 $u_0=u_1=\cdots=u_k, u_{k+1}=u_{k+2}=\cdots=u_{n+k+1}$），（为了推导方便，我们假设 $u_0=0,u_{k+1}=1$），此时

$$
\begin{aligned}
N_{i,k}(u) &= \frac{u-u_i}{u_{i+k}-u_i}N_{i,k-1}(u) + \frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}N_{i+1,k-1}(u)\\
&= uN_{i,k-1}(u) + (1-u)N_{i+1,k-1}(u)
\end{aligned}
$$

这和Bezier curve中的bernstein多项式的递推式：$B_{i,n} = tB_{i,n-1}(t) + (1-t)B_{i+1,n-1}(t)$ 相同。

实际上Bezier curve在一般情况下就是由 $n-k+1$ 条Bezier Curve拼接而成的。

Code implementation

from typing import List, Tuple
import matplotlib.pyplot as plt
import numpy as np
import math


def bezier(p: List[Tuple[float, float]]):
    n = len(p) - 1
    x, y = [], []
    for t in np.linspace(0, 1, 1000):
        xt, yt = 0, 0
        for i in range(n + 1):
            xt += math.comb(n, i) * ((1 - t) ** (n - i)) * (t ** i) * p[i][0]
            yt += math.comb(n, i) * ((1 - t) ** (n - i)) * (t ** i) * p[i][1]
        x.append(xt)
        y.append(yt)

    plt.plot(x, y, label="bezier curve")
    xx, yy = zip(*p)
    plt.scatter(xx, yy)
    plt.plot(xx, yy, linestyle='dashed')
    plt.legend()
    plt.show()


def b_splines(p: List[Tuple[float, float]], t: List[float]):
    n = len(p) - 1
    k = len(t) - n - 2
    x, y = [], []

    for v in np.linspace(t[0], t[-1], 1000):
        dp = {}

        def cox_de_boor(i, k):
            if (i, k) in dp:
                return dp[(i, k)]
            if k == 0:
                dp[(i, k)] = 1 if t[i] <= v < t[i + 1] else 0
                return dp[(i, k)]
            else:
                c1 = (v - t[i]) / (t[i + k] - t[i]) if t[i + k] > t[i] else 0
                c2 = (t[i + k + 1] - v) / (t[i + k + 1] - t[i + 1]) if t[i + k + 1] > t[i + 1] else 0
                dp[(i, k)] = c1 * cox_de_boor(i, k - 1) + c2 * cox_de_boor(i + 1, k - 1)
                return dp[(i, k)]

        xt, yt = 0, 0
        for i in range(n + 1):
            n_ik = cox_de_boor(i, k)
            xt += n_ik * p[i][0]
            yt += n_ik * p[i][1]

        x.append(xt)
        y.append(yt)

    plt.plot(x[:-1], y[:-1], label="b-spline curve")
    xx, yy = zip(*p)
    plt.scatter(xx, yy)
    plt.plot(xx, yy, linestyle='dashed')
    plt.legend()
    plt.show()


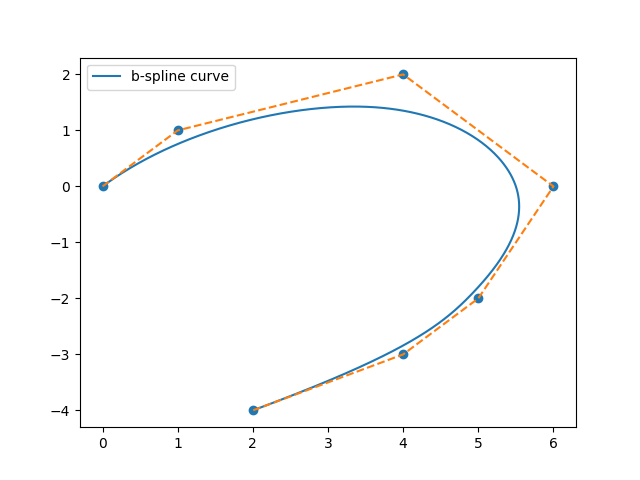
p = [(0, 0), (1, 1), (4, 2), (6, 0), (5, -2), (4, -3), (2, -4)]
t2 = [0, 0, 0, 1, 2, 3, 4, 5, 5, 5]
t3 = [0, 0, 0, 0, 1, 2, 3, 4, 4, 4, 4]
t6 = [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
# bezier(p)
b_splines(p, t3)

B-spline Curve的代码实现实际上就是实现Cox-de Boor recursion formula，写一个记忆化搜索即可。

References

B-spline Basis Functions: Definition. (n.d.). https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-basis.html
B-spline Curves: Important Properties. (n.d.). https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-curve-prop.html
Coolwater (https://math.stackexchange.com/users/84917/coolwater), B-Spline basis function partition of unity, URL (version: 2019-05-31): https://math.stackexchange.com/q/3246650
BoorCarl, D., & Center, W. U. M. M. R. (n.d.). B(asic)-Spline Basics. DTIC. https://apps.dtic.mil/sti/citations/ADA172773