背景

考研初试成绩刚出来，等待复试中……为了练习一下机试，正好和老友参加一下校赛，摇来了Hugin和Suzukaze。因为Hugin在北京，要了一个线上参赛的名额，队名沿用了去年省赛的队名。本以为大伙都已经是退役一年的废物了，没想到三人三机一通乱切就这样了：

部分题解

这里只放我知道做法的题目（有的题直接被队友秒了）。

B Puzzle: Guide Arrow

因为箭头边必选，所以先对所有的箭头边建图。建好的图 $G$ 必然是一个有向树森林 $F$，否则无解。

考虑题设条件，实际上等价于：每一条箭头边都必须指向构造出的生成树的根结点（特殊结点），因此我们只需要从森林 $F$ 中每一个出度为 $0$ 的结点开始向外搜索，并将搜索到的结点加入构造的生成树 $T$，这样就能保证每条箭头边一定指向根节点。最后我们再把剩下的结点加入 $T$，并检查构造是否合法。

C Puzzle: Shikaku

构造方案如下：

H Game: Bloons TD

一个比较恶心的几何，非常卡常。

翻译一下题意：给定一个 $n$ 个点的简单多边形 $S$，$q$ 次询问，每次询问给出二维平面上的一个点 $P$，询问：从点 $P$ 出发的所有射线中，与 $S$ 的交点个数为奇数/偶数的射线数量？如果是无限条就输出 oo。

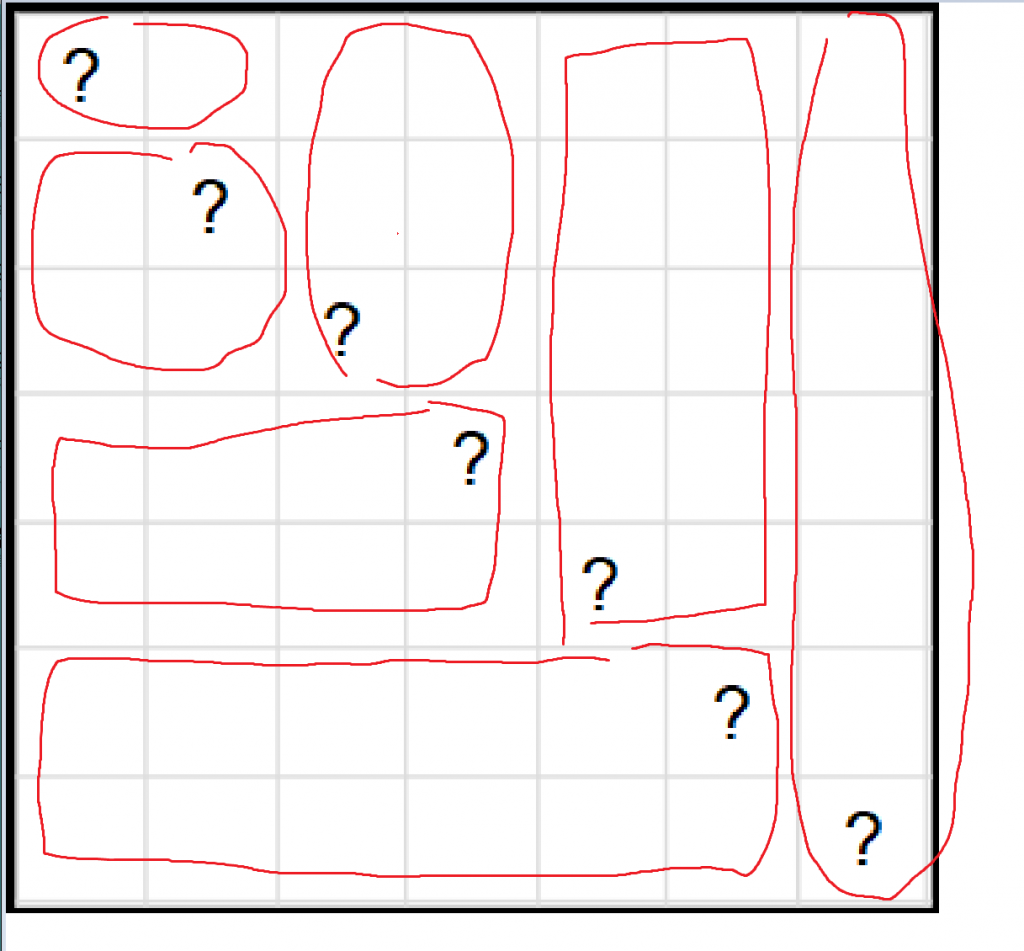
观察1：当点 $P$ 在 $S$ 内部时，交点数为奇数的射线有无穷多条；点 $P$ 在 $S$ 外部时，交点数为偶数的射线有无穷多条。

观察2：当且仅当这条射线经过简单多边形 $S$ 的至少一个顶点时，才会导致

1. 点 $P$ 在 $S$ 内部，交点数为偶数的射线
2. 点 $P$ 在 $S$ 外部，交点数为奇数的射线

如上图两条红色射线的情况。

然后就是本题的核心观察3：什么情况会导致观察2中的两种情况？注意上图中下方的红色射线 $NB$，这条射线与多边形有两个交点，导致奇偶性发生变化的那个特殊交点是点 $D$，这是因为与 $D$ 直接相邻的两个点 $C,E$ 在射线的同一侧，也就是说当射线通过点 $D$ 后这条射线仍然在多边形的内部，这就会导致交点个数的奇偶性发生变化（而点 $B$ 就不会导致奇偶性变化，因为射线通过点 $B$ 后就来到了多边形的外部）。

综上，对于每次询问，我们只需要枚举多边形的所有顶点，并统计所有共线且同方向的顶点中（比如上方例子中的 ${N,D,B}$；${M,G,I,K}$）有几个顶点不会造成“穿越”（也就是 $D$ 这种顶点），如果恰好有奇数个这类顶点就会导致奇偶性的变化。

最后是代码实现，首先必须先进行一个特判：判断询问的点是否在多边形的内部，利用ray casting或者winding number就可以做到 $O(n)$。然后就是枚举所有的共线且同方向的顶点，如果通过极角排序实现，那么复杂度就是 $O(n\log n)$，这会导致总复杂度为 $O(qn\log n)$，直接T飞（我比赛中就是这样死的）。

正确的姿势是哈希，因为题目中的一个条件：所询问的点与多边形的边不平行，所以对于多边形上的每个顶点 $S_i = (x_i,y_i)$ 和所询问的点 $P=(X,Y)$，我们只需要知道斜率 $\frac{Y-y_i}{X-x_i}$ 就能实现 $O(N)$ 的枚举。具体实现上可以这么做：取一个模数 $P$，然后 $\frac{Y-y_i}{X-x_i} = (Y-y_i)\cdot (X-x_i)^{-1}\pmod{P}$，只要这个 $P$ 取在 $O(N)$ 的量级，那么我们就可以预处理所有 $(X-x_i)^{-1}\pmod{P}$ 的逆元，然后拉链法哈希一下……非常卡常，我用邻接表模拟的拉链法cache裂了，换了ac-library里面学的Compressed Sparse Row才过的：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int MOD = (int)10103;
int iv[MOD], used[MOD], pre[MOD], nxt[MOD];
vector<int> start, elist;
int n, q;
void csr_init(const vector<pair<int, int>>& edges) {
    fill(start.begin(), start.end(), 0);
    fill(elist.begin(), elist.end(), 0);
    for (const auto& e : edges) {
        start[e.first + 1]++;
    }
    for (int i = 1; i <= MOD; i++) {
        start[i] += start[i - 1];
    }
    auto counter = start;
    for (const auto& e : edges) {
        elist[counter[e.first]++] = e.second;
    }
}
inline int normal(long long a) { return (a % MOD + MOD) % MOD; }
inline int mul(int a, int b) { return (int)((long long)a * b % MOD); }
int sign(ll k) {
    if (k > 0) return 1;
    else if (k < 0) return -1;
    return 0;
}

struct point {
    int x, y;
    point() {}
    point(int _x, int _y) :x(_x), y(_y) {}
    point operator + (const point& k) const { return point(k.x + x, k.y + y); }
    point operator - (const point& k) const { return point(x - k.x, y - k.y); }
    void input() { cin >> x >> y; }
};
using polygon = vector<point>;
ll dot(point k1, point k2) { return 1ll * k1.x * k2.x + 1ll * k1.y * k2.y; }
ll cross(point k1, point k2) { return 1ll * k1.x * k2.y - 1ll * k1.y * k2.x; }
bool windingNumber(const polygon& p, point q) {
    int res = 0;
    for (int i = 0; i < n; i++) {
        int j = nxt[i];
        bool below = (p[i].y < q.y);
        if (below != (p[j].y < q.y)) {
            int ccw = sign(cross(p[i] - q, p[j] - p[i]));
            if (below == (ccw > 0)) {
                res += (below ? 1 : -1);
            }
        }
    }
    return res == 0;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    iv[1] = 1;
    for (int i = 2; i < MOD; i++)
        iv[i] = mul(iv[MOD % i], (MOD - MOD / i));
    cin >> n >> q;
    start.resize(MOD + 1);
    elist.resize(MOD);
    vector<pair<int, int>> pr(n);
    vector<point> p(n);
    for (auto& i : p)
        i.input();
    for (int i = 0; i < n; i++) {
        pre[i] = (i - 1 + n) % n;
        nxt[i] = (i + 1) % n;
    }

    while (q--) {
        point k;
        k.input();
        fill(used, used + MOD, 0);
        int op = windingNumber(p, k);
        int ans_e = 0, ans_o = 0;
        for (int i = 0; i < n; i++) {
            p[i] = p[i] - k;
            pr[i] = { mul(normal(p[i].x), iv[normal(p[i].y)]) ,i };
        }
        csr_init(pr);

        auto calc = [&]() {
            int res = 0;
            for (int i = 0; i < MOD; i++) {
                if (start[i] == start[i + 1]) continue;
                int sp = 0, flag = 0, s = -1, ok = 1;
                for (int j = start[i]; j < start[i + 1]; j++) {
                    int& m = elist[j];
                    if (used[m])
                        continue;
                    if (!flag) {
                        flag = 1;
                        s = elist[j];
                    }
                    if (1ll * p[s].y * p[m].x == 1ll * p[s].x * p[m].y && dot(p[s], p[m]) > 0) {
                        used[m] = 1;
                        int l = pre[m], r = nxt[m];
                        int ccw1 = sign(cross(p[l], p[m]));
                        int ccw2 = sign(cross(p[r], p[m]));
                        sp ^= (ccw1 * ccw2 == 1);
                    } else {
                        ok = 0;
                    }
                }
                res += sp;
                if (!ok) i--;
            }
            return res;
        };

        if (op == 0) { // 点在内部
            cout << calc() << " " << "oo\n";
        } else { // 点在外部
            cout << "oo " << calc() << "\n";
        }
        for (int i = 0; i < n; i++)
            p[i] = p[i] + k;
    }
    return 0;
}

J Classic: CP test

先考虑 $k=1$ 时怎么做，显然就是一个最大子段和问题，然后发现题目中 $k\le 200$，因此直接冲了一发做 $k$ 次最大子段和的贪心就过了……

K Classic: N Real DNA Pots

二分答案 $K$，那么就有 $K\le \frac{y_j-y_i}{x_j-x_i}$，转换一下就是 $y_i-Kx_i \le y_j-Kx_j$，这就变成了一个LIS问题。