排序算法
|
711
|
0
|
总结

5354 字
|
60 分钟

本文假设需要排序的数组是 $A[]$，并且是不降序的排列 $(A[j]\ge A[i])_{j\gt i}$。

默认数组下标从 $0$ 开始。

插入排序

基础插入排序

一句话概括：从左往右遍历数组，将每次遍历到的元素 $A[i]$ 向左移动到可能的最左侧的位置 $j$，要求满足 $A[j+1]\gt A[j]$ 。（有点不严谨，但不影响理解）

void insertionSort(vector<int>& a) {
    int n = a.size();
    for (int i = 1; i < n; i++) {
        int key = a[i], j = i;
        while (j > 0 && key < a[j - 1]) {
            a[j] = a[j - 1];
            j--;
        }
        a[j] = key;
    }
}

插入排序性质

  • 空间复杂度：$O(1)$。（这里指的是额外需要的辅助空间，不包括原数组的 $O(N)$）
  • 时间复杂度：最优 $O(N)$，最劣 $O(N^2)$。平均情况下大概是 $\frac{N^2}{4}$，因此时间复杂度 $O(N^2)$。
  • 稳定性：大小相同的元素相对位置不改变，因此插入排序是稳定的排序算法。

折半插入排序

一句话概括：在插入排序中枚举到第 $i$ 位时，左侧的 $A[0],\ldots,A[i-1]$ 一定已经是有序序列了，因此我们可以直接二分查找 $A[i]$ 应该插入的位置。

我的评价：虽然可以快速查找插入位置，但是无法优化所有元素右移这一操作的复杂度，实际复杂度变成了 $O(N\log N + N^2)$，不过还是快于普通的插入排序（因为查找这一过程得到了显著优化，比较的次数减少了）。

void insertionSort(vector<int>& a) {
    int n = a.size();
    for (int i = 1; i < n; i++) {
        int key = a[i];
        int p = upper_bound(a.begin(), a.begin() + i, key) - a.begin();
        for (int j = i; j > p; j--) {
            a[j] = a[j - 1];
        }
        a[p] = key;
    }
}

希尔排序

简单概括：

  1. 先将原序列划分为若干个子序列，划分方法是：先设置一个增量 $d$，然后原序列就可以划分为：
    • $A[0],A[d],A[2d],\ldots,A[kd]$；
    • $A[1],A[1+d],A[1+2d],\ldots,A[1+kd]$；
    • ……
    • $A[d-1],A[2d-1],A[3d-1],\ldots,A[-1+kd]$。
  2. 将上方这些子序列分别进行普通插入排序。
  3. 减小 $d$ 的值（比如每次除以 $3$），重复以上操作，直到 $d=1$。
希尔排序主要是利用了插入排序在“基本有序”的情况下复杂度近似线性的特征，因此有明显的加速效果。
// a是待排序数组，d是增量数组
void shellSort(vector<int>& a, vector<int>& d) {
    int n = a.size();
    for (auto& step : d) {
        for (int i = 0; i < step; i++) {
            for (int j = 1; i + step * j < n; j++) {
                int cur = i + step * j, key = a[cur];
                while (cur >= step && key < a[cur - step]) {
                    a[cur] = a[cur - step];
                    cur -= step;
                }
                a[cur] = key;
            }
        }
    }
}

希尔排序性质

  • 空间复杂度：显然和插入排序一致，$O(1)$。
  • 时间复杂度：取决于增量 $d$ 的取值序列，具体可以参考wiki。
  • 稳定性：不稳定。

冒泡排序

简单概括：从后往前或从前往后扫描序列，每次比较相邻的两个元素大小。以从前往后扫描为例，如果 $A[j]\gt A[j+1]$ 则交换这两个元素，那么经过 $i$ 轮冒泡排序之后，末尾的 $i$ 个元素一定是最大的 $i$ 个元素，且有序排列。

void bubbleSort(vector<int>& a) {
    int n = a.size();
    for (int i = n; i > 0; i--) {
        for (int j = 1; j < i; j++) {
            if (a[j] < a[j - 1]) {
                swap(a[j], a[j - 1]);
            }
        }
    }
}

也可以加上每趟排序后是否已经有序的特判：

void bubbleSort(vector<int>& a) {
    int n = a.size();
    for (int i = n; i > 0; i--) {
        bool ok = true;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[j - 1]) {
                swap(a[j], a[j - 1]);
                ok = false;
            }
        }
        if (ok) {
            return;
        }
    }
}

冒泡排序性质

  1. 空间复杂度：$O(1)$。
  2. 时间复杂度：如果采用了每趟排序后是否已经有序的特判，那么最优 $O(N)$，最劣 $O(N^2)$。平均时间复杂度 $O(N^2)$。
  3. 稳定性：稳定。

快速排序

核心思路：

  1. 假设我们当前需要对子序列 $A[l],A[l+1],\ldots,A[r]$ 进行排序。选择一个pivot（基准元素），将剩余的元素划分为两部分。左半部分都是 $\le$ pivot的元素，右半部分都是 $\ge$ pivot的元素。（partition操作）
  2. 完成一次划分之后，至少能够确保我们选定的pivot元素已经被摆放到了正确的位置，假设该位置是 $mid$ ，然后我们继续递归子序列 $A[l],A[l+1],\ldots,A[mid-1]$ 和 $A[mid+1],A[mid+2],\ldots,A[r]$ 。
  3. 重复上述过程，直到完成排序为止。

快速排序最关键的就是partition操作，但是该操作并没有严格规定，因此实际上实现策略很多。

下面给出一种策略：

  1. 每次选择 $[l,r]$ 中最左侧的元素作为 $pivot$，设置左指针 $lo$ 和右指针 $hi$，一开始分别指向 $A[l]$ 和 $A[r]$。
  2. $hi$ 指针检查 $A[hi]$ 是否小于 $pivot$，如果不满足，则 hi--；如果满足，则说明该元素应该丢到基准元素的左侧，此时可以直接将 $A[hi]$ 丢到 $lo$ 指针指向的位置。
  3. $lo$ 指针检查 $A[lo]$ 是否大于 $pivot$，如果不满足，则 lo++；如果满足，则说明该元素应该丢到基准元素的右侧，此时可以直接将 $A[lo]$ 丢到 $hi$ 指针指向的位置。
  4. 重复上述的 $2,3$ 两步，直到 $lo$ 和 $hi$ 指针指向了同一个位置，此时我们可以确定 $A[lo]$ 往左一定全部 $\le pivot$，$A[hi]$ 往右一定全部 $\ge pivot$，因此最后我们令 $A[lo]=pivot$ 即可完成一次partition。
void quickSort(vector<int>& a, int l, int r) {
    if (r <= l) return;

    int lo = l, hi = r, pivot = a[l];
    while (lo < hi) {
        while (lo < hi && a[hi] >= pivot) --hi;
        a[lo] = a[hi];
        while (lo < hi && a[lo] <= pivot) ++lo;
        a[hi] = a[lo];
    }
    a[lo] = pivot;

    quickSort(a, l, lo - 1);
    quickSort(a, lo + 1, r);
}
这个方法同样适用于选择任意一个元素作为pivot，假设我们选择了 $A[x](l\le x\le r)$ 作为pivot，那么我们可以先交换 $A[l]$ 和 $A[x]$，接下来继续按照以最左侧元素作为pivot的方法操作即可。

快速排序性质

  • 空间复杂度：一次 partition的空间复杂度是 $O(1)$（只需要一个pivot和左右指针即可）。因此总共的空间复杂度取决于递归时栈的深度，最优 $O(\log N)$，最劣 $O(N)$。平均 $O(\log N)$。
  • 时间复杂度：取决于递归次数，最优 $O(N\log N)$，最劣 $O(N^2)$。平均 $O(N\log N)$。
  • 稳定性：不稳定。（一个简单的例子是 $2,1,1$）

选择排序

一句话概括：第 $i$ 次遍历时，找到数组后 $i$ 个元素中最小的那个元素，然后将该元素放到第 $i-1$ 位。

void selectionSort(vector<int>& a) {
    int n = a.size();
    for (int i = 0; i < n; i++) {
        int minVal = a[i], pos = i;
        for (int j = i + 1; j < n; j++) {
            if (minVal > a[j]) {
                minVal = a[j];
                pos = j;
            }
        }
        swap(a[pos], a[i]);
    }
}

选择排序性质

  • 空间复杂度：O(1)。
  • 时间复杂度：最优、最劣、平均都是 O(N^2)。
  • 稳定性：不稳定。（一个简单的例子：2,2,1）

堆排序

一句话概括：用数组 $A[]$ 建立一个小根堆，然后每次弹出堆顶元素。

struct heap { // 小根堆
private:
    int n;
    vector<int> hp;

public:
    heap() : n(0) {}
    heap(const vector<int>& a) : n((int)a.size()), hp(a) { // O(N)建堆
        for (int i = (n - 1) / 2; i >= 0; i--) {
            modify(i);
        }
    }

    void modify(int p) { // 调整节点堆中的节点p
        for (;;) {
            int lc = 2 * p + 1, rc = lc + 1;
            int lv = (lc >= n ? INT_MAX : hp[lc]); // 左儿子的权值
            int rv = (rc >= n ? INT_MAX : hp[rc]); // 右儿子的权值
            if (hp[p] <= lv && hp[p] <= rv) {
                return;
            } else if (lv < rv) {
                swap(hp[p], hp[lc]);
                p = lc;
            } else {
                swap(hp[p], hp[rc]);
                p = rc;
            }
        }
    }

    int pop() { // 弹出堆顶元素
        int res = hp[0];
        swap(hp[--n], hp[0]);
        modify(0);
        return res;
    }
};

void heapSort(vector<int>& a) {
    int n = a.size();
    heap hp(a);
    for (int i = 0; i < n; i++) {
        a[i] = hp.pop();
    }
}
O(N)建堆

$O(N)$ 建堆的理论很简单，实际上就是利用了二叉堆是一个完全二叉树的性质。我们在建堆时，实际上只需要调整所有的非叶子节点，而在完全二叉树中，叶子节点的数量占总结点数的一半，因此我们在建堆时只需要调整前一半的节点就行了。

假设堆的高度为 $h$ ，若要调整第 $i$ 层的某个节点，那么至多将该节点下放 $h-i$ 次，并且完全二叉树第 $i$ 层的节点个数至多 $2^{i-1}$ 个，同时只有前一半的节点需要调整，因此可以计算出建堆的复杂度上限是 $4N$ ，即线性的复杂度。

堆排序性质

  • 空间复杂度：$O(1)$。（上方的实现并不是 $O(1)$ 的，构造了一个heap的结构体）
  • 时间复杂度：最优、最劣、平均均为 $O(N\log N)$。
  • 稳定性：不稳定。

归并排序

简单概括（二路归并）：

  1. 首先，如果我们需要将两个有序数组排序，显然有 $O(N)$ 的归并算法（双指针扫一圈）。
  2. 将待排序数组划分为 $\lceil \frac{n}{2}\rceil$ 个集合：
    • ${{A[0]},{A[1]}},{{A[2]},{A[3]}},{{A[4]},{A[5]}}\ldots$ 然后对上方的集合内部分别归并（相邻的集合两两合并），完成一轮归并后就有：
    • ${{A[0],A[1]},{A[2],A[3]}},{{A[4],A[5]},{A[6],A[7]}},\ldots$ 然后继续对上方的集合进行归并……直到最后只剩下一个集合。
  3. 显然，每次归并都会使得集合数量折半。
void mergeSort(vector<int>& a) {
    int n = a.size();
    vector<int> b(n);
    for (int d = 1; d < n; d <<= 1) {
        for (int i = 0, p = 0, q = d;; i++, p = q, q += d) {
            if (q >= n) break;
            // p是归并时的左指针 q是右指针
            int l = q, r = min(n, q + d); // l是左指针的右端点 r是右指针的右端点
            for (int j = p; j < r; j++) {
                if (p == l) {
                    b[j] = a[q++];
                } else if (q == r) {
                    b[j] = a[p++];
                } else if (a[p] < a[q]) {
                    b[j] = a[p++];
                } else {
                    b[j] = a[q++];
                }
            }
            for (int j = l - d; j < r; j++) {
                a[j] = b[j];
            }
        }
    }
}

归并排序性质

  • 空间复杂度：$O(N)$。（需要一个辅助数组暂存归并过程）
  • 时间复杂度：最优、最劣、平均都是 $O(N\log N)$。
  • 稳定性：稳定。

基数排序

简单概括（最低位优先LSD）：

  1. 基数排序（十进制下）是先准备 $10$ 个桶（链表），首先根据每个数的个位数字，将它们划分进这些桶中。完成一轮划分后，按照个位数字的大小，将每个桶中的数字依次取出（顺序是 $0,1,2,\cdots,9$），再存回数组 $A$。
  2. 然后，根据每个数的十位数字，将它们划分进这些桶中。完成一轮划分后，按照十位数字的大小，将每个桶中的数字依次取出（顺序是 $0,1,2,\cdots,9$），再存回数组 $A$。
  3. 然后，根据每个数的百位数字，将它们划分进这些桶中……
  4. 重复上述过程，直到枚举到了所有数字的最高位为止。
void radixSort(vector<int>& a) {
    const int N = 9; // 最高位位数
    int n = a.size();
    for (int i = 0, base = 1; i < N; i++, base *= 10) {
        vector<int> bucket[10];
        for (auto& j : a) {
            bucket[j / base % 10].emplace_back(j);
        }
        for (int j = 0, k = 0; j < 10; j++) {
            for (auto& e : bucket[j]) {
                a[k++] = e;
            }
        }
    }
}

最高位优先就是反过来，从最高位开始划分，本质上是完全一致的贪心。

基数排序性质

  • 空间复杂度：$O(N)$。（十个链表需要 $O(N)$ 的空间）
  • 时间复杂度：$O(ND)$，其中 $D$ 表示最大数字的位数。另一种说法是 $O(D(N+R))$，其中 $R$ 表示有几个桶（也就是加上合并链表的复杂度）。
  • 稳定性：稳定。

外部排序

外部排序（External sorting）是指能够处理极大量数据的排序算法。通常来说，外排序处理的数据不能一次装入内存，只能放在读写较慢的外存储器（通常是硬盘）上。

由于外部排序不能将数据全部读入内存，因此一般采用归并排序的思路来实现。

多路归并

假设现在要对大量的数据排序（假设一共 $2^{31}$ 个数字），那我们需要执行以下步骤：

  1. 首先将这些数据分为一系列的有序段（生成初始归并段）。这里简单起见，我们假设一共分成 $8$ 段，也就是说将这 $2^{31}$ 个数字分为 $8$ 个有序数组，每个数组 $2^{28}$ 个数字。
  2. 然后对这些有序数组执行二路归并排序，由于一个有 $8$ 段数字，因此需要执行总计 $3$ 趟归并排序。下面举例说明：
  3. 假设数据段分别为 $0,1,2,3,4,5,6,7$，那么第一趟归并之后，数据段 ${0,1},{2,3},{4,5},{6,7}$ 内部已经有序；
  4. 第二趟归并后 数据段 ${0,1,2,3},{4,5,6,7}$ 内部已经有序；
  5. 第三趟归并后，整个数组（$8$ 个数据段）就完成排序。

这里我们统计一下外部读写（I/O）的次数，这是因为内部排序算法的过程往往较快，而内存和硬盘之间的读写很慢，所以外部排序需要重点优化外部读写的次数。假设一个“磁盘块”进/出内存只需要一次读写，那么上面给出的例子中一趟二路归并就需要 $32$ 次I/O（$16$ 次读，$16$ 次写）。注意，这是因为多路归并的第一次划分每次会读入两个“磁盘块”，分别执行内部排序后写回磁盘。

于是，上方给出的多路归并的I/O次数就是：
$$
32+3\times 32=128
$$
第一个 $32$ 是生成初始归并段的I/O，后三个 $32$ 是 $3$ 趟归并的I/O。

减少I/O次数的一个有效方法是：执行多路归并。比如，我们改用 $4$ 路归并，那么我们就只需要 $2$ 趟归并就能完成排序了，于是I/O次数就减少为了：
$$
32+2\times 32=96
$$
一般地，对 $r$ 个初始归并段，作 $k$ 路归并排序，一共需要 $\lceil \log_k r\rceil$ 趟归并。因此减少I/O的主要方法就是两种：

  1. 增大 $k$。
  2. 减小 $r$ 。

败者树

多路归并虽然可以减少I/O次数，但是会增加内部归并时的比较次数（$k$ 路归并时，选出当前最小的元素需要 $k-1$ 次比较）。针对这一问题，我们可以用构造败者树的思想进行优化：

$5$ 路归并排序的败者树

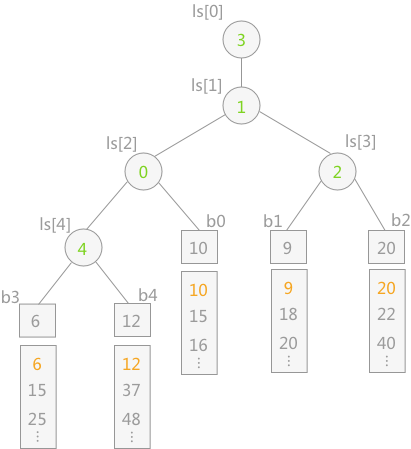
如图，这是一个 $5$ 路归并排序的败者树（败者树形式上近似于一个完全二叉树，和最小堆非常类似），每个非叶子节点记录了两个儿子节点中更大/小（取决于定义，图示是更大的节点，也就是比较的败者）的那个节点的下标（以 $ls[4]$ 为例，由于 $b3[0]=6\lt b4[0]=12$，因此权值为 $4$），然后胜者向上爬升一层，继续进行比较（以 $ls[2]$ 为例，由于 $ls[4]=4$，因此我们会比较 $b3[0]$ 和 $b0[0]$）。

构造一个 $k$ 路归并的败者树显然需要 $k-1$ 次比较。需要额外注意的是，败者树的最后一次比较会生成 $ls[0]$ 和 $ls[1]$ 两个节点（这是与完全二叉树唯一的不同点）。进行 $k$ 路归并时，败者树的树顶元素显然直接指向了当前最小元素的序列下标。

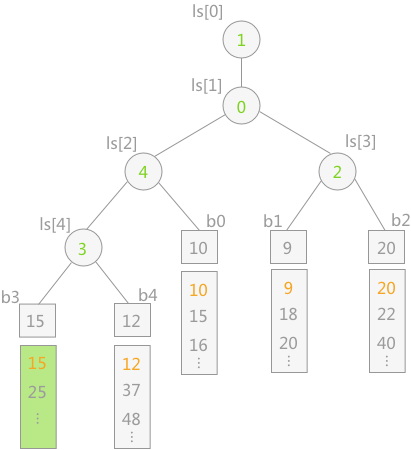
当我们取出了败者树的树顶元素（最小元素）后，如图所示，我们拿走了 $b3$ 序列的最小元素：

  • 此时 $b3$ 的最小元素转变为了 $15$，显然其父节点的权值也有可能发生变化。由于 $15\gt 12$，因此需要更新 $ls[4]=3$，然后继续向上更新。（图示就更新到这一步为止）
  • 由于 $b4$ 的队首元素 $12$ 大于 $b0$ 的队首元素 $10$，因此 $ls[2]$ 更新为 $4$，然后继续向上更新。
  • 由于 $b1$ 的队首元素 $9$ 小于 $b0$ 的队首元素 $10$，因此 $ls[1]$ 更新为 $0$，$ls[0]$ 更新为 $1$。

显然，$k$ 路归并的败者树进行一次更新的复杂度取决于树高，为 $O(\log k)$。

置换-选择排序

前面提到过，外部排序减少I/O有两种策略，策略1是多路归并，策略2是减少初始归并段数。置换-选择排序就是策略2的一种实现。

如上图，假设我们现在可用的内存空间为 $3$，那么按照一般策略，我们只能生成 $24\div 3=8$ 个初始段。但是，现在我们采用置换-选择排序生成初始段，过程如下：

  1. 维护一个大小为 $3$ 的小根堆，一开始将前 $3$ 个元素（$4,6,9$）丢进堆中，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $4$。
  2. 将 $7$ 丢进小根堆，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $6$。（已取出的序列是 $4,6$，堆中剩余两个元素分别是 $7,9$）
  3. 将 $13$ 丢进小根堆，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $7$。（已取出的序列是 $4,6,7$，堆中剩余两个元素分别是 $9,13$）
  4. 将 $11$ 丢进小根堆，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $9$。（已取出的序列是 $4,6,7,9$，堆中剩余两个元素分别是 $11,13$）
  5. 将 $16$ 丢进小根堆，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $11$。（已取出的序列是 $4,6,7,9,11$，堆中剩余两个元素分别是 $13,16$）
  6. 将 $14$ 丢进小根堆，然后取出堆顶元素，并记录此时已取出元素最小值的最大值为 $13$。（已取出的序列是 $4,6,7,9,11,13$，堆中剩余两个元素分别是 $14,16$）
  7. 将 $10$ 丢进小根堆，然后取出堆顶元素，堆顶元素是 $10$，但是已取出元素最小值的最大值为 $13$，因此 $10$ 是不能丢进当前的初始段中的。此时 $10$ 暂存，小根堆的大小减小 $1$，然后再取出堆顶元素并记录此时已取出元素最小值的最大值为 $14$。（已取出的序列是 $4,6,7,9,11,13,14$，堆中剩余一个元素是 $16$）
  8. ……
  9. 一直重复上述操作，直到小根堆的大小为 $0$。然后我们就需要开辟一段新的初始段了。（本例中，最终生成的第一个初始段为 $4,6,7,9,11,13,14,16,22,30$）

最佳归并树

当我们采用置换-选择排序算法生成初始归并段时，每个归并段的长度就不一定是相同的了。此时进行归并排序时，为了减少I/O次数，我们可以按照每个归并段的长度对他们重新排列，并构造出一棵最佳归并树。

一种三路归并树

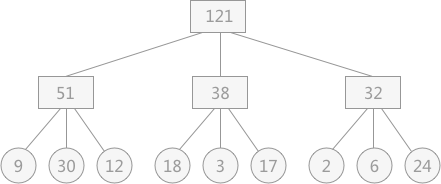
如上图，这是一个三路归并排序的归并树，叶子节点的权值表示数据段占用的“磁盘块”数量（也就是长度），那么这棵归并树的I/O次数实际上就是 $2\times WPL=2\times 2\times 121 = 484$ 次。（$WPL$ 就是树的带权路径长度，详见哈夫曼树）

容易发现，实际上最佳归并树就是广义哈夫曼树（$k$ 叉的哈夫曼树），因此构造策略也是和哈夫曼树完全一样的贪心策略。上图的最佳归并树如下图所示：

最佳归并树

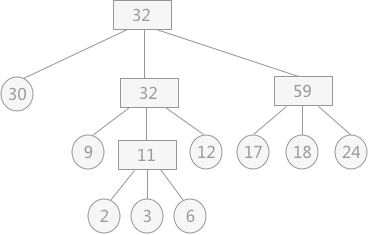
图中根节点的权值有误，实际上是 $121$（网上嫖的图，不改了）。

虚段

上方给出的例子是一个严格的三叉树，但是如果我们去掉一个节点（比如 $30$），那么构造出来的最佳归并树就至少有一个节点的度为 $2$。此时我们可以添加虚段（也就是点权为 $0$ 的点）使得最佳归并树可以成为严格的 $k$ 叉树，并在完成构造后删除这些权值为 $0$ 的虚段。

附带虚段的最佳归并树

那具体要添加多少个虚段呢？可以这么考虑：一个严格的 $k$ 叉树的叶子节点个数一定为 $1+(k-1)t$，其中 $t$ 是常数。也就是说，执行 $k$ 路归并时，如果有 $r$ 个初始段，需要补虚段直到 $r\bmod{(k-1)}\equiv 1$。

数据结构
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇