偏导数
定义
这里以对 $x$ 的偏导数为例,设有二元函数 $f(x,y)$ :
$$
f_x^\prime(x_0,y_0)=\lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x,x_0)-f(x_0,y_0)}{\Delta x} = \frac{\mathrm{d}}{\mathrm{d}x} f(x,y_0)\bigg|_{x=x_0}
$$
性质
如果函数 $z=f(x,y)$ 的两个二阶混合偏导数 $\frac{\partial^2 f}{\partial x\partial y},\frac{\partial^2 f}{\partial y\partial x}$ 在区域 $D$ 内连续,则在该区域内
$$
\frac{\partial^2 f}{\partial x\partial y}=\frac{\partial^2 f}{\partial y\partial x}
$$
全微分
若 $\Delta z=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)=A\Delta x+B\Delta y+O(\rho)$,则称函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微($\rho=\sqrt{\Delta x^2+\Delta y^2}$),并且全微分 $\mathrm{d}z = A\Delta x + B\Delta y$。
可微的必要条件
一元函数中,可微等价于可导。但是多元函数中只存在:可微必定可偏导,可偏导不一定可微。
可微的必要条件是:如果 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微,则在点 $(x_0,y_0)$ 处 $\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$ 必定存在,且
$$
\mathrm{d}z = \frac{\partial z}{\partial x} \mathrm{d}x + \frac{\partial z}{\partial y} \mathrm{d}y
$$
判断是否可微
判断可微一般有两个步骤:
- 判断偏导数 $f_x^\prime$ 和 $f_y^\prime$ 是否都存在。
- 判断 $\lim_{\Delta x,\Delta y\rightarrow 0}\frac{[f(x+\Delta x,y+\Delta y)-f(x,y)]-[f_x^\prime(x_0,y_0)\Delta x + f_y^\prime(x_0,y_0)\Delta y]}{\sqrt{\Delta x^2+\Delta y^2}}$ 是否为 $0$ 。
简单说一下上面那个复杂的式子是怎么得来的。
因为全微分的定义是 $\Delta z=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)=A\Delta x+B\Delta y+O(\rho)$,其中 $\rho=\sqrt{\Delta x^2+\Delta y^2}$,因此我们只需要证明 $\rho$ 是一个高阶无穷小。
并且由于此时偏导数 $f_x^\prime$ 和 $f_y^\prime$ 都存在,因此全微分如果存在就一定是 $\mathrm{d}z = \frac{\partial z}{\partial x} \mathrm{d}x + \frac{\partial z}{\partial y} \mathrm{d}y$ 的形式,因此必定有:
$$
\begin{aligned}
\Delta z&=A\Delta x+B\Delta y+O(\rho)\\
&=\frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y+O(\sqrt{\Delta x^2+\Delta y^2})\\
\Rightarrow\quad &\lim_{\Delta x,\Delta y\rightarrow 0} \frac{\Delta z – f_x(x_0,y_0)\Delta x – f_y(x_0,y_0)\Delta y}{\sqrt{\Delta x^2+\Delta y^2}}=0
\end{aligned}
$$
连续函数 $z=f(x,y)$ 满足 $\lim_{x\rightarrow 0,y\rightarrow 1}\frac{f(x,y)-2x+y-2}{\sqrt{x^2+(y-1)^2}}=0$ ,求 $\mathrm{d}z\big|_{(0,1)}$ 。
首先可以根据题设条件推出 $f(0,1)=1$ 。然后,给定的条件让人很容易联想到这就是判定是否可微的条件,因此我们变形一下:
$$
\begin{aligned}
\lim_{x\rightarrow 0,y\rightarrow 1}\frac{f(x,y)-2x+y-1}{\sqrt{x^2+(y-1)^2}}=0\Leftrightarrow \lim_{x\rightarrow 0,y\rightarrow 1}\frac{[f(x,y)-f(0,1)]-[2x-(y-1)]}{\sqrt{x^2+(y-1)^2}}=0
\end{aligned}
$$
因此 $\mathrm{d}z\big|_{(0,1)} = 2\mathrm{d}x-\mathrm{d}y$ 。
可微的充分条件
如果 $z=f(x,y)$ 的偏导数 $\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$ 在点 $(x_0,y_0)$ 处连续,则函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微。
多元函数连续、可导、可微之间的关系
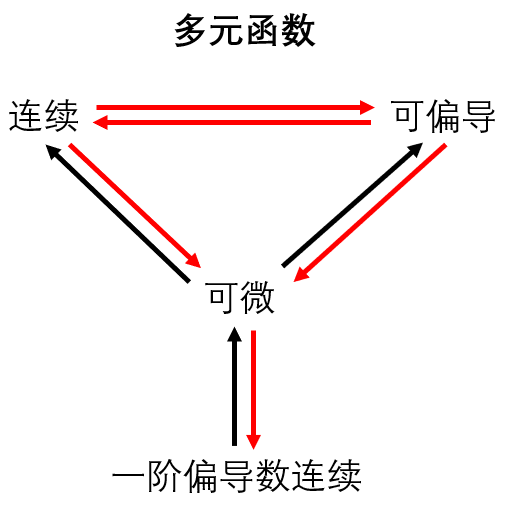
经典反例
首先,证明连续其实就是证明极限存在,因此有:
$$
\begin{aligned}
\lim_{x\rightarrow 0,y\rightarrow 0}f(x,y) = 0
\end{aligned}
$$
因此,显然连续。然后证不可偏导,由于是对称式,因此以 $f_x^\prime$ 为例:
$$
\begin{aligned}
f_x^\prime (0,0) &= \frac{\mathrm{d}}{\mathrm{d} x} f(x,0)\\
&= |x|
\end{aligned}
$$
该函数在 $x\rightarrow 0$ 时显然不连续。
先证可导,由于是对称式,以 $f_x^\prime$ 为例:
$$
\begin{aligned}
f_x^\prime (0,0) &= \frac{\mathrm{d}}{\mathrm{d} x} f(x,0)\
&= \begin{cases}\frac{x\cdot 0}{x^2+0^2}=0 & (x,y)\neq (0,0)\\ 0 & (x,y)=(0,0)\end{cases}\
&= 0
\end{aligned}
$$
再证不连续,假设我们按照 $y=kx$ 这条直线逼近 $(0,0)$ 那么 $\lim_{x\rightarrow 0,y\rightarrow 0}$ 就可以表示为:
$$
\begin{aligned}
\lim_{x\rightarrow 0,y\rightarrow 0} &= \lim_{x\rightarrow 0} f(x,kx)\
&= \begin{cases}\frac{kx^2}{x^2+k^2x^2}=\frac{k}{1+k^2} & (x,y)\neq (0,0)\\ 0 & (x,y)=(0,0)\end{cases}
\end{aligned}
$$
因此极限不存在,推出该函数在 $(0,0)$ 不连续。
先证可导,由于是对称式,以 $f_x^\prime$ 为例:
$$
\begin{aligned}
f_x^\prime (0,0) &= \frac{\mathrm{d}}{\mathrm{d} x} f(x,0)\\
&= \begin{cases}\frac{x\cdot 0}{\sqrt{x^2+0^2}}=0 & (x,y)\neq (0,0)\\ 0 & (x,y)=(0,0)\end{cases}\\
&= 0
\end{aligned}
$$
然后证明不可微,由于该函数可偏导,因此我们需要利用那个比较复杂的定义推广来证明:
$$
\begin{aligned}
&\lim_{\Delta x,\Delta y\rightarrow 0}\frac{[f(x+\Delta x,y+\Delta y)-f(x,y)]-[f_x^\prime(x_0,y_0)\Delta x + f_y^\prime(x_0,y_0)\Delta y]}{\sqrt{\Delta x^2+\Delta y^2}} \\
=& \lim_{\Delta x,\Delta y\rightarrow 0}\frac{[f(0+\Delta x,0+\Delta y)-f(0,0)] – [f_x^\prime(0,0)\Delta x + f_y^\prime(0,0)\Delta y]}{\sqrt{\Delta x^2+\Delta y^2}}\\
=& \lim_{\Delta x,\Delta y\rightarrow 0}\frac{[\frac{\Delta x\Delta y}{\sqrt{\Delta x^2+\Delta y^2}}-0] – [0 + 0]}{\sqrt{\Delta x^2+\Delta y^2}}\\
=& \lim_{\Delta x,\Delta y\rightarrow 0}\frac{\Delta x\Delta y}{\Delta x^2+\Delta y^2}
\end{aligned}
$$
这个极限显然不存在(前面出现过了)。因此不满足可微的判定条件。
可微的判定一般是两个判定,首先判 $(0,0)$ 的偏导是否存在。
$$
\begin{aligned}
f_x(0,0)&=\frac{\mathrm{d}}{\mathrm{d} x} f(x,0)\\
&=\begin{cases}x^2\sin\frac{1}{x^2}\rightarrow 0&(x,y)\neq(0,0)\\0&(x,y)=(0,0)\end{cases}
\end{aligned}
$$
因此偏导存在,然后进行第二个判定:
$$
\begin{aligned}
&\lim_{\Delta x,\Delta y\rightarrow 0}\frac{[f(x+\Delta x,y+\Delta y)-f(x,y)]-[f_x^\prime(x_0,y_0)\Delta x + f_y^\prime(x_0,y_0)\Delta y]}{\sqrt{\Delta x^2+\Delta y^2}} \\
=& \lim_{\Delta x,\Delta y\rightarrow 0}\frac{[(\Delta x^2+\Delta y^2)\sin\frac{1}{\Delta x^2 + \Delta y^2}-0]-[0+0]}{\sqrt{\Delta x^2+\Delta y^2}}\\
=& \lim_{\Delta x,\Delta y\rightarrow 0}(\sqrt{\frac{\Delta x^4}{\Delta x^2+\Delta y^2}}+\sqrt{\frac{\Delta y^4}{\Delta x^2 + \Delta y^2}})\sin\frac{1}{\Delta x^2 + \Delta y^2}\\
=& \ 0
\end{aligned}
$$
综上所述,该函数可微。接下来证明偏导不连续,这只需要求出 $f_x^\prime$ :
$$
\begin{aligned}
f_x^\prime &= 2x\sin\frac{1}{x^2+y^2} – \frac{2x}{x^2+y^2}\cos\frac{1}{x^2+y^2}\\
\end{aligned}
$$
以 $y=0,x\rightarrow 0$ 为例求极限:
$$
\begin{aligned}
\lim_{y=0,x\rightarrow 0} f^\prime_x &= 2x\sin\frac{1}{x^2} – \frac{2x}{x^2}\cos\frac{1}{x^2}\\
&= 0-\frac{2}{x}\cos \frac{1}{x^2}
\end{aligned}
$$
显然极限不存在,因此 $(0,0)$ 点的偏导数不连续。
多元函数求导
多元复合函数求导
核心思路就是链式法则!!!
设 $z=(1+x^2+y^2)^{xy}$ ,求 $\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$ 。
方法一,转化为幂指函数然后暴力求导,以 $\frac{\partial z}{\partial x}$ 为例:
$$
\begin{aligned}
\frac{\partial z}{\partial x} &= \frac{\partial}{\partial x}(e^{xy\ln(1+x^2+y^2)})\\
&=\frac{\partial(xy\ln(1+x^2+y^2))}{\partial x}\times e^{xy\ln(1+x^2+y^2)}\\
&= \bigg[y\ln(1+x^2+y^2)+ xy\frac{\partial \ln(1+x^2+y^2)}{\partial x}\bigg]\times (1+x^2+y^2)^{xy}\\
&= \bigg[y\ln(1+x^2+y^2) + \frac{2x^2y}{1+x^2+y^2}\bigg]\times (1+x^2+y^2)^{xy}\\
&= (1+x^2+y^2)^{xy}\bigg[ \frac{2x^2y}{1+x^2+y^2}+y\ln(1+x^2+y^2) \bigg]
\end{aligned}
$$
方法二,复合多元函数求导,以 $\frac{\partial z}{\partial y}$ 为例,令 $u = 1+x^2+y^2,v=xy$ ,则原函数转化为 $z=f(u,v)=u^v$ 。
$$
\begin{aligned}
\frac{\partial z}{\partial y} &= \frac{\partial z}{\partial u}\frac{\partial u}{\partial y} + \frac{\partial z}{\partial v}\frac{\partial v}{\partial y}\\
&= \frac{\partial e^{v\ln u}}{\partial u}\cdot 2y + \frac{\partial e^{v\ln u}}{\partial v}\cdot x\\
&= \frac{v}{u}\cdot e^{v\ln u}\cdot 2y + \ln u\cdot e^{v\ln u}\cdot x\\
&= (1+x^2+y^2)^{xy}\bigg[ \frac{2xy^2}{1+x^2+y^2} + x\ln(1+x^2+y^2) \bigg]
\end{aligned}
$$
设 $w=f(x+y+z,xyz)$ ,$f$ 具有二阶连续偏导数,求 $\frac{\partial w}{\partial x}$ 和 $\frac{\partial^2w}{\partial x\partial z}$ 。
令 $u=x+y+z,v=xyz$ 则有:
$$
\begin{aligned}
\frac{\partial w}{\partial x} &= \frac{\partial w}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial w}{\partial v}\frac{\partial v}{\partial x}\\
&= f_u^\prime \cdot 1 + f_v^\prime\cdot yz\\
&= f_u^\prime + yzf_v^\prime
\end{aligned}
$$
$$
\begin{aligned}
\frac{\partial^2w}{\partial x\partial z} &= \frac{\partial}{\partial z}(\frac{\partial w}{\partial x})\\
&= \frac{\partial}{\partial z}(f_u^\prime + yzf_v^\prime)\\
&= [\frac{\partial f_u^\prime}{\partial u}\frac{\partial u}{\partial z}+\frac{\partial f_u^\prime}{\partial v}\frac{\partial v}{\partial z}] + [yf_v^\prime + yz\frac{\partial f_v^\prime}{\partial u}\frac{\partial u}{\partial z}+yz\frac{\partial f_v^\prime}{\partial v}\frac{\partial v}{\partial z}]\\
&= f_{uu}^\prime + xyf_{uv}^\prime + yf_v^\prime + yzf_{vu}^\prime + xy^2zf_{vv}^\prime\\
&= f_{uu}^\prime + (xy+yz)f_{uv}^\prime + yf_v^\prime + xy^2zf_{vv}^\prime
\end{aligned}
$$
设 $z=xyf(\frac{y}{x})$,$f(u)$ 可导,求 $xz_x^\prime + yz_y^\prime$。
容易错的点在于:$f(\frac{y}{x})$ 的求导,以 $f_x(\frac{y}{x})^\prime$ 为例,令 $u=\frac{y}{x}$ 则有
$$
f_x(\frac{y}{x})^\prime = \frac{\partial f}{\partial u}\frac{\partial u}{\partial x} = f^\prime\times -yx^{-2}
$$
因此本题的答案为 $2z$。
隐函数求导
一个方程的情形
设 $F(x,y)$ 有连续一阶偏导数,且 $F_y^\prime\neq 0$ ,则由方程 $F(x,y)=0$ 确定的函数 $y=y(x)$ 可导,且
$$
\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{F_x^\prime}{F_y^\prime}
$$
如果 $y$ 如果可以显化,那我们就可以表示为 $y=f(x)$,因此这里有一个不严谨的推导:
$$
\begin{aligned}
F(x,y)=0&\Rightarrow \frac{\mathrm{d}}{\mathrm{d}x}F(x,y)=0\\
&\Rightarrow F_x^\prime + \frac{\partial F}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}x}=0\\
&\Rightarrow \frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{F_x^\prime}{F_y^\prime}
\end{aligned}
$$
设 $\ln\sqrt{x^2+y^2}=\arctan\frac{y}{x}$ ,求 $\frac{\mathrm{d}y}{\mathrm{d}x}$ 。
设 $F(x,y) = \ln\sqrt{x^2+y^2}-\arctan\frac{y}{x}$ ,于是就有 $\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{F_x^\prime}{F_y^\prime}$ :
$$
\begin{aligned}
F_x^\prime =\frac{x+y}{x^2+y^2}, \quad F_y^\prime = \frac{y-x}{x^2+y^2}
\end{aligned}
$$
因此:
$$
\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{F_x^\prime}{F_y^\prime}=\frac{x+y}{x-y}
$$
*一元函数里的隐函数做法($y=f(x)$)也是可行的,就是计算量更大一些。或者说,这其实就是一元函数隐函数求导。
设 $F(x,y,z)$ 有连续一阶偏导数,且 $F_z^\prime\neq 0,z=z(x,y)$ 由方程 $F(x,y,z)=0$ 所确定,则
$$
\begin{aligned}
\frac{\partial z}{\partial x} = -\frac{F_x^\prime}{F_z^\prime},\quad \frac{\partial z}{\partial y} = -\frac{F_y^\prime}{F_z^\prime}
\end{aligned}
$$
类似于一元函数,也可以用同样的不严谨方法推导,略。
设 $x^2+y^2+z^2-4z=0$ ,求 $\frac{\partial^2z}{\partial x^2}$ 。
显然是一个隐函数,可以写成以下形式:$F(x,y,z) = F(x,y,f(x,y))$ ,其中 $z=f(x,y)$ 。
$$
\begin{aligned}
x^2+y^2+z^2-4z=0&\Rightarrow \frac{\partial}{\partial x} (x^2+y^2+z^2-4z)=0\\
&\Rightarrow 2x + \frac{\partial z}{\partial x}\cdot2z-4\frac{\partial z}{\partial x} = 0\\
&\Rightarrow \frac{\partial z}{\partial x} = \frac{x}{2-z}\\
&\Rightarrow \frac{\partial}{\partial x}\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}\frac{x}{2-z}\\
&\Rightarrow \frac{\partial^2z}{\partial x^2}=\frac{\frac{\partial}{\partial x}x\cdot(2-z) – x\cdot\frac{\partial}{\partial x}(2-z)}{(2-z)^2}\\
&\Rightarrow \frac{\partial^2z}{\partial x^2}=\frac{(2-z)+x\frac{\partial z}{\partial x}}{(2-z)^2}\\
&\Rightarrow \frac{\partial^2z}{\partial x^2}=\frac{(2-z)^2+x^2}{(2-z)^3}
\end{aligned}
$$
设 $\frac{x}{z}=\ln \frac{z}{y}$ ,求 $\frac{\partial z}{\partial x}$ 以及 $\frac{\partial z}{\partial y}$ 。
令 $F(x,y,z) = \frac{x}{z}-\ln \frac{z}{y}$ ,则有:
$$
\begin{aligned}
F_x^\prime&=\frac{1}{z}\\
F_y^\prime&=-(-\frac{z}{y^2}\cdot\frac{y}{z})=\frac{1}{y}\\
F_z^\prime&=-\frac{x}{z^2}-\frac{1}{y}\cdot\frac{y}{z}=-\frac{x+z}{z^2}
\end{aligned}
$$
因此:
$$
\frac{\partial z}{\partial x} = \frac{z}{x+z},\quad\frac{\partial z}{\partial y}=\frac{z^2}{y(x+z)}
$$
设 $\Phi(u,v)$ 具有连续偏导数,证明由方程 $\Phi(cx-az,cy-bz)=0$ 所确定的函数 $z=f(x,y)$ 满足 $a\frac{\partial z}{\partial x}+b\frac{\partial z}{\partial y}=c$ 。
令 $u=cx-az,v=cy-bz$ ,则有:
$$
\begin{aligned}
\Phi_x^\prime&= \frac{\partial \Phi}{\partial u}\frac{\partial u}{\partial x}=c\Phi_u^\prime\\
\Phi_y^\prime&= \frac{\partial \Phi}{\partial v}\frac{\partial v}{\partial y}=c\Phi_v^\prime\\
\Phi_z^\prime&= \frac{\partial \Phi}{\partial u}\frac{\partial u}{\partial z}+\frac{\partial \Phi}{\partial v}\frac{\partial v}{\partial z}=-a\Phi_u^\prime-b\Phi_v^\prime
\end{aligned}
$$
此外,根据 $\frac{\partial z}{\partial x} = -\frac{F_x^\prime}{F_z^\prime},\frac{\partial z}{\partial y} = -\frac{F_y^\prime}{F_z^\prime}$ ,我们就可以得出:
$$
a\frac{\partial z}{\partial x}+b\frac{\partial z}{\partial y}=-a\frac{\Phi_x^\prime}{\Phi_z^\prime}-b\frac{\Phi_y^\prime}{\Phi_z^\prime}=c
$$
方程组的情形
设 $u=u(x),v=v(x)$ 由方程组 $\begin{cases}F(x,u,v)=0\\ G(x,u,v)=0\end{cases}$ 所确定,要求 $\frac{\mathrm{d}u}{\mathrm{d}x}$ 和 $\frac{\mathrm{d}v}{\mathrm{d}x}$ 。可通过原方程组两端对 $x$ 求导得到,即:
$$
\begin{cases}
F_x^\prime+F_u^\prime\frac{\mathrm{d}u}{\mathrm{d}x}+F_v^\prime\frac{\mathrm{d}v}{\mathrm{d}x}=0\\
G_x^\prime+G_u^\prime\frac{\mathrm{d}u}{\mathrm{d}x}+G_v^\prime\frac{\mathrm{d}v}{\mathrm{d}x}=0
\end{cases}
$$
然后,二元一次方程组消元:
$$
\begin{aligned}
&G_v^\prime\bigg[F_x^\prime+F_u^\prime\frac{\mathrm{d}u}{\mathrm{d}x}+F_v^\prime\frac{\mathrm{d}v} {\mathrm{d}x}\bigg] = F_v^\prime\bigg[G_x^\prime+G_u^\prime\frac{\mathrm{d}u}{\mathrm{d}x}+G_v^\prime\frac{\mathrm{d}v}{\mathrm{d}x}\bigg]=0\\
\Rightarrow &\ G_v^\prime F_x^\prime + G_v^\prime F_u^\prime\frac{\mathrm{d}u} {\mathrm{d}x} = F_v^\prime G_x^\prime + F_v^\prime G_u^\prime \frac{\mathrm{d}u} {\mathrm{d}x}\\
\Rightarrow &\ G_v^\prime F_x^\prime – F_v^\prime G_x^\prime = \frac{\mathrm{d}u} {\mathrm{d}x}(F_v^\prime G_u^\prime-G_v^\prime F_u^\prime)\\
\Rightarrow &\ \frac{\mathrm{d}u} {\mathrm{d}x} = \frac{F_v^\prime G_x^\prime-G_v^\prime F_x^\prime}{G_v^\prime F_u^\prime-F_v^\prime G_u^\prime}\\
\Rightarrow &\ \frac{\mathrm{d}u} {\mathrm{d}x} = \frac{F_x^\prime G_u^\prime-F_u^\prime G_x^\prime}{G_v^\prime F_u^\prime-F_v^\prime G_u^\prime}
\end{aligned}
$$
当然,这里实际上可以直接通过克莱默法则推导。
对于一个二元一次方程组 $\begin{cases}a_1 x + b_1 y = c_1\\ a_2x + b_2y=c_2\end{cases}$ ,记行列式 $D = \det\begin{bmatrix} a_1 & b_1\\ a_2 & b_2 \end{bmatrix} ,D_x = \det\begin{bmatrix} c_1 & b_1\\ c_2 & b_2 \end{bmatrix}, D_y = \det\begin{bmatrix} a_1 & c_1\\ a_2 & c_2 \end{bmatrix}$ ,且 $D\neq 0$ 则方程组的解集为 $x=\frac{D_x}{D},y=\frac{D_y}{D}$ 。
设 $\begin{cases}z=x^2+y^2\\x^2+2y^2+3z^2=20\end{cases}$ ,求 $\frac{\mathrm{d}y}{\mathrm{d}x},\frac{\mathrm{d}z}{\mathrm{d}x}$ 。
该方程组对 $x$ 求导,整理后得到:
$$
\begin{cases}
\frac{\mathrm{d}z}{\mathrm{d}x}-2y\frac{\mathrm{d}z}{\mathrm{d}y}=2x\\
6z\frac{\mathrm{d}z}{\mathrm{d}x}+4y\frac{\mathrm{d}y}{\mathrm{d}x}=-2x
\end{cases}
$$
用克莱默法则求出:
$$
\begin{cases}
\frac{\mathrm{d}z}{\mathrm{d}x} = \frac{\det
\begin{bmatrix}
2x & -2y\\
-2x & 4y
\end{bmatrix}}{\det
\begin{bmatrix}
1 & -2y\\
6z & 4y
\end{bmatrix}}
= \frac{x}{3z+1}\\
\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\det
\begin{bmatrix}
1 & 2x\\
6z & -2x
\end{bmatrix}
}{\det
\begin{bmatrix}
1 & -2y\\
6z & 4y
\end{bmatrix}}
= -\frac{x(1+6z)}{2y(1+3z)}
\end{cases}
$$
设 $y=f(x,t)$ ,而 $t=t(x,y)$ 是由方程 $F(x,y,t)=0$ 所确定的函数,其中 $f,F$ 都具有一阶连续偏导数。证明:
$$
\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\frac{\partial f}{\partial x}\frac{\partial F}{\partial t}-\frac{\partial f}{\partial t}\frac{\partial F}{\partial x}}{\frac{\partial f}{\partial t}\frac{\partial F}{\partial y}+\frac{\partial F}{\partial t}}
$$
题设条件给的信息翻译一下,实际上就是:
- 给定方程组 $y=f(x,t),F(x,y,t)=0$ 。
- $y$ 可以由 $x,t$ 决定,$t$ 可以由 $x,y$ 决定;这其实就是说 $y=y(x),t=t(x)$,即 $y,t$ 都可以表示为有关 $x$ 的一元隐函数。
因此,方程组对 $x$ 求导得到:
$$
\begin{cases}
\frac{\mathrm{d}y}{\mathrm{d}x}-\frac{\partial f}{\partial t}\frac{\mathrm{d}t}{\mathrm{d}x}=\frac{\partial f}{\partial x}\\
\frac{\partial F}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}x}+\frac{\partial F}{\partial t}\frac{\mathrm{d}t}{\mathrm{d}x}=-\frac{\partial F}{\partial x}
\end{cases}
$$
用克莱默法则直接求出 $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\frac{\partial f}{\partial x}\frac{\partial F}{\partial t}-\frac{\partial f}{\partial t}\frac{\partial F}{\partial x}}{\frac{\partial f}{\partial t}\frac{\partial F}{\partial y}+\frac{\partial F}{\partial t}}$ 。
设 $u=u(x,y),v=v(x,y)$ 由方程组 $\begin{cases}F(x,y,u,v)=0\\G(x,y,u,v)=0\end{cases}$ 所确定,要求 $\frac{\partial u}{\partial x}$ 和 $\frac{\partial v}{\partial x}$ 。可通过对原方程组两端对 $x$ 求导得到,即:
$$\begin{cases}
F_x^\prime+F_u^\prime\frac{\partial u}{\partial x}+F_v^\prime\frac{\partial v}{\partial x}=0\\
G_x^\prime+G_u^\prime\frac{\partial u}{\mathrm{d}x}+G_v^\prime\frac{\partial v}{\partial x}=0
\end{cases}$$
然后就可以使用克莱默法则推出结论:
\begin{cases}
\frac{\partial u}{\partial x} &= \frac{\det\begin{bmatrix} -F_x^\prime & F_v^\prime\\ -G_x^\prime & G_v^\prime \end{bmatrix}}{ \det\begin{bmatrix} F_u^\prime & F_v^\prime\\ G_u^\prime & G_v^\prime \end{bmatrix} }\\
\frac{\partial v}{\partial x} &= \frac{\det\begin{bmatrix} F_u^\prime & -F_x^\prime\\ G_u^\prime & -G_x^\prime \end{bmatrix}}{ \det\begin{bmatrix} F_u^\prime & F_v^\prime\\ G_u^\prime & G_v^\prime \end{bmatrix} }
\end{cases}
设 $\begin{cases}x=e^u+u\sin v\\ y=e^u-u\cos v\end{cases}$ ,求 $\frac{\partial u}{\partial x},\frac{\partial v}{\partial x},\frac{\partial u}{\partial y},\frac{\partial v}{\partial y}$ 。
这里,显然 $u,v$ 是 $x,y$ 的隐函数,该方程组两边同时对 $x$ 求导,整理后得到:
$$
\begin{cases}
(e^u+\sin v)\frac{\partial u}{\partial x} + u\cos v\frac{\partial v}{\partial x} = 1\\
(e^u-\cos v)\frac{\partial u}{\partial x} +u\sin v \frac{\partial v}{\partial x} = 0\\
\end{cases}
$$
由克莱默法则:
$$
\begin{cases}
D = \det
\begin{bmatrix}
e^u+\sin v & u\cos v\\
e^u – \cos v & u\sin v
\end{bmatrix}
=u\bigg[e^u(\sin v – \cos v) + 1\bigg]\\
D_x=\det
\begin{bmatrix}
1 & u\cos v\\
0 & u\sin v
\end{bmatrix}
=u\sin v\\
D_y=\det
\begin{bmatrix}
e^u+\sin v & 1\\
e^u – \cos v & 0
\end{bmatrix}
=\cos v – e^u\\
\end{cases}
$$
解出:
$$
\frac{\partial u}{\partial x} = \frac{D_x}{D}=\frac{\sin v}{e^u(\sin v -\cos v)+1},\quad\frac{\partial v}{\partial x}=\frac{D_y}{D}=\frac{\cos v-e^u}{u\big[e^u(\sin v – \cos v) + 1\big]}
$$
同理:
$$
\frac{\partial u}{\partial y}=\frac{-\cos v}{e^u(\sin v -\cos v)+1},\quad\frac{\partial v}{\partial y}=\frac{\sin v+e^u}{u\big[e^u(\sin v – \cos v) + 1\big]}
$$
几何应用
空间曲线的切线和法平面
点向式/参数式
设空间曲线 $L$ 的参数方程为 $\begin{cases}x=\varphi(y)\\ y=\psi(t)\\ z=\omega(t)\end{cases}$ ,则该曲线上一点 $P(x_0,y_0,z_0)$(该点参数设为 $t_0$,且 $x^\prime(t_0),y^\prime(t_0),z^\prime(t_0)$ 不同时为零)处的切向量为 $\vec{\tau}=(x^\prime(t_0),y^\prime(t_0),z^\prime(t_0))$ 。由此推出
- 点 $P$ 处的切线方程为 $\frac{x-x_0}{x^\prime(t_0)} = \frac{y-y_0}{y^\prime(t_0)}=\frac{z-z_0}{z^\prime(t_0)}$ 。
- 点 $P$ 处的法平面方程为 $x^\prime(t_0)(x-x_0)+y^\prime(t_0)(y-y_0)+z^\prime(t_0)(z-t_0)=0$ 。
求曲线 $x=\frac{t}{1+t},y=\frac{1+t}{t},z=t^2$ 在对应于 $t_0=1$ 的点处的切线及法平面方程。
对 $t$ 求导:
$$
f_x^\prime=\frac{1}{(1+t)^2},f_y^\prime=-\frac{1}{t^2},f_z^\prime=2t
$$
因此切线方程为 $\frac{x-0.5}{1}=\frac{y-2}{-4}=\frac{z-1}{8}$ ;法平面方程为 $1(x-0.5)-(y-2)+2(z-1)=0$,即 $2x-8y+16z-1=0$ 。
一般式
设空间曲线 $L$ 的方程为一般式 $\begin{cases}F(x,y,z)=0\\ G(x,y,z)=0\end{cases}$ ,则该曲线上一点 $P(x_0,y_0,z_0)$ 处的切向量的计算方法如下。
$$
\begin{aligned}
\text{Let }&\vec{n_1}=(F_x^\prime(x_0,y_0,z_0),F_y^\prime(x_0,y_0,z_0),F_z^\prime(x_0,y_0,z_0)), \\ &\vec{n_2}=(G_x^\prime(x_0,y_0,z_0),G_y^\prime(x_0,y_0,z_0),G_z^\prime(x_0,y_0,z_0)).
\end{aligned}
$$
切向量可以表示为 $\vec{n_1}\times\vec{n_2}$ ,即:
$$
\begin{aligned}
\vec{n_1}\times\vec{n_2} &= \det
\begin{bmatrix}
i&j&k\\
F_x^\prime&F_y^\prime&F_z^\prime\\
G_x^\prime&G_y^\prime&G_z^\prime
\end{bmatrix}\\
&=(\det
\begin{bmatrix}
F_y^\prime&F_z^\prime\\
G_y^\prime&G_z^\prime\\
\end{bmatrix},
\det\begin{bmatrix}
F_z^\prime&F_x^\prime\\
G_z^\prime&G_x^\prime\\
\end{bmatrix},
\det\begin{bmatrix}
F_x^\prime&F_y^\prime\\
G_x^\prime&G_y^\prime\\
\end{bmatrix}
)
\end{aligned}
$$
求曲线 $x^2+y^2+z^2=6,x+y+z=0$ 在点 $(1,-2,1)$ 处的切线及法平面方程。
先求偏导:
$$
F_x^\prime=2x,F_y^\prime=2y,F_z^\prime=2x;G_x^\prime=1,G_y^\prime=1,G_z^\prime=1
$$
直接按照结论推出该点的方向向量为 $\vec{\tau}=(2y-2z,2z-2x,2x-2y)=(-6,0,6)\Rightarrow(1,0,-1)$ ,因此可以解出切线方程为:$\frac{x-1}{1}=\frac{y+2}{0}=\frac{z-1}{-1}$ ;法平面方程为 $1(x-1)+0(y+2)+(-1)(z-1)=0$ 。
空间曲面的切平面和法线
设曲面 $\Sigma$ 的方程为 $F(x,y,z)=0$ ,并设曲面上一点 $P(x_0,y_0,z_0)$ 的三个偏导数 $(F_x^\prime(x_0,y_0,z_0),F_y^\prime(x_0,y_0,z_0),F_z^\prime(x_0,y_0,z_0))$ 不同时为零,则该曲面在点 $P$ 处的法向量是:
$$
\vec{n}=(F_x^\prime(x_0,y_0,z_0),F_y^\prime(x_0,y_0,z_0),F_z^\prime(x_0,y_0,z_0))
$$
由此推出($F_x^\prime(x_0,y_0,z_0)$ 简写为 $F_x^\prime$,以此类推):
- 切平面方程为 $F_x^\prime(x-x_0)+F_y^\prime(y-y_0)+F_z^\prime(z-z_0)=0$。
- 法线方程为 $\frac{x-x_0}{F_x^\prime}=\frac{y-y_0}{F_y^\prime}=\frac{z-z_0}{F_z^\prime}$ 。
求球面 $x^2+y^2+z^2=14$ 在点 $(1,2,3)$ 处的切平面及法线方程。
先求点 $(1,2,3)$ 处的偏导数就可以得到法向量为 $(2,4,6)$ ,化简后即 $\vec{n}=(1,2,3)$ 。
因此切平面是 $1(x-1)+2(y-2)+3(z-3)=0$ ,整理一下:$x+2y+3z-14=0$;法线方程为 $\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}$ ,整理一下:$\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ 。
在曲面 $z=xy$ 上求一点,使这点处的发现垂直于平面 $x+3y+z+9=0$ ,并求出该点法线方程。
假设该点为 $P(x_0,y_0,z_0)$ ,由于该点法线垂直于平面 $x+3y+z+9=0$ ,因此该点法向量即 $(1,3,1)$ ,同时根据曲面上一点的法向量公式得到点 $P$ 的法向量为(令 $f:xy-z=0$):
$$
\vec{n_P}=(f_x^\prime,f_y^\prime,f_z^\prime)=(y_0,x_0,-1)
$$
于是解出点 $P$ 坐标为 $(-3,-1,-1)$ ,该点的法线方程为 $\frac{x+3}{1}=\frac{y+1}{3}=\frac{z-3}{1}$ 。
方向导数与梯度
方向导数
如果函数 $z=f(x,y)$ 在点 $P(x_0,y_0)$ 处可微,那么函数在该点沿任意方向 $l$ 的方向导数存在,且
$$
\begin{aligned}
\frac{\partial f}{\partial l}\bigg|_{(x_0,y_0)}&=f_x^\prime(x_0,y_0)\cos\alpha+f_y^\prime(x_0,y_0)\cos\beta\\
&=(f_x^\prime(x_0,y_0),f_y^\prime(x_0,y_0))\cdot\vec{e}
\end{aligned}
$$
这里,$\vec{e}$ 就是 $(\cos\alpha,\cos\beta)$ ,即方向 $l$ 的单位方向向量。
这个结论也可以推广到三维情形,略。
求函数 $z=xe^{2y}$ 在点 $P(1,0)$ 处沿从点 $P(1,0)$ 到点 $Q(2,-1)$ 的方向的方向导数。
$$
\begin{aligned}
\frac{\partial f}{\partial l}\bigg|_{(1,0)}&=f_x^\prime(1,0)\cos\alpha+f_y^\prime(1,0)\cos\beta\\
&= (e^{2\cdot0},2\cdot1e^{2\cdot 0})\cdot\frac{\vec{PQ}}{|PQ|}\\
&= (1,2)\cdot (\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})\\
&= -\frac{\sqrt{2}}{2}
\end{aligned}
$$
求 $f(x,y,z)=xy+yz+zx$ 在点 $(1,1,2)$ 沿方向 $l$ 的方向导数,其中 $l$ 的方向角分别为 $(60^\circ,45^\circ,60^\circ)$ 。
$$
\begin{aligned}
\frac{\partial f}{\partial l}\bigg|_{(1,0)}&=f_x^\prime(1,1,2)\cos\alpha+f_y^\prime(1,1,2)\cos\beta+f_z^\prime(1,1,2)\cos\gamma\\
&=\frac{5+3\sqrt{2}}{2}
\end{aligned}
$$
求函数 $u=x^2+y^2+z^2$ 在椭球面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ 上点 $M_0(x_0,y_0,z_0)$ 处沿外法线方向的方向导数。
椭球面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ 上点 $M_0(x_0,y_0,z_0)$ 处的法向量是 $\vec{n}=(\frac{2x_0}{a^2},\frac{2y_0}{b^2},\frac{2z_0}{c^2})$ ,因此 $u$ 在该点的方向导数为:
$$
\begin{aligned}
\frac{\partial u}{\partial l} &= \frac{\vec{n}}{|\vec{n}|}\cdot (2x_0,2y_0,2z_0)\\
&=\frac{1}{\sqrt{\frac{4x_0^2}{a^4}+\frac{4y_0^2}{b^4}+\frac{4z_0^2}{c^4}}}(\frac{4x_0^2}{a^2}+\frac{4y_0^2}{b^2}+\frac{4z_0^2}{c^2})\\
&=\frac{2}{\sqrt{\frac{x_0^2}{a^4}+\frac{y_0^2}{b^4}+\frac{z_0^2}{c^4}}}
\end{aligned}
$$
梯度
简单地说,曲面 $\Sigma:F(x,y,z)=0$ 上某一点 $P(x_0,y_0,z_0)$ 的梯度就是一个由偏导数构成的向量,三维情况下该向量就是:
$$
\textbf{grad}F(x_0,y_0,z_0)=\frac{\partial F}{\partial x}\vec{i}+\frac{\partial F}{\partial y}\vec{j}+\frac{\partial F}{\partial z}\vec{k}
$$
这个向量反应了:沿着梯度的方向,曲面上该点的方向导数最大。推导如下:
$$
\begin{aligned}
\frac{\partial F}{\partial l} &= (F_x^\prime,F_y^\prime,F_z^\prime)\cdot(\cos\alpha,\cos\beta,\cos\gamma)\\
&=|(F_x^\prime,F_y^\prime,F_z^\prime)|\cdot|\vec{e}|\cos\theta
\end{aligned}
$$
显然当 $\theta=0$ 时,方向导数取最大值,即方向向量和 $(F_x^\prime,F_y^\prime,F_z^\prime)$ 同方向。
求 $\textbf{grad}\frac{1}{x^2+y^2}$ 。
$\frac{-2x}{(x^2+y^2)^2}i+\frac{-2y}{(x^2+y^2)^2}j$ 。
多元函数极值
无条件极值
首先给出驻点的定义:使得 $f_x^\prime(x,y)=0,f_y^\prime(x,y)=0$ 同时成立的点 $(x,y)$ 称为函数 $f(x,y)$ 的驻点。
设函数 $f(x,y)$ 在点 $P(x_0,y_0)$ 的一阶偏导数存在,且在 $P$ 取得极值,则:
$$
f_x^\prime(x_0,y_0)=0,f_y^\prime(x_0,y_0)=0
$$
由此可见,极值点一定是驻点,但是驻点不一定是极值点。
设函数 $f(x,y)$ 在点 $(x_0,y_0)$ 的某邻域内由连续的二阶偏导数,且 $f_x^\prime(x_0,y_0)=0,f_y^\prime(x_0,y_0)=0$ 。令 $f_{xx}^{\prime\prime}(x_0,y_0)=A,f_{xy}^{\prime\prime}(x_0,y_0)=B,f_{yy}^{\prime\prime}(x_0,y_0)=C$ ,则:
- $AC-B^2\gt 0$ 时,$f(x,y)$ 在点 $(x_0,y_0)$ 取极值,且 $A\gt 0$ 时取极小值,$A\lt 0$ 时取极大值。
- $AC-B^2\lt 0$ 时,$f(x,y)$ 在点 $(x_0,y_0)$ 无极值。
- $AC-B^2= 0$ 时,不确定。可以用定义进一步讨论。
求 $f(x,y)=x^3-y^3+3x^2+3y^2-9x$ 的极值。
先求一阶偏导:$f_x^\prime=3x^2+6x-9,f_y^\prime=-3y^2+6y$ 。然后根据极值存在的必要条件求出所有驻点:$(1,0),(1,2),(-3,0),(-3,2)$ 。
最后求二阶偏导数,并进行极值点的判断:$A=f_{xx}^{\prime\prime}=6x+6,B=f_{xy}^{\prime\prime}=0,C=f_{yy}^{\prime\prime}=-6y+6$ 。
- 点 $(1,0)$:$AC-B^2\gt 0,A\gt 0$ ,因此是极小值点,极值为 $-5$。
- 点 $(1,2)$:$AC-B^2\lt 0$ ,不是极值点。
- 点 $(-3,0)$:$AC-B^2\lt 0$,不是极值点。
- 点 $(-3,2)$:$AC-B^2\gt 0,A\lt 0$,因此是极大值点,极值为 $31$。
条件极值
条件极值实际上就是函数 $f(x,y)$ 在条件 $\varphi(x,y)=0$ 下求极值,一般采用拉格朗日乘数法解决此类问题。
构造拉格朗日函数 $F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$ ,然后解方程组:
$$
\begin{cases}
\frac{\partial F}{\partial x}=\frac{\partial f}{\partial x}+\lambda\frac{\partial \varphi}{\partial x}=0\\
\frac{\partial F}{\partial y}=\frac{\partial f}{\partial y}+\lambda\frac{\partial \varphi}{\partial y}=0\\
\frac{\partial F}{\partial \lambda}=\varphi(x,y)=0
\end{cases}
$$
所有满足此方程组的解 $(x,y,\lambda)$ 中 $(x,y)$ 是函数 $f(x,y)$ 在条件 $\varphi(x,y)=0$ 下可能的极值点。
该方法是可以拓展的,比如函数 $f(x,y,z)$ 在条件 $\varphi(x,y,z)=0,\psi(x,y,z)=0$ 下的极值,我们可以构造拉格朗日函数 $F(x,y,z,\lambda,\mu)=f(x,y,z)+\lambda\varphi(x,y,z)+\mu\psi(x,y,z)$ ,然后也是解方程组,求出来的所有点都可能是极值点。
求函数 $u=x^2+y^2+z^2$ 在条件 $z=x^2+y^2,x+y+z=4$ 下的最大值和最小值。
令 $f(x,y,z)=x^2+y^2+z^2,\varphi(x,y,z)=x^2+y^2-z,\psi(x,y,z)=x+y+z-4$,然后构造拉格朗日函数:$F(x,y,z,\lambda,\mu)=f+\lambda\varphi+\mu\psi$ ,并求解方程组:
$$
\begin{cases}
\frac{\partial F}{\partial x}=2x+2\lambda x+\mu=0\\
\frac{\partial F}{\partial y}=2y+2\lambda y+\mu=0\\
\frac{\partial F}{\partial z}=2z-\lambda+\mu=0\\
\frac{\partial F}{\partial \lambda}=x^2+y^2-z=0\\
\frac{\partial F}{\partial \mu}=x+y+z-4=0
\end{cases}
$$
观察结构,容易发现式1减去式2可以得到关系:$(1+\lambda)(x-y)=0$ ,分类讨论后解出该方程组的解为 $(1,1,2)$ 和 $(-2,-2,8)$ ,因此最小值为 $6$,最大值为 $72$。
求平面 $\frac{x}{3}+\frac{y}{4}+\frac{z}{5}=1$ 和柱面 $x^2+y^2=1$ 的交线上与 $xOy$ 平面距离最短的点。
实际上就是已知两个约束条件:$\varphi:\frac{x}{3}+\frac{y}{4}+\frac{z}{5}-1=0$ 和 $\psi:x^2+y^2-1=0$ ,最小化 $|z|$ 。由于带绝对值的函数不方便,因此我们不妨最小化 $z^2$ 。
构造拉格朗日函数 $F=z^2+\lambda\varphi+\mu\psi$ ,并且列出方程组:
$$
\begin{cases}
\frac{\partial F}{\partial x}=\frac{\lambda}{3}+2\mu x=0\\
\frac{\partial F}{\partial y}=\frac{\lambda}{4}+2\mu y=0\\
\frac{\partial F}{\partial z}=2z+\frac{\lambda}{5}=0\\
\frac{x}{3}+\frac{y}{4}+\frac{z}{5}=1\\
x^2+y^2=1
\end{cases}
$$
注意式1和式2可以消元得到 $x,y$ 之间的关系,因此不难解出本题 $|z|_\min$ 时的坐标为 $(\frac{4}{5},\frac{3}{5},\frac{35}{12})$ 。即最短距离为 $\frac{35}{12}$ 。