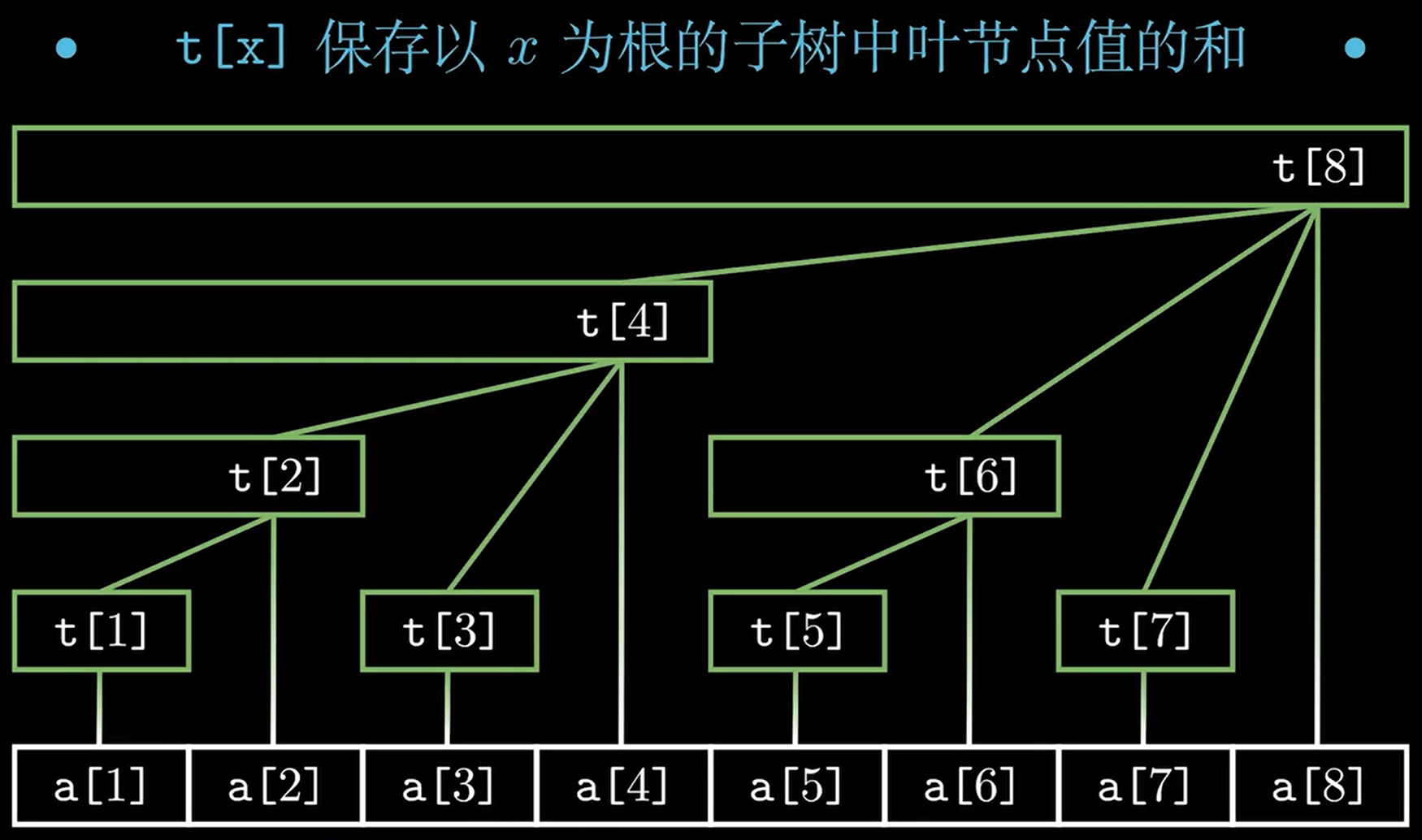
一般情况下，数据结构我们都以 $1$ 作为起始下标。

lowbit

$lowbit$ 操作是为了求出一个数字 $x$ 在二进制形态下，最低位的 $1$ 。

例如 $(110100)_2$ 中最低位 $1$ 的是 $(100)_2$ 。

$lowbit$ 求解的方法是，先将 $x$ 的二进制按位取反，然后 $+1$ ，再按位与原数字。

$lowbit$ 求解的方法是，先将 $x$ 的二进制按位取反，然后 $+1$ ，再和原数字按位与。例如：$(110100)_2$ ：

1. 按位取反 $(001011)_2$
2. $+1$ $(001100)_2$
3. 按位与原数 $(000100)_2$

由于计算机中负数采用补码存储，于是第一、二步的操作可以简化为 $\times (-1)$

树状数组每个单元 $t[i]$ 维护的东西本质上是 $a[i],a[i-1],\ldots,a[i-lowbit(i)+1]$ 这一段连续区间之和。比如 $lowbit(6)=2$ ，因此 $t[6]=a[6]+a[5]$ 。也就是说，$lowbit(x)$ 代表树状数组中第 $x$ 位元素覆盖的区间长度。

单点修改和区间查询

模板题：P3374 【模板】树状数组 1。

单点修改

这是最基础的树状数组操作，当原数组中第 $i$ 位元素加上 $x$ 后（$a[i] += x$），那么我们就需要向上跳，更新每一个覆盖到 $i$ 的区间。以顶部的图为例，假如现在现在更新了 $a[5]$ ，那么就需要更新树状数组中的 $t[5],t[6],t[8]$ 。

这里我们需要利用一个性质：在树状数组中，节点 $x$ 的父节点就是 $x+lowbit(x)$ 。然后就可以轻松写出单点修改的函数了：

// 以下代码，默认原数组为 a[]，树状数组为 t[]
void add(int pos, int x) { //pos位置加上x
    for (; pos <= n; pos += lowbit(pos)) { //n为数组大小
        t[pos] += x;
    }
}

区间查询

对于区间查询，我们容易联想到前缀和思想，求 $a[l]+a[l+1]+\cdots+a[r]$ 如果可以转化为 $pre[r]-pre[l-1]$ ，那么我们就可以解决区间查询问题了。

同时，由于树状数组的特性，我们是可以快速查询某一位置的前缀和的，比如要求 $pre[7]$ ，从顶部图片中我们可以发现 $pre[7]=t[7]+t[6]+t[4]$ ，这说明如果要求 $pre[x]$ 我们只需要每次减去 $lowbit(x)$ 向前跳即可，不难写出区间查询的函数：

int query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
    int res = 0;
    for (; pos > 0; pos -= lowbit(pos)) {
        res += tree[pos];
    }
    return res;
}

int sum(int l, int r) { // [l, r]区间查询
    return query(r) - query(l - 1);
}

很显然，单点修改和区间查询的复杂度都是 $O(\log N)$ 量级的（一个简单的证明：每一次加上/减去的$lowbit(x)$ 至少扩大 $2$ 倍）。

模板题AC代码如下：

#include <bits/stdc++.h>
using namespace std;

template<typename T> struct fenwickTree {
    int n, hbit;
    vector<T> tree;
    fenwickTree(int n_ = 0) : n(n_), tree(n_ + 1), hbit(log2(n_) + 1) {}
    int lowbit(int x) { return x & (-x); }
    int size() { return n; }
    void add(int pos, int x) { // pos位置加上x
        for (; pos <= n; pos += lowbit(pos)) {
            tree[pos] += x;
        }
    }
    T query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
        T res = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            res += tree[pos];
        }
        return res;
    }
    T sum(int l, int r) { // [l, r]区间查询
        return query(r) - query(l - 1);
    }
    int kth(int k) { // 第k大元素
        int ans = 0, cnt = 0;
        for (int i = hbit; i >= 0; i--) {
            ans += (1 << i);
            if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
            else cnt += tree[ans];
        }
        return ++ans;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n, m;
    cin >> n >> m;
    fenwickTree<long long> fwt(n);
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        fwt.add(i + 1, x);
    }
    for (int i = 0; i < m; i++) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            fwt.add(x, y);
        } else {
            cout << fwt.sum(x, y) << "\n";
        }
    }
    return 0;
}

区间修改和单点查询

模板题：P3368 【模板】树状数组 2。

差分思想

首先介绍一下差分思想，我们看下面这个弱化版的例题：

给定一个大小为 $N$ 的数组 $A$ ，$M$ 次操作，每次操作都会指定一个区间 $[L_i, R_i]$ 加上 $X_i$ 。询问最终的数组 $A$ 。

$N,M=10^6$ 。

本题可以直接用差分思想解决，而不需要任何数据结构，只需要构造一个数组 $B$ 并满足：

$$
\begin{cases}
B_i=A_i-A_{i-1} & i>0\\
B_i=A_i & i=0
\end{cases}
$$

可以注意到一个点：数组 $B$ 的前缀和满足： $pre_B[i]=A[i]$ ，因此我们可以通过维护数组 $B$ 求出数组 $A$ 。

更具体地，由于区间加并不会影响差分数组的中间项，于是我们只需要修改 $B[L],B[R+1]$ ：$B[L]+=X,B[R+1]-=X$ 。完成所有区间加之后，对差分数组求一个前缀和就是答案了。

区间修改

树状数组可以通过差分思想来实现区间修改的操作：我们建树状数组的时候不再是以 $a$ 数组建树，而是以差分数组 $b$ 建树（$b_i=a_i-a_{i-1}$）。

此时，我们对树状数组上某一点 $x$ 进行单点询问的话，本质上就是在计算 $a[x]$ （对差分数组求前缀和就是原数组单点求值）。同时，由于区间修改在差分数组中就是做两个单点修改，因此我们只需要像上面一样进行两个单点的更新：$b[l]+=x, b[r+1]-=x$ 。

于是就可以写出区间修改+单点更新的代码了：

#include <bits/stdc++.h>
using namespace std;

template<typename T> struct fenwickTree {
    int n, hbit;
    vector<T> tree;
    fenwickTree(int n_ = 0) : n(n_), tree(n_ + 1), hbit(log2(n_) + 1) {}
    int lowbit(int x) { return x & (-x); }
    int size() { return n; }
    void add(int pos, int x) { // pos位置加上x
        for (; pos <= n; pos += lowbit(pos)) {
            tree[pos] += x;
        }
    }
    T query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
        T res = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            res += tree[pos];
        }
        return res;
    }
    T sum(int l, int r) { // [l, r]区间查询
        return query(r) - query(l - 1);
    }
    int kth(int k) { // 第k大元素
        int ans = 0, cnt = 0;
        for (int i = hbit; i >= 0; i--) {
            ans += (1 << i);
            if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
            else cnt += tree[ans];
        }
        return ++ans;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n, m;
    cin >> n >> m;
    vector<int> a(n), b(n);
    fenwickTree<long long> fwt(n + 1);
    for (auto& i : a) {
        cin >> i;
    }
    adjacent_difference(a.begin(), a.end(), b.begin());
    for (int i = 0; i < n; i++) {
        fwt.add(i + 1, b[i]);
    }
    for (int i = 0; i < m; i++) {
        int op, x, y, k;
        cin >> op >> x;
        if (op == 1) {
            cin >> y >> k;
            fwt.add(x, k);
            fwt.add(y + 1, -k);
        } else {
            cout << fwt.query(x) << "\n";
        }
    }
    return 0;
}

区间修改和区间查询

模板题：P3372 【模板】线段树 1。

如果遇到区间修改+区间查询的话，一般我们都会考虑直接用线段树了，但实际上树状数组也是可以做到的。

区间查询

首先，我们还是像区间修改+单点查询那样维护差分数组。对于某个区间 $[l,r]$ 的查询，还是利用前缀和思想变成两个单点询问：$pre[r]-pre[l-1]$ 。不过由于树状数组现在维护的是差分数组 $b$ ，因此对某个位置 $x$ 的前缀和询问变成了：

$$
pre[x]=\sum_{i=1}^x\sum_{j=1}^i b[j]
$$

这个式子显然是不能硬算的，我们还需要变形（这个变形从几何角度理解更好，可以参考这个视频4：59开始的内容）：

$$
\sum_{i=1}^x\sum_{j=1}^i b[j]=(x+1)\sum_{i=1}^{x}b[i]-\sum_{i=1}^{x}i\times b[i]
$$

上式中 $(x+1)\sum_{i=1}^{x}b[i]$ 显然可以直接单点查询来实现，而后面的 $\sum_{i=1}^{x}i\times b[i]$ 可以再开一个树状数组来维护。（因为 $ib[i]$ 也可以用差分数组维护）因此，我们可以开两个树状数组实现区间修改+区间查询。

代码如下：

#include <bits/stdc++.h>
using namespace std;

template<typename T> struct fenwickTree {
    int n, hbit;
    vector<T> tree;
    fenwickTree(int n_ = 0) : n(n_), tree(n_ + 1), hbit(log2(n_) + 1) {}
    int lowbit(int x) { return x & (-x); }
    int size() { return n; }
    void add(int pos, long long x) { // pos位置加上x
        for (; pos <= n; pos += lowbit(pos)) {
            tree[pos] += x;
        }
    }
    T query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
        T res = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            res += tree[pos];
        }
        return res;
    }
    T sum(int l, int r) { // [l, r]区间查询
        return query(r) - query(l - 1);
    }
    int kth(int k) { // 第k大元素
        int ans = 0, cnt = 0;
        for (int i = hbit; i >= 0; i--) {
            ans += (1 << i);
            if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
            else cnt += tree[ans];
        }
        return ++ans;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n, m;
    cin >> n >> m;
    vector<long long> a(n), b(n);
    fenwickTree<long long> fwt1(n + 1), fwt2(n + 1);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    adjacent_difference(a.begin(), a.end(), b.begin());
    for (int i = 0; i < n; i++) {
        fwt1.add(i + 1, b[i]);
        fwt2.add(i + 1, 1LL * (i + 1) * b[i]);
    }
    for (int i = 0; i < m; i++) {
        int op, x, y, k;
        cin >> op >> x >> y;
        if (op == 1) {
            cin >> k;
            fwt1.add(x, k);
            fwt1.add(y + 1, -k);
            fwt2.add(x, 1LL * k * x);
            fwt2.add(y + 1, 1LL * -k * (y + 1));
        } else {
            long long left = 1LL * (x) * fwt1.query(x - 1) - fwt2.query(x - 1);
            long long right = 1LL * (y + 1) * fwt1.query(y) - fwt2.query(y);
            cout << right - left << "\n";
        }
    }
    return 0;
}

倍增第k大

模板题：P3369 【模板】普通平衡树。

在可以离线操作的情况下，树状数组甚至可以用来替代平衡树求第k大的功能。

树状数组倍增

树状数组求第 $k$ 大元素显然可以用二分查询，但是这样的话复杂度就是 $O(\log^2 N)$ ，如果我们采用倍增的方法就可以将复杂度降为 $O(\log N)$ 。

具体做法是：利用树状数组的二进制特性，先从一个超过树状数组可表示范围的单元开始（比如树状数组的表示范围是 $N$ ，那我们就至少要从超过 $N$ 的最小的 $2^k$ 开始），检查向右跳 $2^k$ 步之后前缀和是否超过了 $k$，如果超过了就不跳，没超过就向右跳……直到找到第k大元素为止。这个做法说白了就是利用了lowbit的二进制特征，结合倍增跳跃正好就是再求前缀和。

函数如下：

int kth(int k) { // 第k大元素
    int ans = 0, cnt = 0;
    for (int i = hbit; i >= 0; i--) { // hbit就是超过N的最小的2^hbit
        ans += (1 << i);
        if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
        else cnt += tree[ans];
    }
    return ++ans;
}

普通平衡树AC代码：

#include <bits/stdc++.h>
using namespace std;
template<typename T> struct fenwickTree {
    int n, hbit;
    vector<T> tree;
    fenwickTree(int n_ = 0) : n(n_), tree(n_ + 1), hbit(log2(n_) + 1) {}
    int lowbit(int x) { return x & (-x); }
    int size() { return n; }
    void add(int pos, int x) { // pos位置加上x
        for (; pos <= n; pos += lowbit(pos)) {
            tree[pos] += x;
        }
    }
    T query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
        T res = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            res += tree[pos];
        }
        return res;
    }
    T sum(int l, int r) { // [l, r]区间查询
        return query(r) - query(l - 1);
    }
    int kth(int k) { // 第k大元素
        int ans = 0, cnt = 0;
        for (int i = hbit; i >= 0; i--) {
            ans += (1 << i);
            if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
            else cnt += tree[ans];
        }
        return ++ans;
    }
};
fenwickTree<int> fwt(200000);

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n;
    cin >> n;
    vector<pair<int, int>> p(n);
    vector<int> b, c(n + 1);
    for (auto& [x, y] : p) {
        cin >> x >> y;
        if (x != 4) {
            b.push_back(y);
        }
    }
    sort(b.begin(), b.end());
    b.erase(unique(b.begin(), b.end()), b.end());
    for (auto& [x, y] : p) {
        int z = y;
        if (x != 4) {
            y = lower_bound(b.begin(), b.end(), y) - b.begin() + 1;
            c[y] = z;
        }
        if (x == 1) {
            fwt.add(y, 1);
        } else if (x == 2) {
            fwt.add(y, -1);
        } else if (x == 3) {
            cout << fwt.query(y - 1) + 1 << "\n";
        } else if (x == 4) {
            cout << c[fwt.kth(y)] << "\n";
        } else if (x == 5) {
            cout << c[fwt.kth(fwt.query(y - 1))] << "\n";
        } else {
            cout << c[fwt.kth(fwt.query(y) + 1)] << "\n";
        }
    }
    return 0;
}

一些应用

逆序对

模板题：P1908 逆序对。

求逆序对基本上都采用这两种方法之一：树状数组和归并排序。在这里，我们说明一下树状数组怎么实现求解逆序对：

在这个模板题中，我们首先对所有元素离散化，然后再对这个新的数组（一个 $1,2,\ldots,N$ 的排列）建立权值树状数组进行逆序对的计算。主要的思路是：根据时序关系，每当我们遍历到一个数字 $x$ 时，该数字会与所有在它左侧（从时序角度来说，就是之前的所有元素）并且 $\ge x$ 的元素构成逆序对，因此我们只需要求区间 $[x+1,N]$ 中已有几个元素即可。

#include <bits/stdc++.h>
using namespace std;

template<typename T> struct fenwickTree {
    int n, hbit;
    vector<T> tree;
    fenwickTree(int n_ = 0) : n(n_), tree(n_ + 1), hbit(log2(n_) + 1) {}
    int lowbit(int x) { return x & (-x); }
    int size() { return n; }
    void add(int pos, int x) { // pos位置加上x
        for (; pos <= n; pos += lowbit(pos)) {
            tree[pos] += x;
        }
    }
    T query(int pos) { // 查询pos位置的前缀和 即a[1] + a[2] + ... + a[pos]
        T res = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            res += tree[pos];
        }
        return res;
    }
    T sum(int l, int r) { // [l, r]区间查询
        return query(r) - query(l - 1);
    }
    int kth(int k) { // 第k大元素
        int ans = 0, cnt = 0;
        for (int i = hbit; i >= 0; i--) {
            ans += (1 << i);
            if (ans > n || cnt + tree[ans] >= k) ans -= (1 << i);
            else cnt += tree[ans];
        }
        return ++ans;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n;
    cin >> n;
    vector<int> a(n);
    for (auto& i : a) {
        cin >> i;
    }
    auto p = a;
    sort(p.begin(), p.end());
    p.erase(unique(p.begin(), p.end()), p.end());
    for (auto& i : a) {
        i = lower_bound(p.begin(), p.end(), i) - p.begin() + 1;
    }
    fenwickTree<int> fwt(p.size() + 1);
    long long res = 0;
    for (int i = 0; i < n; i++) {
        fwt.add(a[i], 1);
        res += i + 1 - fwt.query(a[i]);
    }
    cout << res << "\n";
    return 0;
}

康托展开

模板题：P5367 【模板】康托展开。

康托展开可以用来求一个 ​$\{1,2,3,\ldots,N\}$ 的任意排列的排名（字典序排名）。

公式如下：

$$
\begin{aligned}
&\text{rank}=1+\sum_{i=1}^nA[i]\times(n-i)! \
&其中，A[i]=\sum^n_{j=i}[a[j]<a[i]]
\end{aligned}
$$

显然有了公式之后，就是求一下逆序对。